Spacetime
| Part of a series on |
| Spacetime |
|---|
 |
In physics, spacetime is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualizing and understanding relativistic effects such as how different observers perceive where and when events occur.
Until the turn of the 20th century, the assumption had been that the three-dimensional geometry of the universe (its description in terms of locations, shapes, distances, and directions) was distinct from time (the measurement of when events occur within the universe). However, space and time took on new meanings with the Lorentz transformation and special theory of relativity.
In 1908, Hermann Minkowski presented a geometric interpretation of special relativity that fused time and the three spatial dimensions of space into a single four-dimensional continuum now known as Minkowski space. This interpretation proved vital to the general theory of relativity, wherein spacetime is curved by mass and energy.
Fundamentals[edit]
Definitions[edit]
Non-relativistic classical mechanics treats time as a universal quantity of measurement which is uniform throughout space, and separate from space. Classical mechanics assumes that time has a constant rate of passage, independent of the observer's state of motion, or anything external.[1] It assumes that space is Euclidean: it assumes that space follows the geometry of common sense.[2]
In the context of special relativity, time cannot be separated from the three dimensions of space, because the observed rate at which time passes for an object depends on the object's velocity relative to the observer.[3]: 214–217 General relativity provides an explanation of how gravitational fields can slow the passage of time for an object as seen by an observer outside the field.
In ordinary space, a position is specified by three numbers, known as dimensions. In the Cartesian coordinate system, these are called x, y, and z. A position in spacetime is called an event, and requires four numbers to be specified: the three-dimensional location in space, plus the position in time (Fig. 1). An event is represented by a set of coordinates x, y, z and t.[4] Spacetime is thus four-dimensional.
Unlike the analogies used in popular writings to explain events, such as firecrackers or sparks, mathematical events have zero duration and represent a single point in spacetime.[5] Although it is possible to be in motion relative to the popping of a firecracker or a spark, it is not possible for an observer to be in motion relative to an event.
The path of a particle through spacetime can be considered to be a succession of events. The series of events can be linked together to form a line which represents a particle's progress through spacetime. That line is called the particle's world line.[6]: 105
Mathematically, spacetime is a manifold, which is to say, it appears locally "flat" near each point in the same way that, at small enough scales, the surface of a globe appears flat.[7] A scale factor, (conventionally called the speed-of-light) relates distances measured in space with distances measured in time. The magnitude of this scale factor (nearly 300,000 kilometres or 190,000 miles in space being equivalent to one second in time), along with the fact that spacetime is a manifold, implies that at ordinary, non-relativistic speeds and at ordinary, human-scale distances, there is little that humans might observe which is noticeably different from what they might observe if the world were Euclidean. It was only with the advent of sensitive scientific measurements in the mid-1800s, such as the Fizeau experiment and the Michelson–Morley experiment, that puzzling discrepancies began to be noted between observation versus predictions based on the implicit assumption of Euclidean space.[8]

In special relativity, an observer will, in most cases, mean a frame of reference from which a set of objects or events is being measured. This usage differs significantly from the ordinary English meaning of the term. Reference frames are inherently nonlocal constructs, and according to this usage of the term, it does not make sense to speak of an observer as having a location.[9]
In Fig. 1-1, imagine that the frame under consideration is equipped with a dense lattice of clocks, synchronized within this reference frame, that extends indefinitely throughout the three dimensions of space. Any specific location within the lattice is not important. The latticework of clocks is used to determine the time and position of events taking place within the whole frame. The term observer refers to the whole ensemble of clocks associated with one inertial frame of reference.[9]: 17–22
In this idealized case, every point in space has a clock associated with it, and thus the clocks register each event instantly, with no time delay between an event and its recording. A real observer, will see a delay between the emission of a signal and its detection due to the speed of light. To synchronize the clocks, in the data reduction following an experiment, the time when a signal is received will be corrected to reflect its actual time were it to have been recorded by an idealized lattice of clocks.[9]: 17–22
In many books on special relativity, especially older ones, the word "observer" is used in the more ordinary sense of the word. It is usually clear from context which meaning has been adopted.
Physicists distinguish between what one measures or observes, after one has factored out signal propagation delays, versus what one visually sees without such corrections. Failure to understand the difference between what one measures/observes versus what one sees is the source of much error among beginning students of relativity.[10]
History[edit]
By the mid-1800s, various experiments such as the observation of the Arago spot and differential measurements of the speed of light in air versus water were considered to have proven the wave nature of light as opposed to a corpuscular theory.[11] Propagation of waves was then assumed to require the existence of a waving medium; in the case of light waves, this was considered to be a hypothetical luminiferous aether.[note 1] The various attempts to establish the properties of this hypothetical medium yielded contradictory results. For example, the Fizeau experiment of 1851, conducted by French physicist Hippolyte Fizeau, demonstrated that the speed of light in flowing water was less than the sum of the speed of light in air plus the speed of the water by an amount dependent on the water's index of refraction.[12]
Among other issues, the dependence of the partial aether-dragging implied by this experiment on the index of refraction (which is dependent on wavelength) led to the unpalatable conclusion that aether simultaneously flows at different speeds for different colors of light.[13] The famous Michelson–Morley experiment of 1887 (Fig. 1-2) showed no differential influence of Earth's motions through the hypothetical aether on the speed of light, and the most likely explanation, complete aether dragging, was in conflict with the observation of stellar aberration.[8]
George Francis FitzGerald in 1889,[14] and Hendrik Lorentz in 1892, independently proposed that material bodies traveling through the fixed aether were physically affected by their passage, contracting in the direction of motion by an amount that was exactly what was necessary to explain the negative results of the Michelson–Morley experiment. No length changes occur in directions transverse to the direction of motion.
By 1904, Lorentz had expanded his theory such that he had arrived at equations formally identical with those that Einstein was to derive later, i.e. the Lorentz transformation.[15] As a theory of dynamics (the study of forces and torques and their effect on motion), his theory assumed actual physical deformations of the physical constituents of matter.[16]: 163–174 Lorentz's equations predicted a quantity that he called local time, with which he could explain the aberration of light, the Fizeau experiment and other phenomena.
Henri Poincaré was the first to combine space and time into spacetime.[17][18]: 73–80, 93–95 He argued in 1898 that the simultaneity of two events is a matter of convention.[19][note 2] In 1900, he recognized that Lorentz's "local time" is actually what is indicated by moving clocks by applying an explicitly operational definition of clock synchronization assuming constant light speed.[note 3] In 1900 and 1904, he suggested the inherent undetectability of the aether by emphasizing the validity of what he called the principle of relativity. In 1905/1906[20] he mathematically perfected Lorentz's theory of electrons in order to bring it into accordance with the postulate of relativity.
While discussing various hypotheses on Lorentz invariant gravitation, he introduced the innovative concept of a 4-dimensional spacetime by defining various four vectors, namely four-position, four-velocity, and four-force.[21][22] He did not pursue the 4-dimensional formalism in subsequent papers, however, stating that this line of research seemed to "entail great pain for limited profit", ultimately concluding "that three-dimensional language seems the best suited to the description of our world".[22] Even as late as 1909, Poincaré continued to describe the dynamical interpretation of the Lorentz transform.[16]: 163–174
In 1905, Albert Einstein analyzed special relativity in terms of kinematics (the study of moving bodies without reference to forces) rather than dynamics. His results were mathematically equivalent to those of Lorentz and Poincaré. He obtained them by recognizing that the entire theory can be built upon two postulates: the principle of relativity and the principle of the constancy of light speed. His work was filled with vivid imagery involving the exchange of light signals between clocks in motion, careful measurements of the lengths of moving rods, and other such examples.[23][note 4]
Einstein in 1905 superseded previous attempts of an electromagnetic mass–energy relation by introducing the general equivalence of mass and energy, which was instrumental for his subsequent formulation of the equivalence principle in 1907, which declares the equivalence of inertial and gravitational mass. By using the mass–energy equivalence, Einstein showed that the gravitational mass of a body is proportional to its energy content, which was one of the early results in developing general relativity. While it would appear that he did not at first think geometrically about spacetime,[3]: 219 in the further development of general relativity, Einstein fully incorporated the spacetime formalism.
When Einstein published in 1905, another of his competitors, his former mathematics professor Hermann Minkowski, had also arrived at most of the basic elements of special relativity. Max Born recounted a meeting he had made with Minkowski, seeking to be Minkowski's student/collaborator:[25]
I went to Cologne, met Minkowski and heard his celebrated lecture 'Space and Time' delivered on 2 September 1908. [...] He told me later that it came to him as a great shock when Einstein published his paper in which the equivalence of the different local times of observers moving relative to each other was pronounced; for he had reached the same conclusions independently but did not publish them because he wished first to work out the mathematical structure in all its splendor. He never made a priority claim and always gave Einstein his full share in the great discovery.
Minkowski had been concerned with the state of electrodynamics after Michelson's disruptive experiments at least since the summer of 1905, when Minkowski and David Hilbert led an advanced seminar attended by notable physicists of the time to study the papers of Lorentz, Poincaré et al. Minkowski saw Einstein's work as an extension of Lorentz's, and was most directly influenced by Poincaré.[26]
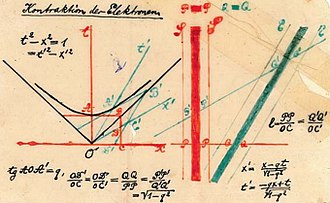
On 5 November 1907 (a little more than a year before his death), Minkowski introduced his geometric interpretation of spacetime in a lecture to the Göttingen Mathematical society with the title, The Relativity Principle (Das Relativitätsprinzip).[note 5] On 21 September 1908, Minkowski presented his famous talk, Space and Time (Raum und Zeit),[27] to the German Society of Scientists and Physicians. The opening words of Space and Time include Minkowski's famous statement that "Henceforth, space for itself, and time for itself shall completely reduce to a mere shadow, and only some sort of union of the two shall preserve independence." Space and Time included the first public presentation of spacetime diagrams (Fig. 1-4), and included a remarkable demonstration that the concept of the invariant interval (discussed below), along with the empirical observation that the speed of light is finite, allows derivation of the entirety of special relativity.[note 6]
The spacetime concept and the Lorentz group are closely connected to certain types of sphere, hyperbolic, or conformal geometries and their transformation groups already developed in the 19th century, in which invariant intervals analogous to the spacetime interval are used.[note 7]
Einstein, for his part, was initially dismissive of Minkowski's geometric interpretation of special relativity, regarding it as überflüssige Gelehrsamkeit (superfluous learnedness). However, in order to complete his search for general relativity that started in 1907, the geometric interpretation of relativity proved to be vital. In 1916, Einstein fully acknowledged his indebtedness to Minkowski, whose interpretation greatly facilitated the transition to general relativity.[16]: 151–152 Since there are other types of spacetime, such as the curved spacetime of general relativity, the spacetime of special relativity is today known as Minkowski spacetime.
Spacetime in special relativity[edit]
Spacetime interval[edit]
In three dimensions, the distance between two points can be defined using the Pythagorean theorem:
Although two viewers may measure the x, y, and z position of the two points using different coordinate systems, the distance between the points will be the same for both, assuming that they are measuring using the same units. The distance is "invariant".
In special relativity, however, the distance between two points is no longer the same if measured by two different observers, when one of the observers is moving, because of Lorentz contraction. The situation is even more complicated if the two points are separated in time as well as in space. For example, if one observer sees two events occur at the same place, but at different times, a person moving with respect to the first observer will see the two events occurring at different places, because, from their point of view, they are stationary, and the position of the event is receding or approaching. Thus, a different measure must be used to measure the effective "distance" between two events.[31]: 48–50, 100–102
In four-dimensional spacetime, the analog to distance is the interval. Although time comes in as a fourth dimension, it is treated differently than the spatial dimensions. Minkowski space hence differs in important respects from four-dimensional Euclidean space. The fundamental reason for merging space and time into spacetime is that space and time are separately not invariant, which is to say that, under the proper conditions, different observers will disagree on the length of time between two events (because of time dilation) or the distance between the two events (because of length contraction). Special relativity provides a new invariant, called the spacetime interval, which combines distances in space and in time. All observers who measure the time and distance between any two events will end up computing the same spacetime interval. Suppose an observer measures two events as being separated in time by and a spatial distance Then the squared spacetime interval between the two events that are separated by a distance in space and by in the -coordinate is:[32]
or for three space dimensions,
The constant the speed of light, converts time units (like seconds) into space units (like meters). The squared interval is a measure of separation between events A and B that are time separated and in addition space separated either because there are two separate objects undergoing events, or because a single object in space is moving inertially between its events. The separation interval is derived by squaring the spatial distance separating event B from event A and subtracting it from the square of the spatial distance traveled by a light signal in that same time interval . If the event separation is due to a light signal, then this difference vanishes and .
When the event considered is infinitesimally close to each other, then we may write
In a different inertial frame, say with coordinates , the spacetime interval can be written in a same form as above. Because of the constancy of speed of light, the light events in all inertial frames belong to zero interval, . For any other infinitesimal event where , one can prove that which in turn upon integration leads to .[33]: 2 The invariance of interval of any event between all intertial frames of reference is one of the fundamental results of special theory of relativity.
Although for brevity, one frequently sees interval expressions expressed without deltas, including in most of the following discussion, it should be understood that in general, means , etc. We are always concerned with differences of spatial or temporal coordinate values belonging to two events, and since there is no preferred origin, single coordinate values have no essential meaning.

The equation above is similar to the Pythagorean theorem, except with a minus sign between the and the terms. The spacetime interval is the quantity not itself. The reason is that unlike distances in Euclidean geometry, intervals in Minkowski spacetime can be negative. Rather than deal with square roots of negative numbers, physicists customarily regard as a distinct symbol in itself, rather than the square of something.[3]: 217
- Note: There are two sign conventions in use in the relativity literature:
- and
- These sign conventions are associated with the metric signatures (+−−−) and (−+++). A minor variation is to place the time coordinate last rather than first. Both conventions are widely used within the field of study.[34]
- In the following discussion, we use the first convention.
In general can assume any real number value. If is positive, the spacetime interval is referred to as timelike. Since spatial distance traversed by any massive object is always less than distance traveled by the light for the same time interval, positive intervals are always timelike. If is negative, the spacetime interval is said to be spacelike. Spacetime intervals are equal to zero when In other words, the spacetime interval between two events on the world line of something moving at the speed of light is zero. Such an interval is termed lightlike or null. A photon arriving in our eye from a distant star will not have aged, despite having (from our perspective) spent years in its passage.[31]: 48–50
A spacetime diagram is typically drawn with only a single space and a single time coordinate. Fig. 2-1 presents a spacetime diagram illustrating the world lines (i.e. paths in spacetime) of two photons, A and B, originating from the same event and going in opposite directions. In addition, C illustrates the world line of a slower-than-light-speed object. The vertical time coordinate is scaled by so that it has the same units (meters) as the horizontal space coordinate. Since photons travel at the speed of light, their world lines have a slope of ±1.[31]: 23–25 In other words, every meter that a photon travels to the left or right requires approximately 3.3 nanoseconds of time.
Reference frames[edit]
This section needs additional citations for verification. (March 2024) |
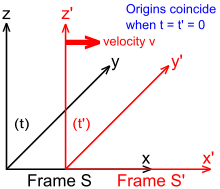
To gain insight in how spacetime coordinates measured by observers in different reference frames compare with each other, it is useful to work with a simplified setup with frames in a standard configuration. With care, this allows simplification of the math with no loss of generality in the conclusions that are reached. In Fig. 2-2, two Galilean reference frames (i.e. conventional 3-space frames) are displayed in relative motion. Frame S belongs to a first observer O, and frame S′ (pronounced "S prime") belongs to a second observer O′.
- The x, y, z axes of frame S are oriented parallel to the respective primed axes of frame S′.
- Frame S′ moves in the x-direction of frame S with a constant velocity v as measured in frame S.
- The origins of frames S and S′ are coincident when time t = 0 for frame S and t′ = 0 for frame S′.[6]: 107
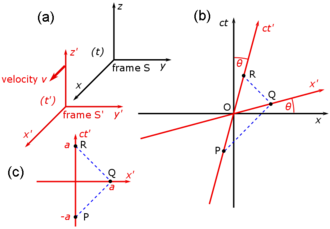
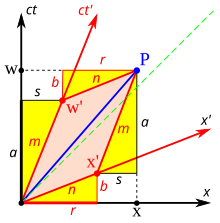
Fig. 2-3a redraws Fig. 2-2 in a different orientation. Fig. 2-3b illustrates a relativistic spacetime diagram from the viewpoint of observer O. Since S and S′ are in standard configuration, their origins coincide at times t = 0 in frame S and t′ = 0 in frame S′. The ct′ axis passes through the events in frame S′ which have x′ = 0. But the points with x′ = 0 are moving in the x-direction of frame S with velocity v, so that they are not coincident with the ct axis at any time other than zero. Therefore, the ct′ axis is tilted with respect to the ct axis by an angle θ given by[31]: 23–31
The x′ axis is also tilted with respect to the x axis. To determine the angle of this tilt, we recall that the slope of the world line of a light pulse is always ±1. Fig. 2-3c presents a spacetime diagram from the viewpoint of observer O′. Event P represents the emission of a light pulse at x′ = 0, ct′ = −a. The pulse is reflected from a mirror situated a distance a from the light source (event Q), and returns to the light source at x′ = 0, ct′ = a (event R).
The same events P, Q, R are plotted in Fig. 2-3b in the frame of observer O. The light paths have slopes = 1 and −1, so that △PQR forms a right triangle with PQ and QR both at 45 degrees to the x and ct axes. Since OP = OQ = OR, the angle between x′ and x must also be θ.[6]: 113–118
While the rest frame has space and time axes that meet at right angles, the moving frame is drawn with axes that meet at an acute angle. The frames are actually equivalent.[31]: 23–31 The asymmetry is due to unavoidable distortions in how spacetime coordinates can map onto a Cartesian plane, and should be considered no stranger than the manner in which, on a Mercator projection of the Earth, the relative sizes of land masses near the poles (Greenland and Antarctica) are highly exaggerated relative to land masses near the Equator.
Light cone[edit]

In Fig. 2–4, event O is at the origin of a spacetime diagram, and the two diagonal lines represent all events that have zero spacetime interval with respect to the origin event. These two lines form what is called the light cone of the event O, since adding a second spatial dimension (Fig. 2-5) makes the appearance that of two right circular cones meeting with their apices at O. One cone extends into the future (t>0), the other into the past (t<0).

A light (double) cone divides spacetime into separate regions with respect to its apex. The interior of the future light cone consists of all events that are separated from the apex by more time (temporal distance) than necessary to cross their spatial distance at lightspeed; these events comprise the timelike future of the event O. Likewise, the timelike past comprises the interior events of the past light cone. So in timelike intervals Δct is greater than Δx, making timelike intervals positive.[3]: 220
The region exterior to the light cone consists of events that are separated from the event O by more space than can be crossed at lightspeed in the given time. These events comprise the so-called spacelike region of the event O, denoted "Elsewhere" in Fig. 2-4. Events on the light cone itself are said to be lightlike (or null separated) from O. Because of the invariance of the spacetime interval, all observers will assign the same light cone to any given event, and thus will agree on this division of spacetime.[3]: 220
The light cone has an essential role within the concept of causality. It is possible for a not-faster-than-light-speed signal to travel from the position and time of O to the position and time of D (Fig. 2-4). It is hence possible for event O to have a causal influence on event D. The future light cone contains all the events that could be causally influenced by O. Likewise, it is possible for a not-faster-than-light-speed signal to travel from the position and time of A, to the position and time of O. The past light cone contains all the events that could have a causal influence on O. In contrast, assuming that signals cannot travel faster than the speed of light, any event, like e.g. B or C, in the spacelike region (Elsewhere), cannot either affect event O, nor can they be affected by event O employing such signalling. Under this assumption any causal relationship between event O and any events in the spacelike region of a light cone is excluded.[35]
Relativity of simultaneity[edit]
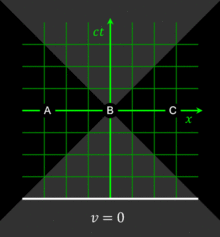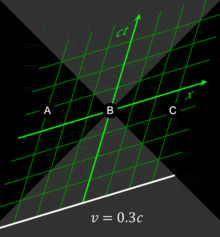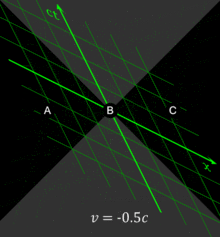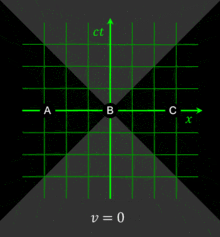
All observers will agree that for any given event, an event within the given event's future light cone occurs after the given event. Likewise, for any given event, an event within the given event's past light cone occurs before the given event. The before–after relationship observed for timelike-separated events remains unchanged no matter what the reference frame of the observer, i.e. no matter how the observer may be moving. The situation is quite different for spacelike-separated events. Fig. 2-4 was drawn from the reference frame of an observer moving at v = 0. From this reference frame, event C is observed to occur after event O, and event B is observed to occur before event O.[36]
From a different reference frame, the orderings of these non-causally-related events can be reversed. In particular, one notes that if two events are simultaneous in a particular reference frame, they are necessarily separated by a spacelike interval and thus are noncausally related. The observation that simultaneity is not absolute, but depends on the observer's reference frame, is termed the relativity of simultaneity.[36]
Fig. 2-6 illustrates the use of spacetime diagrams in the analysis of the relativity of simultaneity. The events in spacetime are invariant, but the coordinate frames transform as discussed above for Fig. 2-3. The three events (A, B, C) are simultaneous from the reference frame of an observer moving at v = 0. From the reference frame of an observer moving at v = 0.3c, the events appear to occur in the order C, B, A. From the reference frame of an observer moving at v = −0.5c, the events appear to occur in the order A, B, C. The white line represents a plane of simultaneity being moved from the past of the observer to the future of the observer, highlighting events residing on it. The gray area is the light cone of the observer, which remains invariant.
A spacelike spacetime interval gives the same distance that an observer would measure if the events being measured were simultaneous to the observer. A spacelike spacetime interval hence provides a measure of proper distance, i.e. the true distance = Likewise, a timelike spacetime interval gives the same measure of time as would be presented by the cumulative ticking of a clock that moves along a given world line. A timelike spacetime interval hence provides a measure of the proper time = [3]: 220–221
Invariant hyperbola[edit]
This section needs additional citations for verification. (March 2024) |
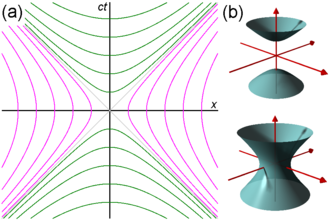
In Euclidean space (having spatial dimensions only), the set of points equidistant (using the Euclidean metric) from some point form a circle (in two dimensions) or a sphere (in three dimensions). In (1+1)-dimensional Minkowski spacetime (having one temporal and one spatial dimension), the points at some constant spacetime interval away from the origin (using the Minkowski metric) form curves given by the two equations
with some positive real constant. These equations describe two families of hyperbolae in an x–ct spacetime diagram, which are termed invariant hyperbolae.
In Fig. 2-7a, each magenta hyperbola connects all events having some fixed spacelike separation from the origin, while the green hyperbolae connect events of equal timelike separation.
The magenta hyperbolae, which cross the x axis, are timelike curves, which is to say that these hyperbolae represent actual paths that can be traversed by (constantly accelerating) particles in spacetime: Between any two events on one hyperbola a causality relation is possible, because the inverse of the slope—representing the necessary speed—for all secants is less than . On the other hand, the green hyperbolae, which cross the ct axis, are spacelike curves because all intervals along these hyperbolae are spacelike intervals: No causality is possible between any two points on one of these hyperbolae, because all secants represent speeds larger than .
Fig. 2-7b reflects the situation in (1+2)-dimensional Minkowski spacetime (one temporal and two spatial dimensions) with the corresponding hyperboloids. The invariant hyperbolae displaced by spacelike intervals from the origin generate hyperboloids of one sheet, while the invariant hyperbolae displaced by timelike intervals from the origin generate hyperboloids of two sheets.
The (1+2)-dimensional boundary between space- and timelike hyperboloids, established by the events forming a zero spacetime interval to the origin, is made up by degenerating the hyperboloids to the light cone. In (1+1)-dimensions the hyperbolae degenerate to the two grey 45°-lines depicted in Fig. 2-7a.
Time dilation and length contraction[edit]
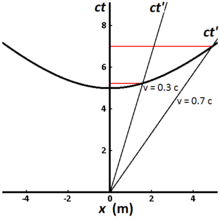
Fig. 2-8 illustrates the invariant hyperbola for all events that can be reached from the origin in a proper time of 5 meters (approximately 1.67×10−8 s). Different world lines represent clocks moving at different speeds. A clock that is stationary with respect to the observer has a world line that is vertical, and the elapsed time measured by the observer is the same as the proper time. For a clock traveling at 0.3 c, the elapsed time measured by the observer is 5.24 meters (1.75×10−8 s), while for a clock traveling at 0.7 c, the elapsed time measured by the observer is 7.00 meters (2.34×10−8 s).[3]: 220–221
This illustrates the phenomenon known as time dilation. Clocks that travel faster take longer (in the observer frame) to tick out the same amount of proper time, and they travel further along the x–axis within that proper time than they would have without time dilation.[3]: 220–221 The measurement of time dilation by two observers in different inertial reference frames is mutual. If observer O measures the clocks of observer O′ as running slower in his frame, observer O′ in turn will measure the clocks of observer O as running slower.

Length contraction, like time dilation, is a manifestation of the relativity of simultaneity. Measurement of length requires measurement of the spacetime interval between two events that are simultaneous in one's frame of reference. But events that are simultaneous in one frame of reference are, in general, not simultaneous in other frames of reference.
Fig. 2-9 illustrates the motions of a 1 m rod that is traveling at 0.5 c along the x axis. The edges of the blue band represent the world lines of the rod's two endpoints. The invariant hyperbola illustrates events separated from the origin by a spacelike interval of 1 m. The endpoints O and B measured when t′ = 0 are simultaneous events in the S′ frame. But to an observer in frame S, events O and B are not simultaneous. To measure length, the observer in frame S measures the endpoints of the rod as projected onto the x-axis along their world lines. The projection of the rod's world sheet onto the x axis yields the foreshortened length OC.[6]: 125
(not illustrated) Drawing a vertical line through A so that it intersects the x′ axis demonstrates that, even as OB is foreshortened from the point of view of observer O, OA is likewise foreshortened from the point of view of observer O′. In the same way that each observer measures the other's clocks as running slow, each observer measures the other's rulers as being contracted.
In regards to mutual length contraction, Fig. 2-9 illustrates that the primed and unprimed frames are mutually rotated by a hyperbolic angle (analogous to ordinary angles in Euclidean geometry).[note 8] Because of this rotation, the projection of a primed meter-stick onto the unprimed x-axis is foreshortened, while the projection of an unprimed meter-stick onto the primed x′-axis is likewise foreshortened.
Mutual time dilation and the twin paradox[edit]
Mutual time dilation[edit]
Mutual time dilation and length contraction tend to strike beginners as inherently self-contradictory concepts. If an observer in frame S measures a clock, at rest in frame S', as running slower than his', while S' is moving at speed v in S, then the principle of relativity requires that an observer in frame S' likewise measures a clock in frame S, moving at speed −v in S', as running slower than hers. How two clocks can run both slower than the other, is an important question that "goes to the heart of understanding special relativity."[3]: 198
This apparent contradiction stems from not correctly taking into account the different settings of the necessary, related measurements. These settings allow for a consistent explanation of the only apparent contradiction. It is not about the abstract ticking of two identical clocks, but about how to measure in one frame the temporal distance of two ticks of a moving clock. It turns out that in mutually observing the duration between ticks of clocks, each moving in the respective frame, different sets of clocks must be involved. In order to measure in frame S the tick duration of a moving clock W′ (at rest in S′), one uses two additional, synchronized clocks W1 and W2 at rest in two arbitrarily fixed points in S with the spatial distance d.
- Two events can be defined by the condition "two clocks are simultaneously at one place", i.e., when W′ passes each W1 and W2. For both events the two readings of the collocated clocks are recorded. The difference of the two readings of W1 and W2 is the temporal distance of the two events in S, and their spatial distance is d. The difference of the two readings of W′ is the temporal distance of the two events in S′. In S′ these events are only separated in time, they happen at the same place in S′. Because of the invariance of the spacetime interval spanned by these two events, and the nonzero spatial separation d in S, the temporal distance in S′ must be smaller than the one in S: the smaller temporal distance between the two events, resulting from the readings of the moving clock W′, belongs to the slower running clock W′.
Conversely, for judging in frame S′ the temporal distance of two events on a moving clock W (at rest in S), one needs two clocks at rest in S′.
- In this comparison the clock W is moving by with velocity −v. Recording again the four readings for the events, defined by "two clocks simultaneously at one place", results in the analogous temporal distances of the two events, now temporally and spatially separated in S′, and only temporally separated but collocated in S. To keep the spacetime interval invariant, the temporal distance in S must be smaller than in S′, because of the spatial separation of the events in S′: now clock W is observed to run slower.
The necessary recordings for the two judgements, with "one moving clock" and "two clocks at rest" in respectively S or S′, involves two different sets, each with three clocks. Since there are different sets of clocks involved in the measurements, there is no inherent necessity that the measurements be reciprocally "consistent" such that, if one observer measures the moving clock to be slow, the other observer measures the one's clock to be fast.[3]: 198–199
Fig. 2-10 illustrates the previous discussion of mutual time dilation with Minkowski diagrams. The upper picture reflects the measurements as seen from frame S "at rest" with unprimed, rectangular axes, and frame S′ "moving with v > 0", coordinatized by primed, oblique axes, slanted to the right; the lower picture shows frame S′ "at rest" with primed, rectangular coordinates, and frame S "moving with −v < 0", with unprimed, oblique axes, slanted to the left.
Each line drawn parallel to a spatial axis (x, x′) represents a line of simultaneity. All events on such a line have the same time value (ct, ct′). Likewise, each line drawn parallel to a temporal axis (ct, ct′) represents a line of equal spatial coordinate values (x, x′).
- One may designate in both pictures the origin O (= O′) as the event, where the respective "moving clock" is collocated with the "first clock at rest" in both comparisons. Obviously, for this event the readings on both clocks in both comparisons are zero. As a consequence, the worldlines of the moving clocks are the slanted to the right ct′-axis (upper pictures, clock W′) and the slanted to the left ct-axes (lower pictures, clock W). The worldlines of W1 and W′1 are the corresponding vertical time axes (ct in the upper pictures, and ct′ in the lower pictures).
- In the upper picture the place for W2 is taken to be Ax > 0, and thus the worldline (not shown in the pictures) of this clock intersects the worldline of the moving clock (the ct′-axis) in the event labelled A, where "two clocks are simultaneously at one place". In the lower picture the place for W′2 is taken to be Cx′ < 0, and so in this measurement the moving clock W passes W′2 in the event C.
- In the upper picture the ct-coordinate At of the event A (the reading of W2) is labeled B, thus giving the elapsed time between the two events, measured with W1 and W2, as OB. For a comparison, the length of the time interval OA, measured with W′, must be transformed to the scale of the ct-axis. This is done by the invariant hyperbola (see also Fig. 2-8) through A, connecting all events with the same spacetime interval from the origin as A. This yields the event C on the ct-axis, and obviously: OC < OB, the "moving" clock W′ runs slower.
To show the mutual time dilation immediately in the upper picture, the event D may be constructed as the event at x′ = 0 (the location of clock W′ in S′), that is simultaneous to C (OC has equal spacetime interval as OA) in S′. This shows that the time interval OD is longer than OA, showing that the "moving" clock runs slower.[6]: 124
In the lower picture the frame S is moving with velocity −v in the frame S′ at rest. The worldline of clock W is the ct-axis (slanted to the left), the worldline of W′1 is the vertical ct′-axis, and the worldline of W′2 is the vertical through event C, with ct′-coordinate D. The invariant hyperbola through event C scales the time interval OC to OA, which is shorter than OD; also, B is constructed (similar to D in the upper pictures) as simultaneous to A in S, at x = 0. The result OB > OC corresponds again to above.
The word "measure" is important. In classical physics an observer cannot affect an observed object, but the object's state of motion can affect the observer's observations of the object.
Twin paradox[edit]
Many introductions to special relativity illustrate the differences between Galilean relativity and special relativity by posing a series of "paradoxes". These paradoxes are, in fact, ill-posed problems, resulting from our unfamiliarity with velocities comparable to the speed of light. The remedy is to solve many problems in special relativity and to become familiar with its so-called counter-intuitive predictions. The geometrical approach to studying spacetime is considered one of the best methods for developing a modern intuition.[37]
The twin paradox is a thought experiment involving identical twins, one of whom makes a journey into space in a high-speed rocket, returning home to find that the twin who remained on Earth has aged more. This result appears puzzling because each twin observes the other twin as moving, and so at first glance, it would appear that each should find the other to have aged less. The twin paradox sidesteps the justification for mutual time dilation presented above by avoiding the requirement for a third clock.[3]: 207 Nevertheless, the twin paradox is not a true paradox because it is easily understood within the context of special relativity.
The impression that a paradox exists stems from a misunderstanding of what special relativity states. Special relativity does not declare all frames of reference to be equivalent, only inertial frames. The traveling twin's frame is not inertial during periods when she is accelerating. Furthermore, the difference between the twins is observationally detectable: the traveling twin needs to fire her rockets to be able to return home, while the stay-at-home twin does not.[38][note 9]
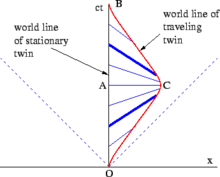
These distinctions should result in a difference in the twins' ages. The spacetime diagram of Fig. 2-11 presents the simple case of a twin going straight out along the x axis and immediately turning back. From the standpoint of the stay-at-home twin, there is nothing puzzling about the twin paradox at all. The proper time measured along the traveling twin's world line from O to C, plus the proper time measured from C to B, is less than the stay-at-home twin's proper time measured from O to A to B. More complex trajectories require integrating the proper time between the respective events along the curve (i.e. the path integral) to calculate the total amount of proper time experienced by the traveling twin.[38]
Complications arise if the twin paradox is analyzed from the traveling twin's point of view.
Weiss's nomenclature, designating the stay-at-home twin as Terence and the traveling twin as Stella, is hereafter used.[38]
Stella is not in an inertial frame. Given this fact, it is sometimes incorrectly stated that full resolution of the twin paradox requires general relativity:[38]
A pure SR analysis would be as follows: Analyzed in Stella's rest frame, she is motionless for the entire trip. When she fires her rockets for the turnaround, she experiences a pseudo force which resembles a gravitational force.[38] Figs. 2-6 and 2-11 illustrate the concept of lines (planes) of simultaneity: Lines parallel to the observer's x-axis (xy-plane) represent sets of events that are simultaneous in the observer frame. In Fig. 2-11, the blue lines connect events on Terence's world line which, from Stella's point of view, are simultaneous with events on her world line. (Terence, in turn, would observe a set of horizontal lines of simultaneity.) Throughout both the outbound and the inbound legs of Stella's journey, she measures Terence's clocks as running slower than her own. But during the turnaround (i.e. between the bold blue lines in the figure), a shift takes place in the angle of her lines of simultaneity, corresponding to a rapid skip-over of the events in Terence's world line that Stella considers to be simultaneous with her own. Therefore, at the end of her trip, Stella finds that Terence has aged more than she has.[38]
Although general relativity is not required to analyze the twin paradox, application of the Equivalence Principle of general relativity does provide some additional insight into the subject. Stella is not stationary in an inertial frame. Analyzed in Stella's rest frame, she is motionless for the entire trip. When she is coasting her rest frame is inertial, and Terence's clock will appear to run slow. But when she fires her rockets for the turnaround, her rest frame is an accelerated frame and she experiences a force which is pushing her as if she were in a gravitational field. Terence will appear to be high up in that field and because of gravitational time dilation, his clock will appear to run fast, so much so that the net result will be that Terence has aged more than Stella when they are back together.[38] The theoretical arguments predicting gravitational time dilation are not exclusive to general relativity. Any theory of gravity will predict gravitational time dilation if it respects the principle of equivalence, including Newton's theory.[3]: 16
Gravitation[edit]
This introductory section has focused on the spacetime of special relativity, since it is the easiest to describe. Minkowski spacetime is flat, takes no account of gravity, is uniform throughout, and serves as nothing more than a static background for the events that take place in it. The presence of gravity greatly complicates the description of spacetime. In general relativity, spacetime is no longer a static background, but actively interacts with the physical systems that it contains. Spacetime curves in the presence of matter, can propagate waves, bends light, and exhibits a host of other phenomena.[3]: 221 A few of these phenomena are described in the later sections of this article.
Basic mathematics of spacetime [edit]
Galilean transformations[edit]
A basic goal is to be able to compare measurements made by observers in relative motion. If there is an observer O in frame S who has measured the time and space coordinates of an event, assigning this event three Cartesian coordinates and the time as measured on his lattice of synchronized clocks (x, y, z, t) (see Fig. 1-1). A second observer O′ in a different frame S′ measures the same event in her coordinate system and her lattice of synchronized clocks (x′, y′, z′, t′). With inertial frames, neither observer is under acceleration, and a simple set of equations allows us to relate coordinates (x, y, z, t) to (x′, y′, z′, t′). Given that the two coordinate systems are in standard configuration, meaning that they are aligned with parallel (x, y, z) coordinates and that t = 0 when t′ = 0, the coordinate transformation is as follows:[39][40]
Fig. 3-1 illustrates that in Newton's theory, time is universal, not the velocity of light.[41]: 36–37 Consider the following thought experiment: The red arrow illustrates a train that is moving at 0.4 c with respect to the platform. Within the train, a passenger shoots a bullet with a speed of 0.4 c in the frame of the train. The blue arrow illustrates that a person standing on the train tracks measures the bullet as traveling at 0.8 c. This is in accordance with our naive expectations.
More generally, assuming that frame S′ is moving at velocity v with respect to frame S, then within frame S′, observer O′ measures an object moving with velocity u′. Velocity u with respect to frame S, since x = ut, x′ = x − vt, and t = t′, can be written as x′ = ut − vt = (u − v)t = (u − v)t′. This leads to u′ = x′/t′ and ultimately
- or
which is the common-sense Galilean law for the addition of velocities.
Relativistic composition of velocities[edit]

The composition of velocities is quite different in relativistic spacetime. To reduce the complexity of the equations slightly, we introduce a common shorthand for the ratio of the speed of an object relative to light,
Fig. 3-2a illustrates a red train that is moving forward at a speed given by v/c = β = s/a. From the primed frame of the train, a passenger shoots a bullet with a speed given by u′/c = β′ = n/m, where the distance is measured along a line parallel to the red x′ axis rather than parallel to the black x axis. What is the composite velocity u of the bullet relative to the platform, as represented by the blue arrow? Referring to Fig. 3-2b:
- From the platform, the composite speed of the bullet is given by u = c(s + r)/(a + b).
- The two yellow triangles are similar because they are right triangles that share a common angle α. In the large yellow triangle, the ratio s/a = v/c = β.
- The ratios of corresponding sides of the two yellow triangles are constant, so that r/a = b/s = n/m = β′. So b = u′s/c and r = u′a/c.
- Substitute the expressions for b and r into the expression for u in step 1 to yield Einstein's formula for the addition of velocities:[41]: 42–48
The relativistic formula for addition of velocities presented above exhibits several important features:
- If u′ and v are both very small compared with the speed of light, then the product vu′/c2 becomes vanishingly small, and the overall result becomes indistinguishable from the Galilean formula (Newton's formula) for the addition of velocities: u = u′ + v. The Galilean formula is a special case of the relativistic formula applicable to low velocities.
- If u′ is set equal to c, then the formula yields u = c regardless of the starting value of v. The velocity of light is the same for all observers regardless their motions relative to the emitting source.[41]: 49
Time dilation and length contraction revisited[edit]
This section needs additional citations for verification. (March 2024) |

It is straightforward to obtain quantitative expressions for time dilation and length contraction. Fig. 3-3 is a composite image containing individual frames taken from two previous animations, simplified and relabeled for the purposes of this section.
To reduce the complexity of the equations slightly, there are a variety of different shorthand notations for ct:
- and are common.
- One also sees very frequently the use of the convention
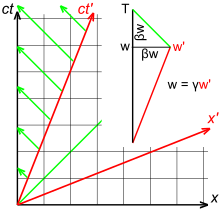
In Fig. 3-3a, segments OA and OK represent equal spacetime intervals. Time dilation is represented by the ratio OB/OK. The invariant hyperbola has the equation w = √x2 + k2 where k = OK, and the red line representing the world line of a particle in motion has the equation w = x/β = xc/v. A bit of algebraic manipulation yields
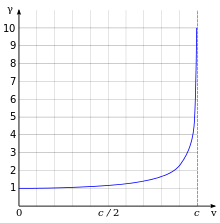
The expression involving the square root symbol appears very frequently in relativity, and one over the expression is called the Lorentz factor, denoted by the Greek letter gamma :[42]
If v is greater than or equal to c, the expression for becomes physically meaningless, implying that c is the maximum possible speed in nature. For any v greater than zero, the Lorentz factor will be greater than one, although the shape of the curve is such that for low speeds, the Lorentz factor is extremely close to one.
In Fig. 3-3b, segments OA and OK represent equal spacetime intervals. Length contraction is represented by the ratio OB/OK. The invariant hyperbola has the equation x = √w2 + k2, where k = OK, and the edges of the blue band representing the world lines of the endpoints of a rod in motion have slope 1/β = c/v. Event A has coordinates (x, w) = (γk, γβk). Since the tangent line through A and B has the equation w = (x − OB)/β, we have γβk = (γk − OB)/β and
Lorentz transformations[edit]
The Galilean transformations and their consequent commonsense law of addition of velocities work well in our ordinary low-speed world of planes, cars and balls. Beginning in the mid-1800s, however, sensitive scientific instrumentation began finding anomalies that did not fit well with the ordinary addition of velocities.
Lorentz transformations are used to transform the coordinates of an event from one frame to another in special relativity.
The Lorentz factor appears in the Lorentz transformations:
The inverse Lorentz transformations are:
When v ≪ c and x is small enough, the v2/c2 and vx/c2 terms approach zero, and the Lorentz transformations approximate to the Galilean transformations.
etc., most often really mean etc. Although for brevity the Lorentz transformation equations are written without deltas, x means Δx, etc. We are, in general, always concerned with the space and time differences between events.
Calling one set of transformations the normal Lorentz transformations and the other the inverse transformations is misleading, since there is no intrinsic difference between the frames. Different authors call one or the other set of transformations the "inverse" set. The forwards and inverse transformations are trivially related to each other, since the S frame can only be moving forwards or reverse with respect to S′. So inverting the equations simply entails switching the primed and unprimed variables and replacing v with −v.[43]: 71–79
Example: Terence and Stella are at an Earth-to-Mars space race. Terence is an official at the starting line, while Stella is a participant. At time t = t′ = 0, Stella's spaceship accelerates instantaneously to a speed of 0.5 c. The distance from Earth to Mars is 300 light-seconds (about 90.0×106 km). Terence observes Stella crossing the finish-line clock at t = 600.00 s. But Stella observes the time on her ship chronometer to be as she passes the finish line, and she calculates the distance between the starting and finish lines, as measured in her frame, to be 259.81 light-seconds (about 77.9×106 km). 1).
Deriving the Lorentz transformations[edit]
There have been many dozens of derivations of the Lorentz transformations since Einstein's original work in 1905, each with its particular focus. Although Einstein's derivation was based on the invariance of the speed of light, there are other physical principles that may serve as starting points. Ultimately, these alternative starting points can be considered different expressions of the underlying principle of locality, which states that the influence that one particle exerts on another can not be transmitted instantaneously.[44]
The derivation given here and illustrated in Fig. 3-5 is based on one presented by Bais[41]: 64–66 and makes use of previous results from the Relativistic Composition of Velocities, Time Dilation, and Length Contraction sections. Event P has coordinates (w, x) in the black "rest system" and coordinates (w′, x′) in the red frame that is moving with velocity parameter β = v/c. To determine w′ and x′ in terms of w and x (or the other way around) it is easier at first to derive the inverse Lorentz transformation.
- There can be no such thing as length expansion/contraction in the transverse directions. y' must equal y and z′ must equal z, otherwise whether a fast moving 1 m ball could fit through a 1 m circular hole would depend on the observer. The first postulate of relativity states that all inertial frames are equivalent, and transverse expansion/contraction would violate this law.[43]: 27–28
- From the drawing, w = a + b and x = r + s
- From previous results using similar triangles, we know that s/a = b/r = v/c = β.
- Because of time dilation, a = γw′
- Substituting equation (4) into s/a = β yields s = γw′β.
- Length contraction and similar triangles give us r = γx′ and b = βr = βγx′
- Substituting the expressions for s, a, r and b into the equations in Step 2 immediately yield
The above equations are alternate expressions for the t and x equations of the inverse Lorentz transformation, as can be seen by substituting ct for w, ct′ for w′, and v/c for β. From the inverse transformation, the equations of the forwards transformation can be derived by solving for t′ and x′.
Linearity of the Lorentz transformations[edit]
The Lorentz transformations have a mathematical property called linearity, since x′ and t′ are obtained as linear combinations of x and t, with no higher powers involved. The linearity of the transformation reflects a fundamental property of spacetime that was tacitly assumed in the derivation, namely, that the properties of inertial frames of reference are independent of location and time. In the absence of gravity, spacetime looks the same everywhere.[41]: 67 All inertial observers will agree on what constitutes accelerating and non-accelerating motion.[43]: 72–73 Any one observer can use her own measurements of space and time, but there is nothing absolute about them. Another observer's conventions will do just as well.[3]: 190
A result of linearity is that if two Lorentz transformations are applied sequentially, the result is also a Lorentz transformation.
Example: Terence observes Stella speeding away from him at 0.500 c, and he can use the Lorentz transformations with β = 0.500 to relate Stella's measurements to his own. Stella, in her frame, observes Ursula traveling away from her at 0.250 c, and she can use the Lorentz transformations with β = 0.250 to relate Ursula's measurements with her own. Because of the linearity of the transformations and the relativistic composition of velocities, Terence can use the Lorentz transformations with β = 0.666 to relate Ursula's measurements with his own.
Doppler effect[edit]
The Doppler effect is the change in frequency or wavelength of a wave for a receiver and source in relative motion. For simplicity, we consider here two basic scenarios: (1) The motions of the source and/or receiver are exactly along the line connecting them (longitudinal Doppler effect), and (2) the motions are at right angles to the said line (transverse Doppler effect). We are ignoring scenarios where they move along intermediate angles.
Longitudinal Doppler effect[edit]
The classical Doppler analysis deals with waves that are propagating in a medium, such as sound waves or water ripples, and which are transmitted between sources and receivers that are moving towards or away from each other. The analysis of such waves depends on whether the source, the receiver, or both are moving relative to the medium. Given the scenario where the receiver is stationary with respect to the medium, and the source is moving directly away from the receiver at a speed of vs for a velocity parameter of βs, the wavelength is increased, and the observed frequency f is given by
On the other hand, given the scenario where source is stationary, and the receiver is moving directly away from the source at a speed of vr for a velocity parameter of βr, the wavelength is not changed, but the transmission velocity of the waves relative to the receiver is decreased, and the observed frequency f is given by
Light, unlike sound or water ripples, does not propagate through a medium, and there is no distinction between a source moving away from the receiver or a receiver moving away from the source. Fig. 3-6 illustrates a relativistic spacetime diagram showing a source separating from the receiver with a velocity parameter so that the separation between source and receiver at time is . Because of time dilation, Since the slope of the green light ray is −1, Hence, the relativistic Doppler effect is given by[41]: 58–59
Transverse Doppler effect[edit]
Suppose that a source and a receiver, both approaching each other in uniform inertial motion along non-intersecting lines, are at their closest approach to each other. It would appear that the classical analysis predicts that the receiver detects no Doppler shift. Due to subtleties in the analysis, that expectation is not necessarily true. Nevertheless, when appropriately defined, transverse Doppler shift is a relativistic effect that has no classical analog. The subtleties are these:[45]: 541–543
- Fig. 3-7a. What is the frequency measurement when the receiver is geometrically at its closest approach to the source? This scenario is most easily analyzed from the frame S' of the source.[note 10]
- Fig. 3-7b. What is the frequency measurement when the receiver sees the source as being closest to it? This scenario is most easily analyzed from the frame S of the receiver.
Two other scenarios are commonly examined in discussions of transverse Doppler shift:
- Fig. 3-7c. If the receiver is moving in a circle around the source, what frequency does the receiver measure?
- Fig. 3-7d. If the source is moving in a circle around the receiver, what frequency does the receiver measure?
In scenario (a), the point of closest approach is frame-independent and represents the moment where there is no change in distance versus time (i.e. dr/dt = 0 where r is the distance between receiver and source) and hence no longitudinal Doppler shift. The source observes the receiver as being illuminated by light of frequency f′, but also observes the receiver as having a time-dilated clock. In frame S, the receiver is therefore illuminated by blueshifted light of frequency
In scenario (b) the illustration shows the receiver being illuminated by light from when the source was closest to the receiver, even though the source has moved on. Because the source's clocks are time dilated as measured in frame S, and since dr/dt was equal to zero at this point, the light from the source, emitted from this closest point, is redshifted with frequency
Scenarios (c) and (d) can be analyzed by simple time dilation arguments. In (c), the receiver observes light from the source as being blueshifted by a factor of , and in (d), the light is redshifted. The only seeming complication is that the orbiting objects are in accelerated motion. However, if an inertial observer looks at an accelerating clock, only the clock's instantaneous speed is important when computing time dilation. (The converse, however, is not true.)[45]: 541–543 Most reports of transverse Doppler shift refer to the effect as a redshift and analyze the effect in terms of scenarios (b) or (d).[note 11]
Energy and momentum[edit]
Extending momentum to four dimensions[edit]

In classical mechanics, the state of motion of a particle is characterized by its mass and its velocity. Linear momentum, the product of a particle's mass and velocity, is a vector quantity, possessing the same direction as the velocity: p = mv. It is a conserved quantity, meaning that if a closed system is not affected by external forces, its total linear momentum cannot change.
In relativistic mechanics, the momentum vector is extended to four dimensions. Added to the momentum vector is a time component that allows the spacetime momentum vector to transform like the spacetime position vector . In exploring the properties of the spacetime momentum, we start, in Fig. 3-8a, by examining what a particle looks like at rest. In the rest frame, the spatial component of the momentum is zero, i.e. p = 0, but the time component equals mc.
We can obtain the transformed components of this vector in the moving frame by using the Lorentz transformations, or we can read it directly from the figure because we know that and , since the red axes are rescaled by gamma. Fig. 3-8b illustrates the situation as it appears in the moving frame. It is apparent that the space and time components of the four-momentum go to infinity as the velocity of the moving frame approaches c.[41]: 84–87
We will use this information shortly to obtain an expression for the four-momentum.
Momentum of light[edit]
Light particles, or photons, travel at the speed of c, the constant that is conventionally known as the speed of light. This statement is not a tautology, since many modern formulations of relativity do not start with constant speed of light as a postulate. Photons therefore propagate along a lightlike world line and, in appropriate units, have equal space and time components for every observer.
A consequence of Maxwell's theory of electromagnetism is that light carries energy and momentum, and that their ratio is a constant: . Rearranging, , and since for photons, the space and time components are equal, E/c must therefore be equated with the time component of the spacetime momentum vector.
Photons travel at the speed of light, yet have finite momentum and energy. For this to be so, the mass term in γmc must be zero, meaning that photons are massless particles. Infinity times zero is an ill-defined quantity, but E/c is well-defined.
By this analysis, if the energy of a photon equals E in the rest frame, it equals in a moving frame. This result can be derived by inspection of Fig. 3-9 or by application of the Lorentz transformations, and is consistent with the analysis of Doppler effect given previously.[41]: 88
Mass–energy relationship[edit]
Consideration of the interrelationships between the various components of the relativistic momentum vector led Einstein to several famous conclusions.
- In the low speed limit as β = v/c approaches zero, γ approaches 1, so the spatial component of the relativistic momentum approaches mv, the classical term for momentum. Following this perspective, γm can be interpreted as a relativistic generalization of m. Einstein proposed that the relativistic mass of an object increases with velocity according to the formula .
- Likewise, comparing the time component of the relativistic momentum with that of the photon, , so that Einstein arrived at the relationship . Simplified to the case of zero velocity, this is Einstein's famous equation relating energy and mass.
Another way of looking at the relationship between mass and energy is to consider a series expansion of γmc2 at low velocity:
The second term is just an expression for the kinetic energy of the particle. Mass indeed appears to be another form of energy.[41]: 90–92 [43]: 129–130, 180
The concept of relativistic mass that Einstein introduced in 1905, mrel, although amply validated every day in particle accelerators around the globe (or indeed in any instrumentation whose use depends on high velocity particles, such as electron microscopes,[46] old-fashioned color television sets, etc.), has nevertheless not proven to be a fruitful concept in physics in the sense that it is not a concept that has served as a basis for other theoretical development. Relativistic mass, for instance, plays no role in general relativity.
For this reason, as well as for pedagogical concerns, most physicists currently prefer a different terminology when referring to the relationship between mass and energy.[47] "Relativistic mass" is a deprecated term. The term "mass" by itself refers to the rest mass or invariant mass, and is equal to the invariant length of the relativistic momentum vector. Expressed as a formula,
This formula applies to all particles, massless as well as massive. For photons where mrest equals zero, it yields, .[41]: 90–92
Four-momentum[edit]
Because of the close relationship between mass and energy, the four-momentum (also called 4-momentum) is also called the energy–momentum 4-vector. Using an uppercase P to represent the four-momentum and a lowercase p to denote the spatial momentum, the four-momentum may be written as
- or alternatively,
- using the convention that [43]: 129–130, 180
Conservation laws[edit]
In physics, conservation laws state that certain particular measurable properties of an isolated physical system do not change as the system evolves over time. In 1915, Emmy Noether discovered that underlying each conservation law is a fundamental symmetry of nature.[48] The fact that physical processes don't care where in space they take place (space translation symmetry) yields conservation of momentum, the fact that such processes don't care when they take place (time translation symmetry) yields conservation of energy, and so on. In this section, we examine the Newtonian views of conservation of mass, momentum and energy from a relativistic perspective.
Total momentum[edit]
To understand how the Newtonian view of conservation of momentum needs to be modified in a relativistic context, we examine the problem of two colliding bodies limited to a single dimension.
In Newtonian mechanics, two extreme cases of this problem may be distinguished yielding mathematics of minimum complexity:
- (1) The two bodies rebound from each other in a completely elastic collision.
- (2) The two bodies stick together and continue moving as a single particle. This second case is the case of completely inelastic collision.
For both cases (1) and (2), momentum, mass, and total energy are conserved. However, kinetic energy is not conserved in cases of inelastic collision. A certain fraction of the initial kinetic energy is converted to heat.
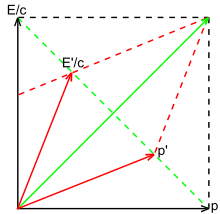
In case (2), two masses with momentums and collide to produce a single particle of conserved mass traveling at the center of mass velocity of the original system, . The total momentum is conserved.
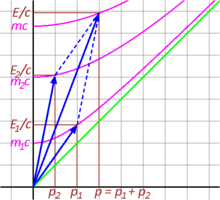
Fig. 3-10 illustrates the inelastic collision of two particles from a relativistic perspective. The time components and add up to total E/c of the resultant vector, meaning that energy is conserved. Likewise, the space components and add up to form p of the resultant vector. The four-momentum is, as expected, a conserved quantity. However, the invariant mass of the fused particle, given by the point where the invariant hyperbola of the total momentum intersects the energy axis, is not equal to the sum of the invariant masses of the individual particles that collided. Indeed, it is larger than the sum of the individual masses: .[41]: 94–97
Looking at the events of this scenario in reverse sequence, we see that non-conservation of mass is a common occurrence: when an unstable elementary particle spontaneously decays into two lighter particles, total energy is conserved, but the mass is not. Part of the mass is converted into kinetic energy.[43]: 134–138
Choice of reference frames[edit]
This section needs additional citations for verification. (March 2024) |
The freedom to choose any frame in which to perform an analysis allows us to pick one which may be particularly convenient. For analysis of momentum and energy problems, the most convenient frame is usually the "center-of-momentum frame" (also called the zero-momentum frame, or COM frame). This is the frame in which the space component of the system's total momentum is zero. Fig. 3-11 illustrates the breakup of a high speed particle into two daughter particles. In the lab frame, the daughter particles are preferentially emitted in a direction oriented along the original particle's trajectory. In the COM frame, however, the two daughter particles are emitted in opposite directions, although their masses and the magnitude of their velocities are generally not the same.
Energy and momentum conservation[edit]
In a Newtonian analysis of interacting particles, transformation between frames is simple because all that is necessary is to apply the Galilean transformation to all velocities. Since , the momentum . If the total momentum of an interacting system of particles is observed to be conserved in one frame, it will likewise be observed to be conserved in any other frame.[43]: 241–245
Conservation of momentum in the COM frame amounts to the requirement that p = 0 both before and after collision. In the Newtonian analysis, conservation of mass dictates that . In the simplified, one-dimensional scenarios that we have been considering, only one additional constraint is necessary before the outgoing momenta of the particles can be determined—an energy condition. In the one-dimensional case of a completely elastic collision with no loss of kinetic energy, the outgoing velocities of the rebounding particles in the COM frame will be precisely equal and opposite to their incoming velocities. In the case of a completely inelastic collision with total loss of kinetic energy, the outgoing velocities of the rebounding particles will be zero.[43]: 241–245
Newtonian momenta, calculated as , fail to behave properly under Lorentzian transformation. The linear transformation of velocities is replaced by the highly nonlinear so that a calculation demonstrating conservation of momentum in one frame will be invalid in other frames. Einstein was faced with either having to give up conservation of momentum, or to change the definition of momentum. This second option was what he chose.[41]: 104
The relativistic conservation law for energy and momentum replaces the three classical conservation laws for energy, momentum and mass. Mass is no longer conserved independently, because it has been subsumed into the total relativistic energy. This makes the relativistic conservation of energy a simpler concept than in nonrelativistic mechanics, because the total energy is conserved without any qualifications. Kinetic energy converted into heat or internal potential energy shows up as an increase in mass.[43]: 127
Fig. 3-12a illustrates the energy–momentum diagram for this decay reaction in the rest frame of the pion. Because of its negligible mass, a neutrino travels at very nearly the speed of light. The relativistic expression for its energy, like that of the photon, is which is also the value of the space component of its momentum. To conserve momentum, the muon has the same value of the space component of the neutrino's momentum, but in the opposite direction.
Algebraic analyses of the energetics of this decay reaction are available online,[49] so Fig. 3-12b presents instead a graphing calculator solution. The energy of the neutrino is 29.79 MeV, and the energy of the muon is 33.91 MeV − 29.79 MeV = 4.12 MeV. Most of the energy is carried off by the near-zero-mass neutrino.Beyond the basics[edit]
The topics in this section are of significantly greater technical difficulty than those in the preceding sections and are not essential for understanding Introduction to curved spacetime.
Rapidity[edit]
Lorentz transformations relate coordinates of events in one reference frame to those of another frame. Relativistic composition of velocities is used to add two velocities together. The formulas to perform the latter computations are nonlinear, making them more complex than the corresponding Galilean formulas.
This nonlinearity is an artifact of our choice of parameters.[9]: 47–59 We have previously noted that in an x–ct spacetime diagram, the points at some constant spacetime interval from the origin form an invariant hyperbola. We have also noted that the coordinate systems of two spacetime reference frames in standard configuration are hyperbolically rotated with respect to each other.
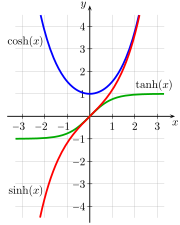
The natural functions for expressing these relationships are the hyperbolic analogs of the trigonometric functions. Fig. 4-1a shows a unit circle with sin(a) and cos(a), the only difference between this diagram and the familiar unit circle of elementary trigonometry being that a is interpreted, not as the angle between the ray and the x-axis, but as twice the area of the sector swept out by the ray from the x-axis. Numerically, the angle and 2 × area measures for the unit circle are identical. Fig. 4-1b shows a unit hyperbola with sinh(a) and cosh(a), where a is likewise interpreted as twice the tinted area.[50] Fig. 4-2 presents plots of the sinh, cosh, and tanh functions.
For the unit circle, the slope of the ray is given by
In the Cartesian plane, rotation of point (x, y) into point (x', y') by angle θ is given by
In a spacetime diagram, the velocity parameter is the analog of slope. The rapidity, φ, is defined by[43]: 96–99
where
The rapidity defined above is very useful in special relativity because many expressions take on a considerably simpler form when expressed in terms of it. For example, rapidity is simply additive in the collinear velocity-addition formula;[9]: 47–59
or in other words,
The Lorentz transformations take a simple form when expressed in terms of rapidity. The γ factor can be written as
Transformations describing relative motion with uniform velocity and without rotation of the space coordinate axes are called boosts.
Substituting γ and γβ into the transformations as previously presented and rewriting in matrix form, the Lorentz boost in the x-direction may be written as
and the inverse Lorentz boost in the x-direction may be written as
In other words, Lorentz boosts represent hyperbolic rotations in Minkowski spacetime.[43]: 96–99
The advantages of using hyperbolic functions are such that some textbooks such as the classic ones by Taylor and Wheeler introduce their use at a very early stage.[9][51][note 12]
4‑vectors[edit]
Four‑vectors have been mentioned above in context of the energy–momentum 4‑vector, but without any great emphasis. Indeed, none of the elementary derivations of special relativity require them. But once understood, 4‑vectors, and more generally tensors, greatly simplify the mathematics and conceptual understanding of special relativity. Working exclusively with such objects leads to formulas that are manifestly relativistically invariant, which is a considerable advantage in non-trivial contexts. For instance, demonstrating relativistic invariance of Maxwell's equations in their usual form is not trivial, while it is merely a routine calculation, really no more than an observation, using the field strength tensor formulation.[52]
On the other hand, general relativity, from the outset, relies heavily on 4‑vectors, and more generally tensors, representing physically relevant entities. Relating these via equations that do not rely on specific coordinates requires tensors, capable of connecting such 4‑vectors even within a curved spacetime, and not just within a flat one as in special relativity. The study of tensors is outside the scope of this article, which provides only a basic discussion of spacetime.
Definition of 4-vectors[edit]
A 4-tuple, is a "4-vector" if its component Ai transform between frames according to the Lorentz transformation.
If using coordinates, A is a 4–vector if it transforms (in the x-direction) according to
which comes from simply replacing ct with A0 and x with A1 in the earlier presentation of the Lorentz transformation.
As usual, when we write x, t, etc. we generally mean Δx, Δt etc.
The last three components of a 4–vector must be a standard vector in three-dimensional space. Therefore, a 4–vector must transform like under Lorentz transformations as well as rotations.[37]: 36–59
Properties of 4-vectors[edit]
- Closure under linear combination: If A and B are 4-vectors, then is also a 4-vector.
- Inner-product invariance: If A and B are 4-vectors, then their inner product (scalar product) is invariant, i.e. their inner product is independent of the frame in which it is calculated. Note how the calculation of inner product differs from the calculation of the inner product of a 3-vector. In the following, and are 3-vectors:
- In addition to being invariant under Lorentz transformation, the above inner product is also invariant under rotation in 3-space.
- Two vectors are said to be orthogonal if Unlike the case with 3-vectors, orthogonal 4-vectors are not necessarily at right angles with each other. The rule is that two 4-vectors are orthogonal if they are offset by equal and opposite angles from the 45° line which is the world line of a light ray. This implies that a lightlike 4-vector is orthogonal with itself.
- Invariance of the magnitude of a vector: The magnitude of a vector is the inner product of a 4-vector with itself, and is a frame-independent property. As with intervals, the magnitude may be positive, negative or zero, so that the vectors are referred to as timelike, spacelike or null (lightlike). Note that a null vector is not the same as a zero vector. A null vector is one for which while a zero vector is one whose components are all zero. Special cases illustrating the invariance of the norm include the invariant interval and the invariant length of the relativistic momentum vector [43]: 178–181 [37]: 36–59
Examples of 4-vectors[edit]
- Displacement 4-vector: Otherwise known as the spacetime separation, this is (Δt, Δx, Δy, Δz), or for infinitesimal separations, (dt, dx, dy, dz).
- Velocity 4-vector: This results when the displacement 4-vector is divided by , where is the proper time between the two events that yield dt, dx, dy, and dz.
- The 4-velocity is tangent to the world line of a particle, and has a length equal to one unit of time in the frame of the particle.
- An accelerated particle does not have an inertial frame in which it is always at rest. However, an inertial frame can always be found which is momentarily comoving with the particle. This frame, the momentarily comoving reference frame (MCRF), enables application of special relativity to the analysis of accelerated particles.
- Since photons move on null lines, for a photon, and a 4-velocity cannot be defined. There is no frame in which a photon is at rest, and no MCRF can be established along a photon's path.
- Energy–momentum 4-vector:
- As indicated before, there are varying treatments for the energy-momentum 4-vector so that one may also see it expressed as or The first component is the total energy (including mass) of the particle (or system of particles) in a given frame, while the remaining components are its spatial momentum. The energy-momentum 4-vector is a conserved quantity.
- Acceleration 4-vector: This results from taking the derivative of the velocity 4-vector with respect to
- Force 4-vector: This is the derivative of the momentum 4-vector with respect to
As expected, the final components of the above 4-vectors are all standard 3-vectors corresponding to spatial 3-momentum, 3-force etc.[43]: 178–181 [37]: 36–59
4-vectors and physical law[edit]
The first postulate of special relativity declares the equivalency of all inertial frames. A physical law holding in one frame must apply in all frames, since otherwise it would be possible to differentiate between frames. Newtonian momenta fail to behave properly under Lorentzian transformation, and Einstein preferred to change the definition of momentum to one involving 4-vectors rather than give up on conservation of momentum.
Physical laws must be based on constructs that are frame independent. This means that physical laws may take the form of equations connecting scalars, which are always frame independent. However, equations involving 4-vectors require the use of tensors with appropriate rank, which themselves can be thought of as being built up from 4-vectors.[43]: 186
Acceleration[edit]
It is a common misconception that special relativity is applicable only to inertial frames, and that it is unable to handle accelerating objects or accelerating reference frames. Actually, accelerating objects can generally be analyzed without needing to deal with accelerating frames at all. It is only when gravitation is significant that general relativity is required.[53]
Properly handling accelerating frames does require some care, however. The difference between special and general relativity is that (1) In special relativity, all velocities are relative, but acceleration is absolute. (2) In general relativity, all motion is relative, whether inertial, accelerating, or rotating. To accommodate this difference, general relativity uses curved spacetime.[53]
In this section, we analyze several scenarios involving accelerated reference frames.
Dewan–Beran–Bell spaceship paradox[edit]
The Dewan–Beran–Bell spaceship paradox (Bell's spaceship paradox) is a good example of a problem where intuitive reasoning unassisted by the geometric insight of the spacetime approach can lead to issues.

In Fig. 4-4, two identical spaceships float in space and are at rest relative to each other. They are connected by a string which is capable of only a limited amount of stretching before breaking. At a given instant in our frame, the observer frame, both spaceships accelerate in the same direction along the line between them with the same constant proper acceleration.[note 13] Will the string break?
When the paradox was new and relatively unknown, even professional physicists had difficulty working out the solution. Two lines of reasoning lead to opposite conclusions. Both arguments, which are presented below, are flawed even though one of them yields the correct answer.[43]: 106, 120–122
- To observers in the rest frame, the spaceships start a distance L apart and remain the same distance apart during acceleration. During acceleration, L is a length contracted distance of the distance L' = γL in the frame of the accelerating spaceships. After a sufficiently long time, γ will increase to a sufficiently large factor that the string must break.
- Let A and B be the rear and front spaceships. In the frame of the spaceships, each spaceship sees the other spaceship doing the same thing that it is doing. A says that B has the same acceleration that he has, and B sees that A matches her every move. So the spaceships stay the same distance apart, and the string does not break.[43]: 106, 120–122
The problem with the first argument is that there is no "frame of the spaceships." There cannot be, because the two spaceships measure a growing distance between the two. Because there is no common frame of the spaceships, the length of the string is ill-defined. Nevertheless, the conclusion is correct, and the argument is mostly right. The second argument, however, completely ignores the relativity of simultaneity.[43]: 106, 120–122
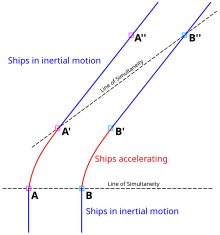
A spacetime diagram (Fig. 4-5) makes the correct solution to this paradox almost immediately evident. Two observers in Minkowski spacetime accelerate with constant magnitude acceleration for proper time (acceleration and elapsed time measured by the observers themselves, not some inertial observer). They are comoving and inertial before and after this phase. In Minkowski geometry, the length along the line of simultaneity turns out to be greater than the length along the line of simultaneity .
The length increase can be calculated with the help of the Lorentz transformation. If, as illustrated in Fig. 4-5, the acceleration is finished, the ships will remain at a constant offset in some frame If and are the ships' positions in the positions in frame are:[54]
The "paradox", as it were, comes from the way that Bell constructed his example. In the usual discussion of Lorentz contraction, the rest length is fixed and the moving length shortens as measured in frame . As shown in Fig. 4-5, Bell's example asserts the moving lengths and measured in frame to be fixed, thereby forcing the rest frame length in frame to increase.
Accelerated observer with horizon[edit]
Certain special relativity problem setups can lead to insight about phenomena normally associated with general relativity, such as event horizons. In the text accompanying Fig. 2-7, the magenta hyperbolae represented actual paths that are tracked by a constantly accelerating traveler in spacetime. During periods of positive acceleration, the traveler's velocity just approaches the speed of light, while, measured in our frame, the traveler's acceleration constantly decreases.
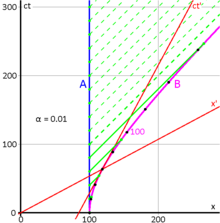
Fig. 4-6 details various features of the traveler's motions with more specificity. At any given moment, her space axis is formed by a line passing through the origin and her current position on the hyperbola, while her time axis is the tangent to the hyperbola at her position. The velocity parameter approaches a limit of one as increases. Likewise, approaches infinity.
The shape of the invariant hyperbola corresponds to a path of constant proper acceleration. This is demonstrable as follows:
- We remember that
- Since we conclude that
- From the relativistic force law,
- Substituting from step 2 and the expression for from step 3 yields which is a constant expression.[41]: 110–113
Fig. 4-6 illustrates a specific calculated scenario. Terence (A) and Stella (B) initially stand together 100 light hours from the origin. Stella lifts off at time 0, her spacecraft accelerating at 0.01 c per hour. Every twenty hours, Terence radios updates to Stella about the situation at home (solid green lines). Stella receives these regular transmissions, but the increasing distance (offset in part by time dilation) causes her to receive Terence's communications later and later as measured on her clock, and she never receives any communications from Terence after 100 hours on his clock (dashed green lines).[41]: 110–113
After 100 hours according to Terence's clock, Stella enters a dark region. She has traveled outside Terence's timelike future. On the other hand, Terence can continue to receive Stella's messages to him indefinitely. He just has to wait long enough. Spacetime has been divided into distinct regions separated by an apparent event horizon. So long as Stella continues to accelerate, she can never know what takes place behind this horizon.[41]: 110–113
Introduction to curved spacetime[edit]
Basic propositions[edit]
Newton's theories assumed that motion takes place against the backdrop of a rigid Euclidean reference frame that extends throughout all space and all time. Gravity is mediated by a mysterious force, acting instantaneously across a distance, whose actions are independent of the intervening space.[note 14] In contrast, Einstein denied that there is any background Euclidean reference frame that extends throughout space. Nor is there any such thing as a force of gravitation, only the structure of spacetime itself.[9]: 175–190
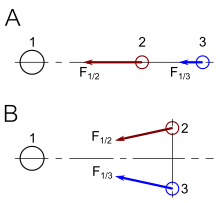
In spacetime terms, the path of a satellite orbiting the Earth is not dictated by the distant influences of the Earth, Moon and Sun. Instead, the satellite moves through space only in response to local conditions. Since spacetime is everywhere locally flat when considered on a sufficiently small scale, the satellite is always following a straight line in its local inertial frame. We say that the satellite always follows along the path of a geodesic. No evidence of gravitation can be discovered following alongside the motions of a single particle.[9]: 175–190
In any analysis of spacetime, evidence of gravitation requires that one observe the relative accelerations of two bodies or two separated particles. In Fig. 5-1, two separated particles, free-falling in the gravitational field of the Earth, exhibit tidal accelerations due to local inhomogeneities in the gravitational field such that each particle follows a different path through spacetime. The tidal accelerations that these particles exhibit with respect to each other do not require forces for their explanation. Rather, Einstein described them in terms of the geometry of spacetime, i.e. the curvature of spacetime. These tidal accelerations are strictly local. It is the cumulative total effect of many local manifestations of curvature that result in the appearance of a gravitational force acting at a long range from Earth.[9]: 175–190
Two central propositions underlie general relativity.
- The first crucial concept is coordinate independence: The laws of physics cannot depend on what coordinate system one uses. This is a major extension of the principle of relativity from the version used in special relativity, which states that the laws of physics must be the same for every observer moving in non-accelerated (inertial) reference frames. In general relativity, to use Einstein's own (translated) words, "the laws of physics must be of such a nature that they apply to systems of reference in any kind of motion."[55]: 113 This leads to an immediate issue: In accelerated frames, one feels forces that seemingly would enable one to assess one's state of acceleration in an absolute sense. Einstein resolved this problem through the principle of equivalence.[56]: 137–149

- The equivalence principle states that in any sufficiently small region of space, the effects of gravitation are the same as those from acceleration.
- In Fig. 5-2, person A is in a spaceship, far from any massive objects, that undergoes a uniform acceleration of g. Person B is in a box resting on Earth. Provided that the spaceship is sufficiently small so that tidal effects are non-measurable (given the sensitivity of current gravity measurement instrumentation, A and B presumably should be Lilliputians), there are no experiments that A and B can perform which will enable them to tell which setting they are in.[56]: 141–149
- An alternative expression of the equivalence principle is to note that in Newton's universal law of gravitation, F = GMmg/r2 = mgg and in Newton's second law, F = mia, there is no a priori reason why the gravitational mass mg should be equal to the inertial mass mi. The equivalence principle states that these two masses are identical.[56]: 141–149
To go from the elementary description above of curved spacetime to a complete description of gravitation requires tensor calculus and differential geometry, topics both requiring considerable study. Without these mathematical tools, it is possible to write about general relativity, but it is not possible to demonstrate any non-trivial derivations.
Curvature of time[edit]
In the discussion of special relativity, forces played no more than a background role. Special relativity assumes the ability to define inertial frames that fill all of spacetime, all of whose clocks run at the same rate as the clock at the origin. Is this really possible? In a nonuniform gravitational field, experiment dictates that the answer is no. Gravitational fields make it impossible to construct a global inertial frame. In small enough regions of spacetime, local inertial frames are still possible. General relativity involves the systematic stitching together of these local frames into a more general picture of spacetime.[37]: 118–126
Years before publication of the general theory in 1916, Einstein used the equivalence principle to predict the existence of gravitational redshift in the following thought experiment: (i) Assume that a tower of height h (Fig. 5-3) has been constructed. (ii) Drop a particle of rest mass m from the top of the tower. It falls freely with acceleration g, reaching the ground with velocity v = (2gh)1/2, so that its total energy E, as measured by an observer on the ground, is (iii) A mass-energy converter transforms the total energy of the particle into a single high energy photon, which it directs upward. (iv) At the top of the tower, an energy-mass converter transforms the energy of the photon E' back into a particle of rest mass m'.[37]: 118–126
It must be that m = m', since otherwise one would be able to construct a perpetual motion device. We therefore predict that E' = m, so that
A photon climbing in Earth's gravitational field loses energy and is redshifted. Early attempts to measure this redshift through astronomical observations were somewhat inconclusive, but definitive laboratory observations were performed by Pound & Rebka (1959) and later by Pound & Snider (1964).[57]
Light has an associated frequency, and this frequency may be used to drive the workings of a clock. The gravitational redshift leads to an important conclusion about time itself: Gravity makes time run slower. Suppose we build two identical clocks whose rates are controlled by some stable atomic transition. Place one clock on top of the tower, while the other clock remains on the ground. An experimenter on top of the tower observes that signals from the ground clock are lower in frequency than those of the clock next to her on the tower. Light going up the tower is just a wave, and it is impossible for wave crests to disappear on the way up. Exactly as many oscillations of light arrive at the top of the tower as were emitted at the bottom. The experimenter concludes that the ground clock is running slow, and can confirm this by bringing the tower clock down to compare side by side with the ground clock.[3]: 16–18 For a 1 km tower, the discrepancy would amount to about 9.4 nanoseconds per day, easily measurable with modern instrumentation.
Clocks in a gravitational field do not all run at the same rate. Experiments such as the Pound–Rebka experiment have firmly established curvature of the time component of spacetime. The Pound–Rebka experiment says nothing about curvature of the space component of spacetime. But the theoretical arguments predicting gravitational time dilation do not depend on the details of general relativity at all. Any theory of gravity will predict gravitational time dilation if it respects the principle of equivalence.[3]: 16 This includes Newtonian gravitation. A standard demonstration in general relativity is to show how, in the "Newtonian limit" (i.e. the particles are moving slowly, the gravitational field is weak, and the field is static), curvature of time alone is sufficient to derive Newton's law of gravity.[58]: 101–106
Newtonian gravitation is a theory of curved time. General relativity is a theory of curved time and curved space. Given G as the gravitational constant, M as the mass of a Newtonian star, and orbiting bodies of insignificant mass at distance r from the star, the spacetime interval for Newtonian gravitation is one for which only the time coefficient is variable:[3]: 229–232
Curvature of space[edit]
The coefficient in front of describes the curvature of time in Newtonian gravitation, and this curvature completely accounts for all Newtonian gravitational effects. As expected, this correction factor is directly proportional to and , and because of the in the denominator, the correction factor increases as one approaches the gravitating body, meaning that time is curved.
But general relativity is a theory of curved space and curved time, so if there are terms modifying the spatial components of the spacetime interval presented above, shouldn't their effects be seen on, say, planetary and satellite orbits due to curvature correction factors applied to the spatial terms?
The answer is that they are seen, but the effects are tiny. The reason is that planetary velocities are extremely small compared to the speed of light, so that for planets and satellites of the solar system, the term dwarfs the spatial terms.[3]: 234–238
Despite the minuteness of the spatial terms, the first indications that something was wrong with Newtonian gravitation were discovered over a century-and-a-half ago. In 1859, Urbain Le Verrier, in an analysis of available timed observations of transits of Mercury over the Sun's disk from 1697 to 1848, reported that known physics could not explain the orbit of Mercury, unless there possibly existed a planet or asteroid belt within the orbit of Mercury. The perihelion of Mercury's orbit exhibited an excess rate of precession over that which could be explained by the tugs of the other planets.[59] The ability to detect and accurately measure the minute value of this anomalous precession (only 43 arc seconds per tropical century) is testimony to the sophistication of 19th century astrometry.

As the famous astronomer who had earlier discovered the existence of Neptune "at the tip of his pen" by analyzing wobbles in the orbit of Uranus, Le Verrier's announcement triggered a two-decades long period of "Vulcan-mania", as professional and amateur astronomers alike hunted for the hypothetical new planet. This search included several false sightings of Vulcan. It was ultimately established that no such planet or asteroid belt existed.[60]
In 1916, Einstein was to show that this anomalous precession of Mercury is explained by the spatial terms in the curvature of spacetime. Curvature in the temporal term, being simply an expression of Newtonian gravitation, has no part in explaining this anomalous precession. The success of his calculation was a powerful indication to Einstein's peers that the general theory of relativity could be correct.
The most spectacular of Einstein's predictions was his calculation that the curvature terms in the spatial components of the spacetime interval could be measured in the bending of light around a massive body. Light has a slope of ±1 on a spacetime diagram. Its movement in space is equal to its movement in time. For the weak field expression of the invariant interval, Einstein calculated an exactly equal but opposite sign curvature in its spatial components.[3]: 234–238
In Newton's gravitation, the coefficient in front of predicts bending of light around a star. In general relativity, the coefficient in front of predicts a doubling of the total bending.[3]: 234–238
The story of the 1919 Eddington eclipse expedition and Einstein's rise to fame is well told elsewhere.[61]
Sources of spacetime curvature[edit]

In Newton's theory of gravitation, the only source of gravitational force is mass.
In contrast, general relativity identifies several sources of spacetime curvature in addition to mass. In the Einstein field equations, the sources of gravity are presented on the right-hand side in the stress–energy tensor.[62]
Fig. 5-5 classifies the various sources of gravity in the stress–energy tensor:
- (red): The total mass–energy density, including any contributions to the potential energy from forces between the particles, as well as kinetic energy from random thermal motions.
- and (orange): These are momentum density terms. Even if there is no bulk motion, energy may be transmitted by heat conduction, and the conducted energy will carry momentum.
- are the rates of flow of the i-component of momentum per unit area in the j-direction. Even if there is no bulk motion, random thermal motions of the particles will give rise to momentum flow, so the i = j terms (green) represent isotropic pressure, and the i ≠ j terms (blue) represent shear stresses.[62]
One important conclusion to be derived from the equations is that, colloquially speaking, gravity itself creates gravity.[note 15] Energy has mass. Even in Newtonian gravity, the gravitational field is associated with an energy, called the gravitational potential energy. In general relativity, the energy of the gravitational field feeds back into creation of the gravitational field. This makes the equations nonlinear and hard to solve in anything other than weak field cases.[3]: 240 Numerical relativity is a branch of general relativity using numerical methods to solve and analyze problems, often employing supercomputers to study black holes, gravitational waves, neutron stars and other phenomena in the strong field regime.
Energy-momentum[edit]
In special relativity, mass-energy is closely connected to momentum. Just as space and time are different aspects of a more comprehensive entity called spacetime, mass–energy and momentum are merely different aspects of a unified, four-dimensional quantity called four-momentum. In consequence, if mass–energy is a source of gravity, momentum must also be a source. The inclusion of momentum as a source of gravity leads to the prediction that moving or rotating masses can generate fields analogous to the magnetic fields generated by moving charges, a phenomenon known as gravitomagnetism.[63]

It is well known that the force of magnetism can be deduced by applying the rules of special relativity to moving charges. (An eloquent demonstration of this was presented by Feynman in volume II, chapter 13–6 of his Lectures on Physics, available online.)[64] Analogous logic can be used to demonstrate the origin of gravitomagnetism.[3]: 245–253
In Fig. 5-7a, two parallel, infinitely long streams of massive particles have equal and opposite velocities −v and +v relative to a test particle at rest and centered between the two. Because of the symmetry of the setup, the net force on the central particle is zero. Assume so that velocities are simply additive. Fig. 5-7b shows exactly the same setup, but in the frame of the upper stream. The test particle has a velocity of +v, and the bottom stream has a velocity of +2v. Since the physical situation has not changed, only the frame in which things are observed, the test particle should not be attracted towards either stream.[3]: 245–253
It is not at all clear that the forces exerted on the test particle are equal. (1) Since the bottom stream is moving faster than the top, each particle in the bottom stream has a larger mass energy than a particle in the top. (2) Because of Lorentz contraction, there are more particles per unit length in the bottom stream than in the top stream. (3) Another contribution to the active gravitational mass of the bottom stream comes from an additional pressure term which, at this point, we do not have sufficient background to discuss. All of these effects together would seemingly demand that the test particle be drawn towards the bottom stream.[3]: 245–253
The test particle is not drawn to the bottom stream because of a velocity-dependent force that serves to repel a particle that is moving in the same direction as the bottom stream. This velocity-dependent gravitational effect is gravitomagnetism.[3]: 245–253
Matter in motion through a gravitomagnetic field is hence subject to so-called frame-dragging effects analogous to electromagnetic induction. It has been proposed that such gravitomagnetic forces underlie the generation of the relativistic jets (Fig. 5-8) ejected by some rotating supermassive black holes.[65][66]
Pressure and stress[edit]
Quantities that are directly related to energy and momentum should be sources of gravity as well, namely internal pressure and stress. Taken together, mass-energy, momentum, pressure and stress all serve as sources of gravity: Collectively, they are what tells spacetime how to curve.
General relativity predicts that pressure acts as a gravitational source with exactly the same strength as mass–energy density. The inclusion of pressure as a source of gravity leads to dramatic differences between the predictions of general relativity versus those of Newtonian gravitation. For example, the pressure term sets a maximum limit to the mass of a neutron star. The more massive a neutron star, the more pressure is required to support its weight against gravity. The increased pressure, however, adds to the gravity acting on the star's mass. Above a certain mass determined by the Tolman–Oppenheimer–Volkoff limit, the process becomes runaway and the neutron star collapses to a black hole.[3]: 243, 280
The stress terms become highly significant when performing calculations such as hydrodynamic simulations of core-collapse supernovae.[67]
These predictions for the roles of pressure, momentum and stress as sources of spacetime curvature are elegant and play an important role in theory. In regards to pressure, the early universe was radiation dominated,[68] and it is highly unlikely that any of the relevant cosmological data (e.g. nucleosynthesis abundances, etc.) could be reproduced if pressure did not contribute to gravity, or if it did not have the same strength as a source of gravity as mass–energy. Likewise, the mathematical consistency of the Einstein field equations would be broken if the stress terms did not contribute as a source of gravity.
Experimental test of the sources of spacetime curvature[edit]
Definitions: Active, passive, and inertial mass[edit]
Bondi distinguishes between different possible types of mass: (1) active mass () is the mass which acts as the source of a gravitational field; (2)passive mass () is the mass which reacts to a gravitational field; (3) inertial mass () is the mass which reacts to acceleration.[69]
- is the same as gravitational mass () in the discussion of the equivalence principle.
In Newtonian theory,
- The third law of action and reaction dictates that and must be the same.
- On the other hand, whether and are equal is an empirical result.
In general relativity,
- The equality of and is dictated by the equivalence principle.
- There is no "action and reaction" principle dictating any necessary relationship between and .[69]
Pressure as a gravitational source[edit]
The classic experiment to measure the strength of a gravitational source (i.e. its active mass) was first conducted in 1797 by Henry Cavendish (Fig. 5-9a). Two small but dense balls are suspended on a fine wire, making a torsion balance. Bringing two large test masses close to the balls introduces a detectable torque. Given the dimensions of the apparatus and the measurable spring constant of the torsion wire, the gravitational constant G can be determined.
To study pressure effects by compressing the test masses is hopeless, because attainable laboratory pressures are insignificant in comparison with the mass-energy of a metal ball.
However, the repulsive electromagnetic pressures resulting from protons being tightly squeezed inside atomic nuclei are typically on the order of 1028 atm ≈ 1033 Pa ≈ 1033 kg·s−2m−1. This amounts to about 1% of the nuclear mass density of approximately 1018kg/m3 (after factoring in c2 ≈ 9×1016m2s−2).[70]
If pressure does not act as a gravitational source, then the ratio should be lower for nuclei with higher atomic number Z, in which the electrostatic pressures are higher. L. B. Kreuzer (1968) did a Cavendish experiment using a Teflon mass suspended in a mixture of the liquids trichloroethylene and dibromoethane having the same buoyant density as the Teflon (Fig. 5-9b). Fluorine has atomic number Z = 9, while bromine has Z = 35. Kreuzer found that repositioning the Teflon mass caused no differential deflection of the torsion bar, hence establishing active mass and passive mass to be equivalent to a precision of 5×10−5.[71]
Although Kreuzer originally considered this experiment merely to be a test of the ratio of active mass to passive mass, Clifford Will (1976) reinterpreted the experiment as a fundamental test of the coupling of sources to gravitational fields.[72]
In 1986, Bartlett and Van Buren noted that lunar laser ranging had detected a 2 km offset between the moon's center of figure and its center of mass. This indicates an asymmetry in the distribution of Fe (abundant in the Moon's core) and Al (abundant in its crust and mantle). If pressure did not contribute equally to spacetime curvature as does mass–energy, the moon would not be in the orbit predicted by classical mechanics. They used their measurements to tighten the limits on any discrepancies between active and passive mass to about 10−12.[73] With decades of additional lunar laser ranging data, Singh et al. (2023) reported improvement on these limits by a factor of about 100.[74]
Gravitomagnetism[edit]
The existence of gravitomagnetism was proven by Gravity Probe B (GP-B), a satellite-based mission which launched on 20 April 2004.[75] The spaceflight phase lasted until . The mission aim was to measure spacetime curvature near Earth, with particular emphasis on gravitomagnetism.
Initial results confirmed the relatively large geodetic effect (which is due to simple spacetime curvature, and is also known as de Sitter precession) to an accuracy of about 1%. The much smaller frame-dragging effect (which is due to gravitomagnetism, and is also known as Lense–Thirring precession) was difficult to measure because of unexpected charge effects causing variable drift in the gyroscopes. Nevertheless, by , the frame-dragging effect had been confirmed to within 15% of the expected result,[76] while the geodetic effect was confirmed to better than 0.5%.[77][78]
Subsequent measurements of frame dragging by laser-ranging observations of the LARES, LAGEOS-1 and LAGEOS-2 satellites has improved on the GP-B measurement, with results (as of 2016) demonstrating the effect to within 5% of its theoretical value,[79] although there has been some disagreement on the accuracy of this result.[80]
Another effort, the Gyroscopes in General Relativity (GINGER) experiment, seeks to use three 6 m ring lasers mounted at right angles to each other 1400 m below the Earth's surface to measure this effect.[81][82]
Technical topics[edit]
Is spacetime really curved?[edit]
In Poincaré's conventionalist views, the essential criteria according to which one should select a Euclidean versus non-Euclidean geometry would be economy and simplicity. A realist would say that Einstein discovered spacetime to be non-Euclidean. A conventionalist would say that Einstein merely found it more convenient to use non-Euclidean geometry. The conventionalist would maintain that Einstein's analysis said nothing about what the geometry of spacetime really is.[83]
Such being said,
- 1. Is it possible to represent general relativity in terms of flat spacetime?
- 2. Are there any situations where a flat spacetime interpretation of general relativity may be more convenient than the usual curved spacetime interpretation?
In response to the first question, a number of authors including Deser, Grishchuk, Rosen, Weinberg, etc. have provided various formulations of gravitation as a field in a flat manifold. Those theories are variously called "bimetric gravity", the "field-theoretical approach to general relativity", and so forth.[84][85][86][87] Kip Thorne has provided a popular review of these theories.[88]: 397–403
The flat spacetime paradigm posits that matter creates a gravitational field that causes rulers to shrink when they are turned from circumferential orientation to radial, and that causes the ticking rates of clocks to dilate. The flat spacetime paradigm is fully equivalent to the curved spacetime paradigm in that they both represent the same physical phenomena. However, their mathematical formulations are entirely different. Working physicists routinely switch between using curved and flat spacetime techniques depending on the requirements of the problem. The flat spacetime paradigm is convenient when performing approximate calculations in weak fields. Hence, flat spacetime techniques tend be used when solving gravitational wave problems, while curved spacetime techniques tend be used in the analysis of black holes.[88]: 397–403
Asymptotic symmetries[edit]
The spacetime symmetry group for Special Relativity is the Poincaré group, which is a ten-dimensional group of three Lorentz boosts, three rotations, and four spacetime translations. It is logical to ask what symmetries if any might apply in General Relativity. A tractable case might be to consider the symmetries of spacetime as seen by observers located far away from all sources of the gravitational field. The naive expectation for asymptotically flat spacetime symmetries might be simply to extend and reproduce the symmetries of flat spacetime of special relativity, viz., the Poincaré group.
In 1962 Hermann Bondi, M. G. van der Burg, A. W. Metzner[89] and Rainer K. Sachs[90] addressed this asymptotic symmetry problem in order to investigate the flow of energy at infinity due to propagating gravitational waves. Their first step was to decide on some physically sensible boundary conditions to place on the gravitational field at lightlike infinity to characterize what it means to say a metric is asymptotically flat, making no a priori assumptions about the nature of the asymptotic symmetry group—not even the assumption that such a group exists. Then after designing what they considered to be the most sensible boundary conditions, they investigated the nature of the resulting asymptotic symmetry transformations that leave invariant the form of the boundary conditions appropriate for asymptotically flat gravitational fields.[91]: 35
What they found was that the asymptotic symmetry transformations actually do form a group and the structure of this group does not depend on the particular gravitational field that happens to be present. This means that, as expected, one can separate the kinematics of spacetime from the dynamics of the gravitational field at least at spatial infinity. The puzzling surprise in 1962 was their discovery of a rich infinite-dimensional group (the so-called BMS group) as the asymptotic symmetry group, instead of the finite-dimensional Poincaré group, which is a subgroup of the BMS group. Not only are the Lorentz transformations asymptotic symmetry transformations, there are also additional transformations that are not Lorentz transformations but are asymptotic symmetry transformations. In fact, they found an additional infinity of transformation generators known as supertranslations. This implies the conclusion that General Relativity (GR) does not reduce to special relativity in the case of weak fields at long distances.[91]: 35
Riemannian geometry[edit]
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as smooth manifolds with a Riemannian metric (an inner product on the tangent space at each point that varies smoothly from point to point). This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions.
Riemannian geometry originated with the vision of Bernhard Riemann expressed in his inaugural lecture "Ueber die Hypothesen, welche der Geometrie zu Grunde liegen" ("On the Hypotheses on which Geometry is Based").[92] It is a very broad and abstract generalization of the differential geometry of surfaces in R3. Development of Riemannian geometry resulted in synthesis of diverse results concerning the geometry of surfaces and the behavior of geodesics on them, with techniques that can be applied to the study of differentiable manifolds of higher dimensions. It enabled the formulation of Einstein's general theory of relativity, made profound impact on group theory and representation theory, as well as analysis, and spurred the development of algebraic and differential topology.
Curved manifolds[edit]
For physical reasons, a spacetime continuum is mathematically defined as a four-dimensional, smooth, connected Lorentzian manifold . This means the smooth Lorentz metric has signature . The metric determines the geometry of spacetime, as well as determining the geodesics of particles and light beams. About each point (event) on this manifold, coordinate charts are used to represent observers in reference frames. Usually, Cartesian coordinates are used. Moreover, for simplicity's sake, units of measurement are usually chosen such that the speed of light is equal to 1.[93]
A reference frame (observer) can be identified with one of these coordinate charts; any such observer can describe any event . Another reference frame may be identified by a second coordinate chart about . Two observers (one in each reference frame) may describe the same event but obtain different descriptions.[93]
Usually, many overlapping coordinate charts are needed to cover a manifold. Given two coordinate charts, one containing (representing an observer) and another containing (representing another observer), the intersection of the charts represents the region of spacetime in which both observers can measure physical quantities and hence compare results. The relation between the two sets of measurements is given by a non-singular coordinate transformation on this intersection. The idea of coordinate charts as local observers who can perform measurements in their vicinity also makes good physical sense, as this is how one actually collects physical data—locally.[93]
For example, two observers, one of whom is on Earth, but the other one who is on a fast rocket to Jupiter, may observe a comet crashing into Jupiter (this is the event ). In general, they will disagree about the exact location and timing of this impact, i.e., they will have different 4-tuples (as they are using different coordinate systems). Although their kinematic descriptions will differ, dynamical (physical) laws, such as momentum conservation and the first law of thermodynamics, will still hold. In fact, relativity theory requires more than this in the sense that it stipulates these (and all other physical) laws must take the same form in all coordinate systems. This introduces tensors into relativity, by which all physical quantities are represented.
Geodesics are said to be timelike, null, or spacelike if the tangent vector to one point of the geodesic is of this nature. Paths of particles and light beams in spacetime are represented by timelike and null (lightlike) geodesics, respectively.[93]
Privileged character of 3+1 spacetime[edit]
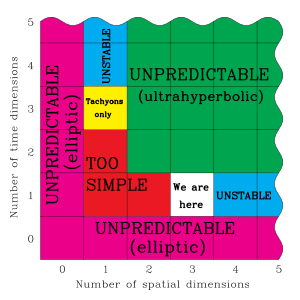
There are two kinds of dimensions: spatial (bidirectional) and temporal (unidirectional).[95] Let the number of spatial dimensions be N and the number of temporal dimensions be T. That N = 3 and T = 1, setting aside the compactified dimensions invoked by string theory and undetectable to date, can be explained by appealing to the physical consequences of letting N differ from 3 and T differ from 1. The argument is often of an anthropic character and possibly the first of its kind, albeit before the complete concept came into vogue.
The implicit notion that the dimensionality of the universe is special is first attributed to Gottfried Wilhelm Leibniz, who in the Discourse on Metaphysics suggested that the world is "the one which is at the same time the simplest in hypothesis and the richest in phenomena".[96] Immanuel Kant argued that 3-dimensional space was a consequence of the inverse square law of universal gravitation. While Kant's argument is historically important, John D. Barrow said that it "gets the punch-line back to front: it is the three-dimensionality of space that explains why we see inverse-square force laws in Nature, not vice-versa" (Barrow 2002:204).[note 16]
In 1920, Paul Ehrenfest showed that if there is only a single time dimension and more than three spatial dimensions, the orbit of a planet about its Sun cannot remain stable. The same is true of a star's orbit around the center of its galaxy.[97] Ehrenfest also showed that if there are an even number of spatial dimensions, then the different parts of a wave impulse will travel at different speeds. If there are spatial dimensions, where k is a positive whole number, then wave impulses become distorted. In 1922, Hermann Weyl claimed that Maxwell's theory of electromagnetism can be expressed in terms of an action only for a four-dimensional manifold.[98] Finally, Tangherlini showed in 1963 that when there are more than three spatial dimensions, electron orbitals around nuclei cannot be stable; electrons would either fall into the nucleus or disperse.[99]
Max Tegmark expands on the preceding argument in the following anthropic manner.[100] If T differs from 1, the behavior of physical systems could not be predicted reliably from knowledge of the relevant partial differential equations. In such a universe, intelligent life capable of manipulating technology could not emerge. Moreover, if T > 1, Tegmark maintains that protons and electrons would be unstable and could decay into particles having greater mass than themselves. (This is not a problem if the particles have a sufficiently low temperature.)[100] Lastly, if N < 3, gravitation of any kind becomes problematic, and the universe would probably be too simple to contain observers. For example, when N < 3, nerves cannot cross without intersecting.[100] Hence anthropic and other arguments rule out all cases except N = 3 and T = 1, which describes the world around us.
On the other hand, in view of creating black holes from an ideal monatomic gas under its self-gravity, Wei-Xiang Feng showed that (3+1)-dimensional spacetime is the marginal dimensionality. Moreover, it is the unique dimensionality that can afford a "stable" gas sphere with a "positive" cosmological constant. However, a self-gravitating gas cannot be stably bound if the mass sphere is larger than ~1021 solar masses, due to the small positivity of the cosmological constant observed.[101]
In 2019, James Scargill argued that complex life may be possible with two spatial dimensions. According to Scargill, a purely scalar theory of gravity may enable a local gravitational force, and 2D networks may be sufficient for complex neural networks.[102][103]See also[edit]
Notes[edit]
- ^ luminiferous from the Latin lumen, light, + ferens, carrying; aether from the Greek αἰθήρ (aithēr), pure air, clear sky
- ^ By stating that simultaneity is a matter of convention, Poincaré meant that to talk about time at all, one must have synchronized clocks, and the synchronization of clocks must be established by a specified, operational procedure (convention). This stance represented a fundamental philosophical break from Newton, who conceived of an absolute, true time that was independent of the workings of the inaccurate clocks of his day. This stance also represented a direct attack against the influential philosopher Henri Bergson, who argued that time, simultaneity, and duration were matters of intuitive understanding.[19]
- ^ The operational procedure adopted by Poincaré was essentially identical to what is known as Einstein synchronization, even though a variant of it was already a widely used procedure by telegraphers in the middle 19th century. Basically, to synchronize two clocks, one flashes a light signal from one to the other, and adjusts for the time that the flash takes to arrive.[19]
- ^ A hallmark of Einstein's career, in fact, was his use of visualized thought experiments (Gedanken–Experimente) as a fundamental tool for understanding physical issues. For special relativity, he employed moving trains and flashes of lightning for his most penetrating insights. For curved spacetime, he considered a painter falling off a roof, accelerating elevators, blind beetles crawling on curved surfaces and the like. In his great Solvay Debates with Bohr on the nature of reality (1927 and 1930), he devised multiple imaginary contraptions intended to show, at least in concept, means whereby the Heisenberg uncertainty principle might be evaded. Finally, in a profound contribution to the literature on quantum mechanics, Einstein considered two particles briefly interacting and then flying apart so that their states are correlated, anticipating the phenomenon known as quantum entanglement.[24]
- ^ In the original version of this lecture, Minkowski continued to use such obsolescent terms as the ether, but the posthumous publication in 1915 of this lecture in the Annals of Physics (Annalen der Physik) was edited by Sommerfeld to remove this term. Sommerfeld also edited the published form of this lecture to revise Minkowski's judgement of Einstein from being a mere clarifier of the principle of relativity, to being its chief expositor.[25]
- ^ (In the following, the group G∞ is the Galilean group and the group Gc the Lorentz group.) "With respect to this it is clear that the group Gc in the limit for c = ∞, i.e. as group G∞, exactly becomes the full group belonging to Newtonian Mechanics. In this state of affairs, and since Gc is mathematically more intelligible than G∞, a mathematician may, by a free play of imagination, hit upon the thought that natural phenomena actually possess an invariance, not for the group G∞, but rather for a group Gc, where c is definitely finite, and only exceedingly large using the ordinary measuring units."[27]
- ^ For instance, the Lorentz group is a subgroup of the conformal group in four dimensions.[28]: 41–42 The Lorentz group is isomorphic to the Laguerre group transforming planes into planes,[28]: 39–42 it is isomorphic to the Möbius group of the plane,[29]: 22 and is isomorphic to the group of isometries in hyperbolic space which is often expressed in terms of the hyperboloid model.[30]: 3.2.3
- ^ In a Cartesian plane, ordinary rotation leaves a circle unchanged. In spacetime, hyperbolic rotation preserves the hyperbolic metric.
- ^ Even with no (de)acceleration i.e. using one inertial frame O for constant, high-velocity outward journey and another inertial frame I for constant, high-velocity inward journey – the sum of the elapsed time in those frames (O and I) is shorter than the elapsed time in the stationary inertial frame S. Thus acceleration and deceleration is not the cause of shorter elapsed time during the outward and inward journey. Instead the use of two different constant, high-velocity inertial frames for outward and inward journey is really the cause of shorter elapsed time total. Granted, if the same twin has to travel outward and inward leg of the journey and safely switch from outward to inward leg of the journey, the acceleration and deceleration is required. If the travelling twin could ride the high-velocity outward inertial frame and instantaneously switch to high-velocity inward inertial frame the example would still work. The point is that real reason should be stated clearly. The asymmetry is because of the comparison of sum of elapsed times in two different inertial frames (O and I) to the elapsed time in a single inertial frame S.
- ^ The ease of analyzing a relativistic scenario often depends on the frame in which one chooses to perform the analysis. In this linked image, we present alternative views of the transverse Doppler shift scenario where source and receiver are at their closest approach to each other. (a) If we analyze the scenario in the frame of the receiver, we find that the analysis is more complicated than it should be. The apparent position of a celestial object is displaced from its true position (or geometric position) because of the object's motion during the time it takes its light to reach an observer. The source would be time-dilated relative to the receiver, but the redshift implied by this time dilation would be offset by a blueshift due to the longitudinal component of the relative motion between the receiver and the apparent position of the source. (b) It is much easier if, instead, we analyze the scenario from the frame of the source. An observer situated at the source knows, from the problem statement, that the receiver is at its closest point to him. That means that the receiver has no longitudinal component of motion to complicate the analysis. Since the receiver's clocks are time-dilated relative to the source, the light that the receiver receives is therefore blue-shifted by a factor of gamma.
- ^ Not all experiments characterize the effect in terms of a redshift. For example, the Kündig experiment measures transverse blueshift using a Mössbauer source setup at the center of a centrifuge rotor and an absorber at the rim.
- ^ Rapidity arises naturally as a coordinates on the pure boost generators inside the Lie algebra algebra of the Lorentz group. Likewise, rotation angles arise naturally as coordinates (modulo 2π) on the pure rotation generators in the Lie algebra. (Together they coordinatize the whole Lie algebra.) A notable difference is that the resulting rotations are periodic in the rotation angle, while the resulting boosts are not periodic in rapidity (but rather one-to-one). The similarity between boosts and rotations is formal resemblance.
- ^ In relativity theory, proper acceleration is the physical acceleration (i.e., measurable acceleration as by an accelerometer) experienced by an object. It is thus acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured.
- ^ Newton himself was acutely aware of the inherent difficulties with these assumptions, but as a practical matter, making these assumptions was the only way that he could make progress. In 1692, he wrote to his friend Richard Bentley: "That Gravity should be innate, inherent and essential to Matter, so that one body may act upon another at a distance thro' a Vacuum, without the Mediation of any thing else, by and through which their Action and Force may be conveyed from one to another, is to me so great an Absurdity that I believe no Man who has in philosophical Matters a competent Faculty of thinking can ever fall into it."
- ^ More precisely, the gravitational field couples to itself. In Newtonian gravity, the potential due to two point masses is simply the sum of the potentials of the two masses, but this does not apply to GR. This can be thought of as the result of the equivalence principle: If gravitation did not couple to itself, two particles bound by their mutual gravitational attraction would not have the same inertial mass (due to negative binding energy) as their gravitational mass.[58]: 112–113
- ^ This is because the law of gravitation (or any other inverse-square law) follows from the concept of flux and the proportional relationship of flux density and field strength. If N = 3, then 3-dimensional solid objects have surface areas proportional to the square of their size in any selected spatial dimension. In particular, a sphere of radius r has a surface area of 4πr2. More generally, in a space of N dimensions, the strength of the gravitational attraction between two bodies separated by a distance of r would be inversely proportional to rN−1.
Additional details[edit]
- ^ Different reporters viewing the scenarios presented in this figure interpret the scenarios differently depending on their knowledge of the situation. (i) A first reporter, at the center of mass of particles 2 and 3 but unaware of the large mass 1, concludes that a force of repulsion exists between the particles in scenario A while a force of attraction exists between the particles in scenario B. (ii) A second reporter, aware of the large mass 1, smiles at the first reporter's naiveté. This second reporter knows that in reality, the apparent forces between particles 2 and 3 really represent tidal effects resulting from their differential attraction by mass 1. (iii) A third reporter, trained in general relativity, knows that there are, in fact, no forces at all acting between the three objects. Rather, all three objects move along geodesics in spacetime.
References[edit]
- ^ Rynasiewicz, Robert (12 August 2004). "Newton's Views on Space, Time, and Motion". Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Archived from the original on 11 December 2015. Retrieved 24 March 2017.
- ^ Davis, Philip J. (2006). Mathematics & Common Sense: A Case of Creative Tension. Wellesley, Massachusetts: A.K. Peters. p. 86. ISBN 978-1-4398-6432-6.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z Schutz, Bernard (2004). Gravity from the Ground Up: An Introductory Guide to Gravity and General Relativity (Reprint ed.). Cambridge: Cambridge University Press. ISBN 0-521-45506-5. Archived from the original on 17 January 2023. Retrieved 24 May 2017.
- ^ Fock, V. (1966). The Theory of Space, Time and Gravitation (2nd ed.). New York: Pergamon Press Ltd. p. 33. ISBN 0-08-010061-9. Retrieved 14 October 2023.
- ^ Lawden, D. F. (1982). Introduction to Tensor Calculus, Relativity and Cosmology (3rd ed.). Mineola, New York: Dover Publications. p. 7. ISBN 978-0-486-42540-5.
- ^ a b c d e Collier, Peter (2017). A Most Incomprehensible Thing: Notes Towards a Very Gentle Introduction to the Mathematics of Relativity (3rd ed.). Incomprehensible Books. ISBN 978-0-9573894-6-5.
- ^ Rowland, Todd. "Manifold". Wolfram Mathworld. Wolfram Research. Archived from the original on 13 March 2017. Retrieved 24 March 2017.
- ^ a b French, A. P. (1968). Special Relativity. Boca Raton, Florida: CRC Press. pp. 35–60. ISBN 0-7487-6422-4.
- ^ a b c d e f g h i Taylor, Edwin F.; Wheeler, John Archibald (1992). Spacetime Physics: Introduction to Special Relativity (2nd ed.). San Francisco, California: Freeman. ISBN 0-7167-0336-X. Retrieved 14 April 2017.
- ^ Scherr, Rachel E.; Shaffer, Peter S.; Vokos, Stamatis (July 2001). "Student understanding of time in special relativity: Simultaneity and reference frames" (PDF). American Journal of Physics. 69 (S1). College Park, Maryland: American Association of Physics Teachers: S24–S35. arXiv:physics/0207109. Bibcode:2001AmJPh..69S..24S. doi:10.1119/1.1371254. S2CID 8146369. Archived (PDF) from the original on 28 September 2018. Retrieved 11 April 2017.
- ^ Hughes, Stefan (2013). Catchers of the Light: Catching Space: Origins, Lunar, Solar, Solar System and Deep Space. Paphos, Cyprus: ArtDeCiel Publishing. pp. 202–233. ISBN 978-1-4675-7992-6. Archived from the original on 17 January 2023. Retrieved 7 April 2017.
- ^ Williams, Matt (28 January 2022). "What is Einstein's Theory of Relativity?". Universe Today. Archived from the original on 3 August 2022. Retrieved 13 August 2022.
- ^ Stachel, John (2005). "Fresnel's (Dragging) Coefficient as a Challenge to 19th Century Optics of Moving Bodies." (PDF). In Kox, A. J.; Eisenstaedt, Jean (eds.). The Universe of General Relativity. Boston, Massachusetts: Birkhäuser. pp. 1–13. ISBN 0-8176-4380-X. Archived from the original (PDF) on 13 April 2017.
- ^ "George Francis FitzGerald". The Linda Hall Library. Archived from the original on 17 January 2023. Retrieved 13 August 2022.
- ^ "The Nobel Prize in Physics 1902". NobelPrize.org. Archived from the original on 23 June 2017. Retrieved 13 August 2022.
- ^ a b c Pais, Abraham (1982). 'Subtle is the Lord–': The Science and the Life of Albert Einstein (11th ed.). Oxford: Oxford University Press. ISBN 0-19-853907-X.
- ^ Darrigol, O. (2005), "The Genesis of the theory of relativity" (PDF), Séminaire Poincaré, 1: 1–22, Bibcode:2006eins.book....1D, doi:10.1007/3-7643-7436-5_1, ISBN 978-3-7643-7435-8, archived (PDF) from the original on 28 February 2008, retrieved 17 July 2017
- ^ Miller, Arthur I. (1998). Albert Einstein's Special Theory of Relativity. New York: Springer-Verlag. ISBN 0-387-94870-8.
- ^ a b c Galison, Peter (2003). Einstein's Clocks, Poincaré's Maps: Empires of Time. New York: W. W. Norton & Company, Inc. pp. 13–47. ISBN 0-393-02001-0.
- ^ Poincare, Henri (1906). "On the Dynamics of the Electron (Sur la dynamique de l'électron)". Rendiconti del Circolo Matematico di Palermo. 21: 129–176. Bibcode:1906RCMP...21..129P. doi:10.1007/bf03013466. hdl:2027/uiug.30112063899089. S2CID 120211823. Archived from the original on 11 July 2017. Retrieved 15 July 2017.
- ^ Zahar, Elie (1989) [1983], "Poincaré's Independent Discovery of the relativity principle", Einstein's Revolution: A Study in Heuristic, Chicago, Illinois: Open Court Publishing Company, ISBN 0-8126-9067-2
- ^ a b Walter, Scott A. (2007). "Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910". In Renn, Jürgen; Schemmel, Matthias (eds.). The Genesis of General Relativity, Volume 3. Berlin, Germany: Springer. pp. 193–252. Archived from the original on 15 July 2017. Retrieved 15 July 2017.
- ^ Einstein, Albert (1905). "On the Electrodynamics of Moving Bodies ( Zur Elektrodynamik bewegter Körper)". Annalen der Physik. 322 (10): 891–921. Bibcode:1905AnP...322..891E. doi:10.1002/andp.19053221004. Archived from the original on 6 November 2018. Retrieved 7 April 2018.
- ^ Isaacson, Walter (2007). Einstein: His Life and Universe. Simon & Schuster. pp. 26–27, 122–127, 145–146, 345–349, 448–460. ISBN 978-0-7432-6473-0.
- ^ a b Weinstein, Galina (2012). "Max Born, Albert Einstein and Hermann Minkowski's Space–Time Formalism of Special Relativity". arXiv:1210.6929 [physics.hist-ph].
- ^ Galison, Peter Louis (1979). "Minkowski's space–time: From visual thinking to the absolute world". Historical Studies in the Physical Sciences. 10: 85–121. doi:10.2307/27757388. JSTOR 27757388.
- ^ a b Minkowski, Hermann (1909). "Raum und Zeit" [Space and Time]. Jahresbericht der Deutschen Mathematiker-Vereinigung. B. G. Teubner: 1–14. Archived from the original on 28 July 2017. Retrieved 17 July 2017.
- ^ a b Cartan, É.; Fano, G. (1955) [1915]. "La théorie des groupes continus et la géométrie". Encyclopédie des Sciences Mathématiques Pures et Appliquées. 3 (1): 39–43. Archived from the original on 23 March 2018. Retrieved 6 April 2018. (Only pages 1–21 were published in 1915, the entire article including pp. 39–43 concerning the groups of Laguerre and Lorentz was posthumously published in 1955 in Cartan's collected papers, and was reprinted in the Encyclopédie in 1991.)
- ^ Kastrup, H. A. (2008). "On the advancements of conformal transformations and their associated symmetries in geometry and theoretical physics". Annalen der Physik. 520 (9–10): 631–690. arXiv:0808.2730. Bibcode:2008AnP...520..631K. doi:10.1002/andp.200810324. S2CID 12020510.
- ^ Ratcliffe, J. G. (1994). "Hyperbolic geometry". Foundations of Hyperbolic Manifolds. New York. pp. 56–104. ISBN 0-387-94348-X.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ a b c d e Kogut, John B. (2001). Introduction to Relativity. Massachusetts: Harcourt/Academic Press. ISBN 0-12-417561-9.
- ^ Ray d'Inverno; James Vickers (2022). Introducing Einstein's Relativity: A Deeper Understanding (illustrated ed.). Oxford University Press. pp. 26–28. ISBN 978-0-19-886202-4. Extract of page 27
- ^ Landau, L. D., and Lifshitz, E. M. (2013). The classical theory of fields (Vol. 2).
- ^ Carroll, Sean (2022). The Biggest Ideas in the Universe. New York: Penguin Random House LLC. pp. 155–156. ISBN 9780593186589.
- ^ Curiel, Erik; Bokulich, Peter. "Lightcones and Causal Structure". Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Archived from the original on 17 May 2019. Retrieved 26 March 2017.
- ^ a b Savitt, Steven. "Being and Becoming in Modern Physics. 3. The Special Theory of Relativity". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Archived from the original on 11 March 2017. Retrieved 26 March 2017.
- ^ a b c d e f Schutz, Bernard F. (1985). A first course in general relativity. Cambridge, UK: Cambridge University Press. p. 26. ISBN 0-521-27703-5.
- ^ a b c d e f g Weiss, Michael. "The Twin Paradox". The Physics and Relativity FAQ. Archived from the original on 27 April 2017. Retrieved 10 April 2017.
- ^ Mould, Richard A. (1994). Basic Relativity (1st ed.). Springer. p. 42. ISBN 978-0-387-95210-9. Retrieved 22 April 2017.
- ^ Lerner, Lawrence S. (1997). Physics for Scientists and Engineers, Volume 2 (1st ed.). Jones & Bartlett Pub. p. 1047. ISBN 978-0-7637-0460-5. Retrieved 22 April 2017.
- ^ a b c d e f g h i j k l m n o Bais, Sander (2007). Very Special Relativity: An Illustrated Guide. Cambridge, Massachusetts: Harvard University Press. ISBN 978-0-674-02611-7.
- ^ Forshaw, Jeffrey; Smith, Gavin (2014). Dynamics and Relativity. John Wiley & Sons. p. 118. ISBN 978-1-118-93329-9. Retrieved 24 April 2017.
- ^ a b c d e f g h i j k l m n o p q Morin, David (2017). Special Relativity for the Enthusiastic Beginner. CreateSpace Independent Publishing Platform. ISBN 978-1-5423-2351-2.
- ^ Landau, L. D.; Lifshitz, E. M. (2006). The Classical Theory of Fields, Course of Theoretical Physics, Volume 2 (4th ed.). Amsterdam: Elsevier. pp. 1–24. ISBN 978-0-7506-2768-9.
- ^ a b Morin, David (2008). Introduction to Classical Mechanics: With Problems and Solutions. Cambridge University Press. ISBN 978-0-521-87622-3.
- ^ Rose, H. H. (21 April 2008). "Optics of high-performance electron microscopes". Science and Technology of Advanced Materials. 9 (1): 014107. Bibcode:2008STAdM...9a4107R. doi:10.1088/0031-8949/9/1/014107. PMC 5099802. PMID 27877933.
- ^ Griffiths, David J. (2013). Revolutions in Twentieth-Century Physics. Cambridge: Cambridge University Press. p. 60. ISBN 978-1-107-60217-5. Retrieved 24 May 2017.
- ^ Byers, Nina (1998). "E. Noether's Discovery of the Deep Connection Between Symmetries and Conservation Laws". arXiv:physics/9807044.
- ^ Nave, R. "Energetics of Charged Pion Decay". Hyperphysics. Department of Physics and Astronomy, Georgia State University. Archived from the original on 21 May 2017. Retrieved 27 May 2017.
- ^ Thomas, George B.; Weir, Maurice D.; Hass, Joel; Giordano, Frank R. (2008). Thomas' Calculus: Early Transcendentals (Eleventh ed.). Boston: Pearson Education, Inc. p. 533. ISBN 978-0-321-49575-4.
- ^ Taylor, Edwin F.; Wheeler, John Archibald (1992). Spacetime Physics (2nd ed.). W. H. Freeman. ISBN 0-7167-2327-1.
- ^ E. J. Post (1962). Formal Structure of Electromagnetics: General Covariance and Electromagnetics. Dover Publications Inc. ISBN 978-0-486-65427-0.
- ^ a b Gibbs, Philip. "Can Special Relativity Handle Acceleration?". The Physics and Relativity FAQ. math.ucr.edu. Archived from the original on 7 June 2017. Retrieved 28 May 2017.
- ^ Franklin, Jerrold (2010). "Lorentz contraction, Bell's spaceships, and rigid body motion in special relativity". European Journal of Physics. 31 (2): 291–298. arXiv:0906.1919. Bibcode:2010EJPh...31..291F. doi:10.1088/0143-0807/31/2/006. S2CID 18059490.
- ^ Lorentz, H. A.; Einstein, A.; Minkowski, H.; Weyl, H. (1952). The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity. Dover Publications. ISBN 0-486-60081-5.
- ^ a b c Mook, Delo E.; Vargish, Thoma s (1987). Inside Relativity. Princeton, New Jersey: Princeton University Press. ISBN 0-691-08472-6.
- ^ Mester, John. "Experimental Tests of General Relativity" (PDF). Laboratoire Univers et Théories. Archived from the original (PDF) on 18 March 2017. Retrieved 9 June 2017.
- ^ a b Carroll, Sean M. (2 December 1997). "Lecture Notes on General Relativity". arXiv:gr-qc/9712019.
- ^ Le Verrier, Urbain (1859). "Lettre de M. Le Verrier à M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète". Comptes rendus hebdomadaires des séances de l'Académie des Sciences. 49: 379–383.
- ^ Worrall, Simon (4 November 2015). "The Hunt for Vulcan, the Planet That Wasn't There". National Geographic. Archived from the original on 24 May 2017.
- ^ Levine, Alaina G. (May 2016). "May 29, 1919: Eddington Observes Solar Eclipse to Test General Relativity". This Month in Physics History. APS News. American Physical Society. Archived from the original on 2 June 2017.
- ^ a b Hobson, M. P.; Efstathiou, G.; Lasenby, A. N. (2006). General Relativity. Cambridge: Cambridge University Press. pp. 176–179. ISBN 978-0-521-82951-9.
- ^ Thorne, Kip S. (1988). Fairbank, J. D.; Deaver, B. S. Jr.; Everitt, W. F.; Michelson, P. F. (eds.). Near zero: New Frontiers of Physics (PDF). W. H. Freeman and Company. pp. 573–586. S2CID 12925169. Archived from the original (PDF) on 28 July 2017.
- ^ Feynman, R. P.; Leighton, R. B.; Sands, M. (1964). The Feynman Lectures on Physics, vol. 2 (New Millenium ed.). Basic Books. pp. 13–6 to 13–11. ISBN 978-0-465-02416-2. Archived from the original on 17 January 2023. Retrieved 1 July 2017.
- ^ Williams, R. K. (1995). "Extracting X rays, Ύ rays, and relativistic e−–e+ pairs from supermassive Kerr black holes using the Penrose mechanism". Physical Review D. 51 (10): 5387–5427. Bibcode:1995PhRvD..51.5387W. doi:10.1103/PhysRevD.51.5387. PMID 10018300.
- ^ Williams, R. K. (2004). "Collimated escaping vortical polar e−–e+ jets intrinsically produced by rotating black holes and Penrose processes". The Astrophysical Journal. 611 (2): 952–963. arXiv:astro-ph/0404135. Bibcode:2004ApJ...611..952W. doi:10.1086/422304. S2CID 1350543.
- ^ Kuroda, Takami; Kotake, Kei; Takiwaki, Tomoya (2012). "Fully General Relativistic Simulations of Core-Collapse Supernovae with An Approximate Neutrino Transport". The Astrophysical Journal. 755 (1): 11. arXiv:1202.2487. Bibcode:2012ApJ...755...11K. doi:10.1088/0004-637X/755/1/11. S2CID 119179339.
- ^ Wollack, Edward J. (10 December 2010). "Cosmology: The Study of the Universe". Universe 101: Big Bang Theory. NASA. Archived from the original on 14 May 2011. Retrieved 15 April 2017.
- ^ a b Bondi, Hermann (1957). DeWitt, Cecile M.; Rickles, Dean (eds.). The Role of Gravitation in Physics: Report from the 1957 Chapel Hill Conference. Berlin, Germany: Max Planck Research Library. pp. 159–162. ISBN 978-3-86931-963-6. Archived from the original on 28 July 2017. Retrieved 1 July 2017.
- ^ Crowell, Benjamin (2000). General Relativity. Fullerton, CA: Light and Matter. pp. 241–258. Archived from the original on 18 June 2017. Retrieved 30 June 2017.
- ^ Kreuzer, L. B. (1968). "Experimental measurement of the equivalence of active and passive gravitational mass". Physical Review. 169 (5): 1007–1011. Bibcode:1968PhRv..169.1007K. doi:10.1103/PhysRev.169.1007.
- ^ Will, C. M. (1976). "Active mass in relativistic gravity-Theoretical interpretation of the Kreuzer experiment". The Astrophysical Journal. 204: 224–234. Bibcode:1976ApJ...204..224W. doi:10.1086/154164. Archived from the original on 28 September 2018. Retrieved 2 July 2017.
- ^ Bartlett, D. F.; Van Buren, Dave (1986). "Equivalence of active and passive gravitational mass using the moon". Physical Review Letters. 57 (1): 21–24. Bibcode:1986PhRvL..57...21B. doi:10.1103/PhysRevLett.57.21. PMID 10033347.
- ^ Singh, Vishwa Vijay; Müller, Jürgen; Biskupek, Liliane; Hackmann, Eva; Lämmerzahl, Claus (2023). "Equivalence of Active and Passive Gravitational Mass Tested with Lunar Laser Ranging". Physical Review Letters. 131 (2): 021401. arXiv:2212.09407. Bibcode:2023PhRvL.131b1401S. doi:10.1103/PhysRevLett.131.021401. PMID 37505941. Retrieved 7 March 2024.
- ^ "Gravity Probe B: FAQ". Archived from the original on 2 June 2018. Retrieved 2 July 2017.
- ^ Gugliotta, G. (16 February 2009). "Perseverance Is Paying Off for a Test of Relativity in Space". New York Times. Archived from the original on 3 September 2018. Retrieved 2 July 2017.
- ^ Everitt, C. W. F.; Parkinson, B. W. (2009). "Gravity Probe B Science Results—NASA Final Report" (PDF). Archived (PDF) from the original on 23 October 2012. Retrieved 2 July 2017.
- ^ Everitt; et al. (2011). "Gravity Probe B: Final Results of a Space Experiment to Test General Relativity". Physical Review Letters. 106 (22): 221101. arXiv:1105.3456. Bibcode:2011PhRvL.106v1101E. doi:10.1103/PhysRevLett.106.221101. PMID 21702590. S2CID 11878715.
- ^ Ciufolini, Ignazio; Paolozzi, Antonio Rolf Koenig; Pavlis, Erricos C.; Koenig, Rolf (2016). "A test of general relativity using the LARES and LAGEOS satellites and a GRACE Earth gravity model". European Physical Journal C. 76 (3): 120. arXiv:1603.09674. Bibcode:2016EPJC...76..120C. doi:10.1140/epjc/s10052-016-3961-8. PMC 4946852. PMID 27471430.
- ^ Iorio, L. (February 2017). "A comment on "A test of general relativity using the LARES and LAGEOS satellites and a GRACE Earth gravity model. Measurement of Earth's dragging of inertial frames," by I. Ciufolini et al". The European Physical Journal C. 77 (2): 73. arXiv:1701.06474. Bibcode:2017EPJC...77...73I. doi:10.1140/epjc/s10052-017-4607-1. S2CID 118945777.
- ^ Cartlidge, Edwin (20 January 2016). "Underground ring lasers will put general relativity to the test". physicsworld.com. Institute of Physics. Archived from the original on 12 July 2017. Retrieved 2 July 2017.
- ^ "Einstein right using the most sensitive Earth rotation sensors ever made". Phys.org. Science X network. Archived from the original on 10 May 2017. Retrieved 2 July 2017.
- ^ Murzi, Mauro. "Jules Henri Poincaré (1854–1912)". Internet Encyclopedia of Philosophy (ISSN 2161-0002). Archived from the original on 23 December 2020. Retrieved 9 April 2018.
- ^ Deser, S. (1970). "Self-Interaction and Gauge Invariance". General Relativity and Gravitation. 1 (18): 9–8. arXiv:gr-qc/0411023. Bibcode:1970GReGr...1....9D. doi:10.1007/BF00759198. S2CID 14295121.
- ^ Grishchuk, L. P.; Petrov, A. N.; Popova, A. D. (1984). "Exact Theory of the (Einstein) Gravitational Field in an Arbitrary Background Space–Time". Communications in Mathematical Physics. 94 (3): 379–396. Bibcode:1984CMaPh..94..379G. doi:10.1007/BF01224832. S2CID 120021772. Archived from the original on 25 February 2021. Retrieved 9 April 2018.
- ^ Rosen, N. (1940). "General Relativity and Flat Space I". Physical Review. 57 (2): 147–150. Bibcode:1940PhRv...57..147R. doi:10.1103/PhysRev.57.147.
- ^ Weinberg, S. (1964). "Derivation of Gauge Invariance and the Equivalence Principle from Lorentz Invariance of the S-Matrix". Physics Letters. 9 (4): 357–359. Bibcode:1964PhL.....9..357W. doi:10.1016/0031-9163(64)90396-8.
- ^ a b Thorne, Kip (1995). Black Holes & Time Warps: Einstein's Outrageous Legacy. W. W. Norton & Company. ISBN 978-0-393-31276-8.
- ^ Bondi, H.; Van der Burg, M. G. J.; Metzner, A. (1962). "Gravitational waves in general relativity: VII. Waves from axisymmetric isolated systems". Proceedings of the Royal Society of London A. A269 (1336): 21–52. Bibcode:1962RSPSA.269...21B. doi:10.1098/rspa.1962.0161. S2CID 120125096.
- ^ Sachs, Rainer K. (1962). "Asymptotic symmetries in gravitational theory". Physical Review. 128 (6): 2851–2864. Bibcode:1962PhRv..128.2851S. doi:10.1103/PhysRev.128.2851.
- ^ a b Strominger, Andrew (2017). "Lectures on the Infrared Structure of Gravity and Gauge Theory". arXiv:1703.05448 [hep-th].
...redacted transcript of a course given by the author at Harvard in spring semester 2016. It contains a pedagogical overview of recent developments connecting the subjects of soft theorems, the memory effect and asymptotic symmetries in four-dimensional QED, nonabelian gauge theory and gravity with applications to black holes. To be published Princeton University Press, 158 pages.
- ^ maths.tcd.ie
- ^ a b c d Bär, Christian; Fredenhagen, Klaus (2009). "Lorentzian Manifolds" (PDF). Quantum Field Theory on Curved Spacetimes: Concepts and Mathematical Foundations. Dordrecht: Springer. pp. 39–58. ISBN 978-3-642-02779-6. Archived from the original (PDF) on 13 April 2017. Retrieved 14 April 2017.
- ^ Tegmark, Max (1 April 1997). "On the dimensionality of spacetime". Classical and Quantum Gravity. 14 (4): L69–L75. arXiv:gr-qc/9702052. Bibcode:1997CQGra..14L..69T. doi:10.1088/0264-9381/14/4/002. ISSN 0264-9381. S2CID 250904081.
- ^ Skow, Bradford (2007). "What makes time different from space?" (PDF). Noûs. 41 (2): 227–252. CiteSeerX 10.1.1.404.7853. doi:10.1111/j.1468-0068.2007.00645.x. Archived from the original (PDF) on 24 August 2016. Retrieved 13 April 2018.
- ^ Leibniz, Gottfried (1880). "Discourse on metaphysics". Die philosophischen schriften von Gottfried Wilhelm Leibniz. Vol. 4. Weidmann. pp. 427–463. Retrieved 13 April 2018.
- ^ Ehrenfest, Paul (1920). "Welche Rolle spielt die Dreidimensionalität des Raumes in den Grundgesetzen der Physik?" [How do the fundamental laws of physics make manifest that space has 3 dimensions?]. Annalen der Physik. 61 (5): 440–446. Bibcode:1920AnP...366..440E. doi:10.1002/andp.19203660503.. Also see Ehrenfest, P. (1917) "In what way does it become manifest in the fundamental laws of physics that space has three dimensions?" Proceedings of the Amsterdam academy 20:200.
- ^ Weyl, H. (1922). Space, time, and matter. Dover reprint: 284.
- ^ Tangherlini, F. R. (1963). "Schwarzschild field in n dimensions and the dimensionality of space problem". Nuovo Cimento. 27 (3): 636–651. Bibcode:1963NCim...27..636T. doi:10.1007/BF02784569. S2CID 119683293.
- ^ a b c Tegmark, Max (April 1997). "On the dimensionality of spacetime" (PDF). Classical and Quantum Gravity. 14 (4): L69–L75. arXiv:gr-qc/9702052. Bibcode:1997CQGra..14L..69T. doi:10.1088/0264-9381/14/4/002. S2CID 15694111. Retrieved 16 December 2006.
- ^ Feng, W.X. (3 August 2022). "Gravothermal phase transition, black holes and space dimensionality". Physical Review D. 106 (4): L041501. arXiv:2207.14317. Bibcode:2022PhRvD.106d1501F. doi:10.1103/PhysRevD.106.L041501. S2CID 251196731.
- ^ Scargill, J. H. C. (26 February 2020). "Existence of life in 2 + 1 dimensions". Physical Review Research. 2 (1): 013217. arXiv:1906.05336. Bibcode:2020PhRvR...2a3217S. doi:10.1103/PhysRevResearch.2.013217. S2CID 211734117.
- ^ "Life could exist in a 2D universe (according to physics, anyway)". technologyreview.com. Retrieved 16 June 2021.
Further reading[edit]
- Barrow, John D.; Tipler, Frank J. (1986). The Anthropic Cosmological Principle (1st ed.). Oxford University Press. ISBN 978-0-19-282147-8. LCCN 87028148.
- George F. Ellis and Ruth M. Williams (1992) Flat and curved space–times. Oxford University Press. ISBN 0-19-851164-7
- Lorentz, H. A., Einstein, Albert, Minkowski, Hermann, and Weyl, Hermann (1952) The Principle of Relativity: A Collection of Original Memoirs. Dover.
- Lucas, John Randolph (1973) A Treatise on Time and Space. London: Methuen.
- Penrose, Roger (2004). The Road to Reality. Oxford: Oxford University Press. ISBN 0-679-45443-8. Chapters 17–18.
- Taylor, E. F.; Wheeler, John A. (1992). Spacetime Physics, Second Edition. Internet Archive: W. H. Freeman. ISBN 0-7167-2327-1.
- Arkani-Hamed, Nima (1 December 2017). The Doom of Spacetime: Why It Must Dissolve Into More Fundamental Structures (Speech). The 2,384th Meeting Of The Society. Washington, D.C. Retrieved 16 July 2022.
External links[edit]
 Media related to Spacetime at Wikimedia Commons
Media related to Spacetime at Wikimedia Commons- Albert Einstein on space–time 13th edition Encyclopædia Britannica Historical: Albert Einstein's 1926 article
- Encyclopedia of Space–time and gravitation Scholarpedia Expert articles
- Stanford Encyclopedia of Philosophy: "Space and Time: Inertial Frames" by Robert DiSalle.









































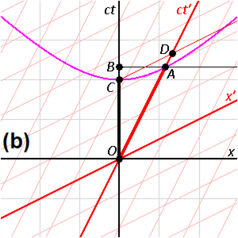






































































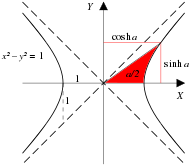


































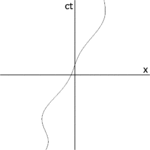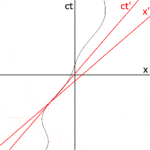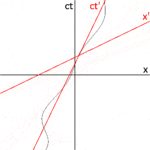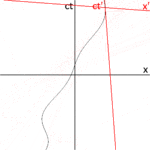









































![{\displaystyle -\,\left(1+{\frac {2GM}{c^{2}r}}\right)\left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e004b8eb220d5cc0f0e835a4f9a584ebfdc3ef02)

![{\displaystyle \left[(\Delta x)^{2}+(\Delta y)^{2}+(\Delta z)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b88b386b994cad15b04251eedd908b3828db4d66)

























