Metamaterial

A metamaterial (from the Greek word μετά meta, meaning "beyond" or "after", and the Latin word materia, meaning "matter" or "material") is any material engineered to have a property that is rarely observed in naturally occurring materials. They are made from assemblies of multiple elements fashioned from composite materials such as metals and plastics. These materials are usually arranged in repeating patterns, at scales that are smaller than the wavelengths of the phenomena they influence. Metamaterials derive their properties not from the properties of the base materials, but from their newly designed structures. Their precise shape, geometry, size, orientation and arrangement gives them their smart properties capable of manipulating electromagnetic waves: by blocking, absorbing, enhancing, or bending waves, to achieve benefits that go beyond what is possible with conventional materials.
Appropriately designed metamaterials can affect waves of electromagnetic radiation or sound in a manner not observed in bulk materials.[3][4][5] Those that exhibit a negative index of refraction for particular wavelengths have been the focus of a large amount of research.[6][7][8] These materials are known as negative-index metamaterials.
Potential applications of metamaterials are diverse and include optical filters, medical devices, remote aerospace applications, sensor detection and infrastructure monitoring, smart solar power management, Lasers,[9] crowd control, radomes, high-frequency battlefield communication and lenses for high-gain antennas, improving ultrasonic sensors, and even shielding structures from earthquakes.[10][11][12][13] Metamaterials offer the potential to create super-lenses.[14] Such a lens can allow imaging below the diffraction limit that is the minimum resolution d=λ/(2NA) that can be achieved by conventional lenses having a numerical aperture NA and with illumination wavelength λ. Sub-wavelength optical metamaterials, when integrated with optical recording media, can be used to achieve optical data density higher than limited by diffraction.[15] A form of 'invisibility' was demonstrated using gradient-index materials. Acoustic and seismic metamaterials are also research areas.[10][16]
Metamaterial research is interdisciplinary and involves such fields as electrical engineering, electromagnetics, classical optics, solid state physics, microwave and antenna engineering, optoelectronics, material sciences, nanoscience and semiconductor engineering.[4]
History[edit]
Explorations of artificial materials for manipulating electromagnetic waves began at the end of the 19th century. Some of the earliest structures that may be considered metamaterials were studied by Jagadish Chandra Bose, who in 1898 researched substances with chiral properties. Karl Ferdinand Lindman studied wave interaction with metallic helices as artificial chiral media in the early twentieth century.
In the late 1940s, Winston E. Kock from AT&T Bell Laboratories developed materials that had similar characteristics to metamaterials. In the 1950s and 1960s, artificial dielectrics were studied for lightweight microwave antennas. Microwave radar absorbers were researched in the 1980s and 1990s as applications for artificial chiral media.[4][17][18]
Negative-index materials were first described theoretically by Victor Veselago in 1967.[19] He proved that such materials could transmit light. He showed that the phase velocity could be made anti-parallel to the direction of Poynting vector. This is contrary to wave propagation in naturally occurring materials.[8]
In 1995, John M. Guerra fabricated a sub-wavelength transparent grating (later called a photonic metamaterial) having 50 nm lines and spaces, and then coupled it with a standard oil immersion microscope objective (the combination later called a super-lens) to resolve a grating in a silicon wafer also having 50 nm lines and spaces. This super-resolved image was achieved with illumination having a wavelength of 650 nm in air.[14]
In 2000, John Pendry was the first to identify a practical way to make a left-handed metamaterial, a material in which the right-hand rule is not followed.[19] Such a material allows an electromagnetic wave to convey energy (have a group velocity) against its phase velocity. Pendry's idea was that metallic wires aligned along the direction of a wave could provide negative permittivity (dielectric function ε < 0). Natural materials (such as ferroelectrics) display negative permittivity; the challenge was achieving negative permeability (µ < 0). In 1999 Pendry demonstrated that a split ring (C shape) with its axis placed along the direction of wave propagation could do so. In the same paper, he showed that a periodic array of wires and rings could give rise to a negative refractive index. Pendry also proposed a related negative-permeability design, the Swiss roll.
In 2000, David R. Smith et al. reported the experimental demonstration of functioning electromagnetic metamaterials by horizontally stacking, periodically, split-ring resonators and thin wire structures. A method was provided in 2002 to realize negative-index metamaterials using artificial lumped-element loaded transmission lines in microstrip technology. In 2003, complex (both real and imaginary parts of) negative refractive index[20] and imaging by flat lens[21] using left handed metamaterials were demonstrated. By 2007, experiments that involved negative refractive index had been conducted by many groups.[3][13] At microwave frequencies, the first, imperfect invisibility cloak was realized in 2006.[22][23][24][25][26]
From the standpoint of governing equations, contemporary researchers can classify the realm of metamaterials into three primary branches:[27] Electromagnetic/Optical wave metamaterials, other wave metamaterials, and diffusion metamaterials. These branches are characterized by their respective governing equations, which include Maxwell's equations (a wave equation describing transverse waves), other wave equations (for longitudinal and transverse waves), and diffusion equations (pertaining to diffusion processes).[28] Crafted to govern a range of diffusion activities, diffusion metamaterials prioritize diffusion length as their central metric. This crucial parameter experiences temporal fluctuations while remaining immune to frequency variations. In contrast, wave metamaterials, designed to adjust various wave propagation paths, consider the wavelength of incoming waves as their essential metric. This wavelength remains constant over time, though it adjusts with frequency alterations. Fundamentally, the key metrics for diffusion and wave metamaterials present a stark divergence, underscoring a distinct complementary relationship between them. For comprehensive information, please refer to Section I.B, "Evolution of metamaterial physics," in Ref.[27]
Electromagnetic metamaterials[edit]
| Articles about |
| Electromagnetism |
|---|
 |
An electromagnetic metamaterial affects electromagnetic waves that impinge on or interact with its structural features, which are smaller than the wavelength. To behave as a homogeneous material accurately described by an effective refractive index, its features must be much smaller than the wavelength.[citation needed]
The unusual properties of metamaterials arise from the resonant response of each constituent element rather that their spatial arrangement into a lattice. It allows considering the local effective material parameters (permittivity and permeability). The resonance effect related to the mutual arrangement of elements is responsible for Bragg scattering, which underlies the physics of photonic crystals, another class of electromagnetic materials. Unlike the local resonances, Bragg scattering and corresponding Bragg stop-band have a low-frequency limit determined by the lattice spacing. The subwavelength approximation ensures that the Bragg stop-bands with the strong spatial dispersion effects are at higher frequencies and can be neglected. The criterion for shifting the local resonance below the lower Bragg stop-band make it possible to build a photonic phase transition diagram in a parameter space, for example, size and permittivity of the constituent element. Such diagram displays the domain of structure parameters allowing the metamaterial properties observation in the electromagnetic material.[29]
For microwave radiation, the features are on the order of millimeters. Microwave frequency metamaterials are usually constructed as arrays of electrically conductive elements (such as loops of wire) that have suitable inductive and capacitive characteristics. Many microwave metamaterials use split-ring resonators.[5][6]
Photonic metamaterials are structured on the nanometer scale and manipulate light at optical frequencies. Photonic crystals and frequency-selective surfaces such as diffraction gratings, dielectric mirrors and optical coatings exhibit similarities to subwavelength structured metamaterials. However, these are usually considered distinct from metamaterials, as their function arises from diffraction or interference and thus cannot be approximated as a homogeneous material.[citation needed] However, material structures such as photonic crystals are effective in the visible light spectrum. The middle of the visible spectrum has a wavelength of approximately 560 nm (for sunlight). Photonic crystal structures are generally half this size or smaller, that is < 280 nm. [citation needed]
Plasmonic metamaterials utilize surface plasmons, which are packets of electrical charge that collectively oscillate at the surfaces of metals at optical frequencies.
Frequency selective surfaces (FSS) can exhibit subwavelength characteristics and are known variously as artificial magnetic conductors (AMC) or High Impedance Surfaces (HIS). FSS display inductive and capacitive characteristics that are directly related to their subwavelength structure.[30]
Electromagnetic metamaterials can be divided into different classes, as follows:[3][19][4][31]
Negative refractive index[edit]
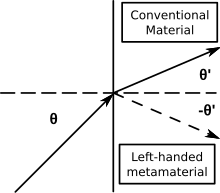
Negative-index metamaterials (NIM) are characterized by a negative index of refraction. Other terms for NIMs include "left-handed media", "media with a negative refractive index", and "backward-wave media".[3] NIMs where the negative index of refraction arises from simultaneously negative permittivity and negative permeability are also known as double negative metamaterials or double negative materials (DNG).[19]
Assuming a material well-approximated by a real permittivity and permeability, the relationship between permittivity , permeability and refractive index n is given by . All known non-metamaterial transparent materials (glass, water, ...) possess positive and . By convention the positive square root is used for n. However, some engineered metamaterials have and . Because the product is positive, n is real. Under such circumstances, it is necessary to take the negative square root for n. When both and are positive (negative), waves travel in the forward (backward) direction. Electromagnetic waves cannot propagate in materials with and of opposite sign as the refractive index becomes imaginary. Such materials are opaque for electromagnetic radiation and examples include plasmonic materials such as metals (gold, silver, ...).
The foregoing considerations are simplistic for actual materials, which must have complex-valued and . The real parts of both and do not have to be negative for a passive material to display negative refraction.[32][33] Indeed, a negative refractive index for circularly polarized waves can also arise from chirality.[34][35] Metamaterials with negative n have numerous interesting properties:[4][36]
- Snell's law (n1sinθ1 = n2sinθ2) still describes refraction, but as n2 is negative, incident and refracted rays are on the same side of the surface normal at an interface of positive and negative index materials.
- Cherenkov radiation points the other way.[further explanation needed]
- The time-averaged Poynting vector is antiparallel to phase velocity. However, for waves (energy) to propagate, a –µ must be paired with a –ε in order to satisfy the wave number dependence on the material parameters .
Negative index of refraction derives mathematically from the vector triplet E, H and k.[4]
For plane waves propagating in electromagnetic metamaterials, the electric field, magnetic field and wave vector follow a left-hand rule, the reverse of the behavior of conventional optical materials.
To date, only metamaterials exhibit a negative index of refraction.[3][36][37]
Single negative[edit]
Single negative (SNG) metamaterials have either negative relative permittivity (εr) or negative relative permeability (µr), but not both.[19] They act as metamaterials when combined with a different, complementary SNG, jointly acting as a DNG.
Epsilon negative media (ENG) display a negative εr while µr is positive.[3][36][19] Many plasmas exhibit this characteristic. For example, noble metals such as gold or silver are ENG in the infrared and visible spectrums.
Mu-negative media (MNG) display a positive εr and negative µr.[3][36][19] Gyrotropic or gyromagnetic materials exhibit this characteristic. A gyrotropic material is one that has been altered by the presence of a quasistatic magnetic field, enabling a magneto-optic effect.[citation needed] A magneto-optic effect is a phenomenon in which an electromagnetic wave propagates through such a medium. In such a material, left- and right-rotating elliptical polarizations can propagate at different speeds. When light is transmitted through a layer of magneto-optic material, the result is called the Faraday effect: the polarization plane can be rotated, forming a Faraday rotator. The results of such a reflection are known as the magneto-optic Kerr effect (not to be confused with the nonlinear Kerr effect). Two gyrotropic materials with reversed rotation directions of the two principal polarizations are called optical isomers.
Joining a slab of ENG material and slab of MNG material resulted in properties such as resonances, anomalous tunneling, transparency and zero reflection. Like negative-index materials, SNGs are innately dispersive, so their εr, µr and refraction index n, are a function of frequency.[36]
Hyperbolic[edit]
Hyperbolic metamaterials (HMMs) behave as a metal for certain polarization or direction of light propagation and behave as a dielectric for the other due to the negative and positive permittivity tensor components, giving extreme anisotropy. The material's dispersion relation in wavevector space forms a hyperboloid and therefore it is called a hyperbolic metamaterial. The extreme anisotropy of HMMs leads to directional propagation of light within and on the surface.[38] HMMs have showed various potential applications, such as sensing, reflection modulator,[39] imaging, steering of optical signals, enhanced plasmon resonance effects.[40]
Bandgap[edit]
Electromagnetic bandgap metamaterials (EBG or EBM) control light propagation. This is accomplished either with photonic crystals (PC) or left-handed materials (LHM). PCs can prohibit light propagation altogether. Both classes can allow light to propagate in specific, designed directions and both can be designed with bandgaps at desired frequencies.[41][42] The period size of EBGs is an appreciable fraction of the wavelength, creating constructive and destructive interference.
PC are distinguished from sub-wavelength structures, such as tunable metamaterials, because the PC derives its properties from its bandgap characteristics. PCs are sized to match the wavelength of light, versus other metamaterials that expose sub-wavelength structure. Furthermore, PCs function by diffracting light. In contrast, metamaterial does not use diffraction.[43]
PCs have periodic inclusions that inhibit wave propagation due to the inclusions' destructive interference from scattering. The photonic bandgap property of PCs makes them the electromagnetic analog of electronic semi-conductor crystals.[44]
EBGs have the goal of creating high quality, low loss, periodic, dielectric structures. An EBG affects photons in the same way semiconductor materials affect electrons. PCs are the perfect bandgap material, because they allow no light propagation.[45] Each unit of the prescribed periodic structure acts like one atom, albeit of a much larger size.[3][45]
EBGs are designed to prevent the propagation of an allocated bandwidth of frequencies, for certain arrival angles and polarizations. Various geometries and structures have been proposed to fabricate EBG's special properties. In practice it is impossible to build a flawless EBG device.[3][4]
EBGs have been manufactured for frequencies ranging from a few gigahertz (GHz) to a few terahertz (THz), radio, microwave and mid-infrared frequency regions. EBG application developments include a transmission line, woodpiles made of square dielectric bars and several different types of low gain antennas.[3][4]
Double positive medium[edit]
Double positive mediums (DPS) do occur in nature, such as naturally occurring dielectrics. Permittivity and magnetic permeability are both positive and wave propagation is in the forward direction. Artificial materials have been fabricated which combine DPS, ENG and MNG properties.[3][19]
Bi-isotropic and bianisotropic[edit]
Categorizing metamaterials into double or single negative, or double positive, normally assumes that the metamaterial has independent electric and magnetic responses described by ε and µ. However, in many cases, the electric field causes magnetic polarization, while the magnetic field induces electrical polarization, known as magnetoelectric coupling. Such media are denoted as bi-isotropic. Media that exhibit magnetoelectric coupling and that are anisotropic (which is the case for many metamaterial structures[46]), are referred to as bi-anisotropic.[47][48]
Four material parameters are intrinsic to magnetoelectric coupling of bi-isotropic media. They are the electric (E) and magnetic (H) field strengths, and electric (D) and magnetic (B) flux densities. These parameters are ε, µ, κ and χ or permittivity, permeability, strength of chirality, and the Tellegen parameter, respectively. In this type of media, material parameters do not vary with changes along a rotated coordinate system of measurements. In this sense they are invariant or scalar.[4]
The intrinsic magnetoelectric parameters, κ and χ, affect the phase of the wave. The effect of the chirality parameter is to split the refractive index. In isotropic media this results in wave propagation only if ε and µ have the same sign. In bi-isotropic media with χ assumed to be zero, and κ a non-zero value, different results appear. Either a backward wave or a forward wave can occur. Alternatively, two forward waves or two backward waves can occur, depending on the strength of the chirality parameter.
In the general case, the constitutive relations for bi-anisotropic materials read where and are the permittivity and the permeability tensors, respectively, whereas and are the two magneto-electric tensors. If the medium is reciprocal, permittivity and permeability are symmetric tensors, and , where is the chiral tensor describing chiral electromagnetic and reciprocal magneto-electric response. The chiral tensor can be expressed as , where is the trace of , I is the identity matrix, N is a symmetric trace-free tensor, and J is an antisymmetric tensor. Such decomposition allows us to classify the reciprocal bianisotropic response and we can identify the following three main classes: (i) chiral media (), (ii) pseudochiral media (), (iii) omega media ().
Chiral[edit]
Handedness of metamaterials is a potential source of confusion as the metamaterial literature includes two conflicting uses of the terms left- and right-handed. The first refers to one of the two circularly polarized waves that are the propagating modes in chiral media. The second relates to the triplet of electric field, magnetic field and Poynting vector that arise in negative refractive index media, which in most cases are not chiral.
Generally a chiral and/or bianisotropic electromagnetic response is a consequence of 3D geometrical chirality: 3D-chiral metamaterials are composed by embedding 3D-chiral structures in a host medium and they show chirality-related polarization effects such as optical activity and circular dichroism. The concept of 2D chirality also exists and a planar object is said to be chiral if it cannot be superposed onto its mirror image unless it is lifted from the plane. 2D-chiral metamaterials that are anisotropic and lossy have been observed to exhibit directionally asymmetric transmission (reflection, absorption) of circularly polarized waves due to circular conversion dichrosim.[49][50] On the other hand, bianisotropic response can arise from geometrical achiral structures possessing neither 2D nor 3D intrinsic chirality. Plum and colleagues investigated magneto-electric coupling due to extrinsic chirality, where the arrangement of a (achiral) structure together with the radiation wave vector is different from its mirror image, and observed large, tuneable linear optical activity,[51] nonlinear optical activity,[52] specular optical activity[53] and circular conversion dichroism.[54] Rizza et al.[55] suggested 1D chiral metamaterials where the effective chiral tensor is not vanishing if the system is geometrically one-dimensional chiral (the mirror image of the entire structure cannot be superposed onto it by using translations without rotations).
3D-chiral metamaterials are constructed from chiral materials or resonators in which the effective chirality parameter is non-zero. Wave propagation properties in such chiral metamaterials demonstrate that negative refraction can be realized in metamaterials with a strong chirality and positive and .[56] [57] This is because the refractive index has distinct values for left and right circularly polarized waves, given by
It can be seen that a negative index will occur for one polarization if > . In this case, it is not necessary that either or both and be negative for backward wave propagation.[4] A negative refractive index due to chirality was first observed simultaneously and independently by Plum et al.[34] and Zhang et al.[35] in 2009.
FSS based[edit]
Frequency selective surface-based metamaterials block signals in one waveband and pass those at another waveband. They have become an alternative to fixed frequency metamaterials. They allow for optional changes of frequencies in a single medium, rather than the restrictive limitations of a fixed frequency response.[58]
Other types[edit]
Elastic[edit]
These metamaterials use different parameters to achieve a negative index of refraction in materials that are not electromagnetic. Furthermore, "a new design for elastic metamaterials that can behave either as liquids or solids over a limited frequency range may enable new applications based on the control of acoustic, elastic and seismic waves."[59] They are also called mechanical metamaterials.[citation needed]
Acoustic[edit]
| Part of a series on |
| Continuum mechanics |
|---|
Acoustic metamaterials control, direct and manipulate sound in the form of sonic, infrasonic or ultrasonic waves in gases, liquids and solids. As with electromagnetic waves, sonic waves can exhibit negative refraction.[16]
Control of sound waves is mostly accomplished through the bulk modulus β, mass density ρ and chirality. The bulk modulus and density are analogs of permittivity and permeability in electromagnetic metamaterials. Related to this is the mechanics of sound wave propagation in a lattice structure. Also materials have mass and intrinsic degrees of stiffness. Together, these form a resonant system and the mechanical (sonic) resonance may be excited by appropriate sonic frequencies (for example audible pulses).
Structural[edit]
Structural metamaterials provide properties such as crushability and light weight. Using projection micro-stereolithography, microlattices can be created using forms much like trusses and girders. Materials four orders of magnitude stiffer than conventional aerogel, but with the same density have been created. Such materials can withstand a load of at least 160,000 times their own weight by over-constraining the materials.[60][61]
A ceramic nanotruss metamaterial can be flattened and revert to its original state.[62]
Thermal[edit]
Typically materials found in nature, when homogeneous, are thermally isotropic. That is to say, heat passes through them at roughly the same rate in all directions. However, thermal metamaterials are anisotropic usually due to their highly organized internal structure. Composite materials with highly aligned internal particles or structures, such as fibers, and carbon nanotubes (CNT), are examples of this.
Nonlinear[edit]
Metamaterials may be fabricated that include some form of nonlinear[disambiguation needed] media, whose properties change with the power of the incident wave. Nonlinear media are essential for nonlinear optics. Most optical materials have a relatively weak response, meaning that their properties change by only a small amount for large changes in the intensity of the electromagnetic field. The local electromagnetic fields of the inclusions in nonlinear metamaterials can be much larger than the average value of the field. Besides, remarkable nonlinear effects have been predicted and observed if the metamaterial effective dielectric permittivity is very small (epsilon-near-zero media).[63][64][65] In addition, exotic properties such as a negative refractive index, create opportunities to tailor the phase matching conditions that must be satisfied in any nonlinear optical structure.
Liquid[edit]
Metafluids offer programmable properties such as viscosity, compressibility, and optical. One approach employed 50-500 micron diameter air-filled elastomer spheres suspended in silicon oil. The spheres compress under pressure, and regain their shape when the pressure is relieved. Their properties differ across those two states. Unpressurized, they scatter light, making them opaque. Under pressure, they collapse into half-moon shapes, focusing light, and becoming transparent. The pressure response could allow them to act as a sensor or as a dynamic hydraulic fluid. Like cornstarch, it can act as either a Newtonian or a non-Newtonian fluid. Under pressure, it becomes non-Newtonian – meaning its viscosity changes in response to shear force.[66]
Hall metamaterials[edit]
In 2009, Marc Briane and Graeme Milton[67] proved mathematically that one can in principle invert the sign of a 3 materials based composite in 3D made out of only positive or negative sign Hall coefficient materials. Later in 2015 Muamer Kadic et al.[68] showed that a simple perforation of isotropic material can lead to its change of sign of the Hall coefficient. This theoretical claim was finally experimentally demonstrated by Christian Kern et al.[69]
In 2015, it was also demonstrated by Christian Kern et al. that an anisotropic perforation of a single material can lead to a yet more unusual effect namely the parallel Hall effect.[70] This means that the induced electric field inside a conducting media is no longer orthogonal to the current and the magnetic field but is actually parallel to the latest.
Meta-biomaterials[edit]
Meta-biomaterials have been purposefully crafted to engage with biological systems, amalgamating principles from both metamaterial science and biological areas. Engineered at the nanoscale, these materials adeptly manipulate electromagnetic, acoustic, or thermal properties to facilitate biological processes. Through meticulous adjustment of their structure and composition, meta-biomaterials hold promise in augmenting various biomedical technologies such as medical imaging,[71] drug delivery,[72] and tissue engineering.[73] This underscores the importance of comprehending biological systems through the interdisciplinary lens of materials science.
Frequency bands[edit]
Terahertz[edit]
Terahertz metamaterials interact at terahertz frequencies, usually defined as 0.1 to 10 THz. Terahertz radiation lies at the far end of the infrared band, just after the end of the microwave band. This corresponds to millimeter and submillimeter wavelengths between the 3 mm (EHF band) and 0.03 mm (long-wavelength edge of far-infrared light).
Photonic[edit]
Photonic metamaterial interact with optical frequencies (mid-infrared). The sub-wavelength period distinguishes them from photonic band gap structures.[74][75]
Tunable[edit]
Tunable metamaterials allow arbitrary adjustments to frequency changes in the refractive index. A tunable metamaterial expands beyond the bandwidth limitations in left-handed materials by constructing various types of metamaterials.
Plasmonic[edit]
Plasmonic metamaterials exploit surface plasmons, which are produced from the interaction of light with metal-dielectrics. Under specific conditions, the incident light couples with the surface plasmons to create self-sustaining, propagating electromagnetic waves or surface waves[76] known as surface plasmon polaritons. Bulk plasma oscillations make possible the effect of negative mass (density).[77][78]
Applications[edit]
Metamaterials are under consideration for many applications.[79] Metamaterial antennas are commercially available.
In 2007, one researcher stated that for metamaterial applications to be realized, energy loss must be reduced, materials must be extended into three-dimensional isotropic materials and production techniques must be industrialized.[80]
Antennas[edit]
Metamaterial antennas are a class of antennas that use metamaterials to improve performance.[13][19][81][82] Demonstrations showed that metamaterials could enhance an antenna's radiated power.[13][83] Materials that can attain negative permeability allow for properties such as small antenna size, high directivity and tunable frequency.[13][19]
Absorber[edit]
A metamaterial absorber manipulates the loss components of metamaterials' permittivity and magnetic permeability, to absorb large amounts of electromagnetic radiation.[84] This is a useful feature for photodetection[85][86] and solar photovoltaic applications.[87] Loss components are also relevant in applications of negative refractive index (photonic metamaterials, antenna systems) or transformation optics (metamaterial cloaking, celestial mechanics), but often are not used in these applications.
Superlens[edit]
A superlens is a two or three-dimensional device that uses metamaterials, usually with negative refraction properties, to achieve resolution beyond the diffraction limit (ideally, infinite resolution). Such a behaviour is enabled by the capability of double-negative materials to yield negative phase velocity. The diffraction limit is inherent in conventional optical devices or lenses.[88][89]
Cloaking devices[edit]
Metamaterials are a potential basis for a practical cloaking device. The proof of principle was demonstrated on October 19, 2006. No practical cloaks are publicly known to exist.[90][91][92][93][94][95]
Radar cross-section (RCS-)reducing metamaterials[edit]
Metamaterials have applications in stealth technology, which reduces RCS in any of various ways (e.g., absorption, diffusion, redirection). Conventionally, the RCS has been reduced either by radar-absorbent material (RAM) or by purpose shaping of the targets such that the scattered energy can be redirected away from the source. While RAMs have narrow frequency band functionality, purpose shaping limits the aerodynamic performance of the target. More recently, metamaterials or metasurfaces are synthesized that can redirect the scattered energy away from the source using either array theory[96][97][98][99] or generalized Snell's law.[100][101] This has led to aerodynamically favorable shapes for the targets with the reduced RCS.
Seismic protection[edit]
Seismic metamaterials counteract the adverse effects of seismic waves on man-made structures.[10][102][103]
Sound filtering[edit]
Metamaterials textured with nanoscale wrinkles could control sound or light signals, such as changing a material's color or improving ultrasound resolution. Uses include nondestructive material testing, medical diagnostics and sound suppression. The materials can be made through a high-precision, multi-layer deposition process. The thickness of each layer can be controlled within a fraction of a wavelength. The material is then compressed, creating precise wrinkles whose spacing can cause scattering of selected frequencies.[104][105]
Guided mode manipulations[edit]
Metamaterials can be integrated with optical waveguides to tailor guided electromagnetic waves (meta-waveguide).[106] Subwavelength structures like metamaterials can be integrated with for instance silicon waveguides to develop and polarization beam splitters[107] and optical couplers,[108] adding new degrees of freedom of controlling light propagation at nanoscale for integrated photonic devices.[109] Other applications such as integrated mode converters,[110] polarization (de)multiplexers,[111] structured light generation,[112] and on-chip bio-sensors[113] can be developed.[106]
Theoretical models[edit]
All materials are made of atoms, which are dipoles. These dipoles modify light velocity by a factor n (the refractive index). In a split ring resonator the ring and wire units act as atomic dipoles: the wire acts as a ferroelectric atom, while the ring acts as an inductor L, while the open section acts as a capacitor C. The ring as a whole acts as an LC circuit. When the electromagnetic field passes through the ring, an induced current is created. The generated field is perpendicular to the light's magnetic field. The magnetic resonance results in a negative permeability; the refraction index is negative as well. (The lens is not truly flat, since the structure's capacitance imposes a slope for the electric induction.)
Several (mathematical) material models frequency response in DNGs. One of these is the Lorentz model, which describes electron motion in terms of a driven-damped, harmonic oscillator. The Debye relaxation model applies when the acceleration component of the Lorentz mathematical model is small compared to the other components of the equation. The Drude model applies when the restoring force component is negligible and the coupling coefficient is generally the plasma frequency. Other component distinctions call for the use of one of these models, depending on its polarity or purpose.[3]
Three-dimensional composites of metal/non-metallic inclusions periodically/randomly embedded in a low permittivity matrix are usually modeled by analytical methods, including mixing formulas and scattering-matrix based methods. The particle is modeled by either an electric dipole parallel to the electric field or a pair of crossed electric and magnetic dipoles parallel to the electric and magnetic fields, respectively, of the applied wave. These dipoles are the leading terms in the multipole series. They are the only existing ones for a homogeneous sphere, whose polarizability can be easily obtained from the Mie scattering coefficients. In general, this procedure is known as the "point-dipole approximation", which is a good approximation for metamaterials consisting of composites of electrically small spheres. Merits of these methods include low calculation cost and mathematical simplicity.[114][115]
Three conceptions- negative-index medium, non-reflecting crystal and superlens are foundations of the metamaterial theory. Other first principles techniques for analyzing triply-periodic electromagnetic media may be found in Computing photonic band structure
Institutional networks[edit]
MURI[edit]
The Multidisciplinary University Research Initiative (MURI) encompasses dozens of Universities and a few government organizations. Participating universities include UC Berkeley, UC Los Angeles, UC San Diego, Massachusetts Institute of Technology, and Imperial College in London. The sponsors are Office of Naval Research and the Defense Advanced Research Project Agency.[116]
MURI supports research that intersects more than one traditional science and engineering discipline to accelerate both research and translation to applications. As of 2009, 69 academic institutions were expected to participate in 41 research efforts.[117]
Metamorphose[edit]
The Virtual Institute for Artificial Electromagnetic Materials and Metamaterials "Metamorphose VI AISBL" is an international association to promote artificial electromagnetic materials and metamaterials. It organizes scientific conferences, supports specialized journals, creates and manages research programs, provides training programs (including PhD and training programs for industrial partners); and technology transfer to European Industry.[118][119]
See also[edit]
- Metasurface
- Artificial dielectrics—macroscopic analogues of naturally occurring dielectrics that came into use with the radar microwave technologies developed between the 1940s and 1970s.
- METATOY (Metamaterial for rays)—composed of super-wavelength structures, such as small arrays of prisms and lenses and can operate over a broad band of frequencies
- Magnonics
- Metamaterials (journal)
- Metamaterials Handbook
- Metamaterials: Physics and Engineering Explorations
References[edit]
- ^ Shelby, R. A.; Smith D.R.; Shultz S.; Nemat-Nasser S.C. (2001). "Microwave transmission through a two-dimensional, isotropic, left-handed metamaterial" (PDF). Applied Physics Letters. 78 (4): 489. Bibcode:2001ApPhL..78..489S. doi:10.1063/1.1343489. Archived from the original (PDF) on June 18, 2010.
- ^ Smith, D. R.; Padilla, WJ; Vier, DC; Nemat-Nasser, SC; Schultz, S (2000). "Composite Medium with Simultaneously Negative Permeability and Permittivity". Physical Review Letters. 84 (18): 4184–87. Bibcode:2000PhRvL..84.4184S. doi:10.1103/PhysRevLett.84.4184. PMID 10990641.
- ^ a b c d e f g h i j k l Engheta, Nader; Richard W. Ziolkowski (June 2006). Metamaterials: Physics and Engineering Explorations. Wiley & Sons. pp. xv, 3–30, 37, 143–50, 215–34, 240–56. ISBN 978-0-471-76102-0.
- ^ a b c d e f g h i j Zouhdi, Saïd; Ari Sihvola; Alexey P. Vinogradov (December 2008). Metamaterials and Plasmonics: Fundamentals, Modelling, Applications. New York: Springer-Verlag. pp. 3–10, Chap. 3, 106. ISBN 978-1-4020-9406-4.
- ^ a b Smith, David R. (2006-06-10). "What are Electromagnetic Metamaterials?". Novel Electromagnetic Materials. The research group of D.R. Smith. Archived from the original on July 20, 2009. Retrieved 2009-08-19.
- ^ a b Shelby, R. A.; Smith, D. R.; Schultz, S. (2001). "Experimental Verification of a Negative Index of Refraction". Science. 292 (5514): 77–79. Bibcode:2001Sci...292...77S. CiteSeerX 10.1.1.119.1617. doi:10.1126/science.1058847. PMID 11292865. S2CID 9321456.
- ^ Pendry, John B. (2004). Negative Refraction (PDF). Vol. 45. Princeton University Press. pp. 191–202. Bibcode:2004ConPh..45..191P. doi:10.1080/00107510410001667434. ISBN 978-0-691-12347-9. S2CID 218544892. Archived from the original (PDF) on 2016-10-20. Retrieved 2009-08-26.
{{cite book}}:|journal=ignored (help) - ^ a b Veselago, V. G. (1968). "The electrodynamics of substances with simultaneously negative values of ε and μ". Physics-Uspekhi. 10 (4): 509–514. Bibcode:1968SvPhU..10..509V. doi:10.1070/PU1968v010n04ABEH003699.
- ^ Awad, Ehab (October 2021). "A novel metamaterial gain-waveguide nanolaser". Optics & Laser Technology. 142: 107202. Bibcode:2021OptLT.14207202A. doi:10.1016/j.optlastec.2021.107202.
- ^ a b c Brun, M.; S. Guenneau; and A.B. Movchan (2009-02-09). "Achieving control of in-plane elastic waves". Appl. Phys. Lett. 94 (61903): 061903. arXiv:0812.0912. Bibcode:2009ApPhL..94f1903B. doi:10.1063/1.3068491. S2CID 17568906.
- ^ Rainsford, Tamath J.; D. Abbott; Abbott, Derek (9 March 2005). Al-Sarawi, Said F (ed.). "T-ray sensing applications: review of global developments". Proc. SPIE. Smart Structures, Devices, and Systems II. 5649 Smart Structures, Devices, and Systems II (Poster session): 826–38. Bibcode:2005SPIE.5649..826R. doi:10.1117/12.607746. S2CID 14374107.
- ^ Cotton, Micheal G. (December 2003). "Applied Electromagnetics" (PDF). 2003 Technical Progress Report (NITA – ITS). Telecommunications Theory (3): 4–5. Archived from the original (PDF) on 2008-09-16. Retrieved 2009-09-14.
- ^ a b c d e Alici, Kamil Boratay; Özbay, Ekmel (2007). "Radiation properties of a split ring resonator and monopole composite". Physica Status Solidi B. 244 (4): 1192–96. Bibcode:2007PSSBR.244.1192A. doi:10.1002/pssb.200674505. hdl:11693/49278. S2CID 5348103.
- ^ a b Guerra, John M. (1995-06-26). "Super-resolution through illumination by diffraction-born evanescent waves". Applied Physics Letters. 66 (26): 3555–3557. Bibcode:1995ApPhL..66.3555G. doi:10.1063/1.113814. ISSN 0003-6951.
- ^ Guerra, John; Vezenov, Dmitri; Sullivan, Paul; Haimberger, Walter; Thulin, Lukas (2002-03-30). "Near-Field Optical Recording without Low-Flying Heads: Integral Near-Field Optical (INFO) Media". Japanese Journal of Applied Physics. 41 (Part 1, No. 3B): 1866–1875. Bibcode:2002JaJAP..41.1866G. doi:10.1143/jjap.41.1866. ISSN 0021-4922. S2CID 119544019.
- ^ a b Guenneau, S. B.; Movchan, A.; Pétursson, G.; Anantha Ramakrishna, S. (2007). "Acoustic metamaterials for sound focusing and confinement". New Journal of Physics. 9 (11): 399. Bibcode:2007NJPh....9..399G. doi:10.1088/1367-2630/9/11/399.
- ^ Zharov, Alexander A.; Zharova, Nina A.; Noskov, Roman E.; Shadrivov, Ilya V.; Kivshar, Yuri S. (2005). "Birefringent left-handed metamaterials and perfect lenses for vectorial fields". New Journal of Physics. 7 (1): 220. arXiv:physics/0412128. Bibcode:2005NJPh....7..220Z. doi:10.1088/1367-2630/7/1/220.
- ^ Bowers J. A.; Hyde R. A. et al. "Evanescent electromagnetic wave conversion lenses I, II, III" US Patent and Trademark Office, Grant US-9081202-B2, 14 juli 2015, U.S. patent 9,081,202
- ^ a b c d e f g h i j Slyusar, V.I. (October 6–9, 2009). Metamaterials on antenna solutions (PDF). 7th International Conference on Antenna Theory and Techniques ICATT’09. Lviv, Ukraine. pp. 19–24.
- ^ AIP News, Number 628 #1, March 13 Physics Today, May 2003, Press conference at APS March Meeting, Austin, Texas, March 4, 2003, New Scientist, vol 177, p. 24.
- ^ Parimi, P. V.; Lu, W. T.; Vodo, P; Sridhar, S (2003). "Photonic crystals: Imaging by flat lens using negative refraction". Nature. 426 (6965): 404. Bibcode:2003Natur.426..404P. doi:10.1038/426404a. PMID 14647372. S2CID 4411307.
- ^ Kock, W. E. (1946). "Metal-Lens Antennas". IRE Proc. 34 (11): 828–36. doi:10.1109/JRPROC.1946.232264. S2CID 51658054.
- ^ Kock, W.E. (1948). "Metallic Delay Lenses". Bell Syst. Tech. J. 27: 58–82. doi:10.1002/j.1538-7305.1948.tb01331.x.
- ^ Caloz, C.; Chang, C.-C.; Itoh, T. (2001). "Full-wave verification of the fundamental properties of left-handed materials in waveguide configurations" (PDF). J. Appl. Phys. 90 (11): 11. Bibcode:2001JAP....90.5483C. doi:10.1063/1.1408261. Archived from the original (PDF) on 2021-09-16. Retrieved 2009-05-17.
- ^ Eleftheriades, G.V.; Iyer A.K. & Kremer, P.C. (2002). "Planar Negative Refractive Index Media Using Periodically L-C Loaded Transmission Lines". IEEE Transactions on Microwave Theory and Techniques. 50 (12): 2702–12. Bibcode:2002ITMTT..50.2702E. doi:10.1109/TMTT.2002.805197.
- ^ Caloz, C.; Itoh, T. (2002). "Application of the transmission line theory of left-handed (LH) materials to the realization of a microstrip "LH line"". IEEE Antennas and Propagation Society International Symposium (IEEE Cat. No.02CH37313). Vol. 2. p. 412. doi:10.1109/APS.2002.1016111. ISBN 978-0-7803-7330-3. S2CID 108405740.
- ^ a b Yang, F.B.; Zhang, Z.R.; Xu, L.J.; Liu, Z.F.; Jin, P.; Zhuang, P.F.; Lei, M.; Liu, J.R.; Jiang, J.-H.; Ouyang, X.P.; Marchesoni, F.; Huang, J.P. (2024). "Controlling mass and energy diffusion with metamaterials". Rev. Mod. Phys. 96 (1): 015002. arXiv:2309.04711. doi:10.1103/RevModPhys.96.015002.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Yang, F.B.; Huang, J.P. (2024). Diffusionics: Diffusion Process Controlled by Diffusion Metamaterials. Singapore: Springer.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Rybin, M.V.; et al. (2015). "Phase diagram for the transition from photonic crystals to dielectric metamaterials". Nature Communications. 6: 10102. arXiv:1507.08901. Bibcode:2015NatCo...610102R. doi:10.1038/ncomms10102. PMC 4686770. PMID 26626302.
- ^ Sievenpiper, Dan; et al. (November 1999). "High-Impedance Electromagnetic Surfaces with a Forbidden Frequency Band" (PDF). IEEE Transactions on Microwave Theory and Techniques. 47 (11): 2059–74. Bibcode:1999ITMTT..47.2059S. doi:10.1109/22.798001. Archived from the original (PDF) on July 19, 2011. Retrieved 2009-11-11.
- ^ Pendry, John B.; David R. Smith (June 2004). "Reversing Light: Negative Refraction" (PDF). Physics Today. 57 (June 37): 2 of 9 (originally page 38 of pp. 37–45). Bibcode:2004PhT....57f..37P. doi:10.1063/1.1784272. Retrieved 2009-09-27.
- ^ Depine, Ricardo A.; Lakhtakia, Akhlesh (2004). "A new condition to identify isotropic dielectric-magnetic materials displaying negative phase velocity". Microwave and Optical Technology Letters. 41 (4): 315–16. arXiv:physics/0311029. doi:10.1002/mop.20127. S2CID 6072651.
- ^ Voznesenskaya, A. and Kabanova, D. (2012) "Analysis of Ray Tracing Through Optical Systems with Metamaterial Elements", Scientific and Technical Journal of Information Technologies, Mechanics and Optics, Volume 5, Number 12, p. 5.
- ^ a b Plum, E.; Zhou, J.; Dong, J.; Fedotov, V. A.; Koschny, T.; Soukoulis, C. M.; Zheludev, N. I. (2009). "Metamaterial with negative index due to chirality" (PDF). Physical Review B. 79 (3): 035407. Bibcode:2009PhRvB..79c5407P. doi:10.1103/PhysRevB.79.035407. S2CID 119259753.
- ^ a b Zhang, S.; Park, Y.-S.; Li, J.; Lu, X.; Zhang, W.; Zhang, X. (2009). "Negative Refractive Index in Chiral Metamaterials". Physical Review Letters. 102 (2): 023901. Bibcode:2009PhRvL.102b3901Z. doi:10.1103/PhysRevLett.102.023901. PMID 19257274.
- ^ a b c d e Eleftheriades, George V.; Keith G. Balmain (2005). Negative-refraction metamaterials: fundamental principles and applications. Wiley. p. 340. Bibcode:2005nmfp.book.....E. ISBN 978-0-471-60146-3.
- ^ Alù, Andrea and; Nader Engheta (January 2004). "Guided Modes in a Waveguide Filled With a Pair of Single-Negative (SNG), Double-Negative (DNG), and/or Double-Positive (DPS) Layers" (PDF). IEEE Transactions on Microwave Theory and Techniques. 52 (1): 199–210. Bibcode:2004ITMTT..52..199A. doi:10.1109/TMTT.2003.821274. S2CID 234001. Retrieved 2010-01-03.
- ^ High, A.; et al. (2015). "Visible-frequency hyperbolic metasurface". Nature. 522 (7555): 192–196. Bibcode:2015Natur.522..192H. doi:10.1038/nature14477. PMID 26062510. S2CID 205243865.
- ^ Pianelli, A., Kowerdziej, R., Dudek, M., Sielezin, K., Olifierczuk, M., & Parka, J. (2020). Graphene-based hyperbolic metamaterial as a switchable reflection modulator. Optics Express, 28(5), 6708–6718.https://doi.org/10.1364/OE.387065
- ^ Takayama, O.; Lavrinenko, A. V. (2019). "Optics with hyperbolic materials" (PDF). Journal of the Optical Society of America B. 36 (8): F38–F48. doi:10.1364/JOSAB.36.000F38. S2CID 149698994.
- ^ Engheta, Nader; Richard W. Ziolkowski (2006). Metamaterials: physics and engineering explorations (added this reference on 2009-12-14.). Wiley & Sons. pp. 211–21. ISBN 978-0-471-76102-0.
- ^ Valentine, J.; Zhang, S.; Zentgraf, T.; Ulin-Avila, E.; Genov, D. A.; Bartal, G.; Zhang, X. (2008). "Three-dimensional optical metamaterial with a negative refractive index". Nature. 455 (7211): 376–79. Bibcode:2008Natur.455..376V. doi:10.1038/nature07247. PMID 18690249. S2CID 4314138.
- ^ Pendry, JB (2009-04-11). "Metamaterials Generate Novel Electromagnetic Properties". UC Berkeley Atomic Physics Seminar 290F. Archived from the original (Seminar – lecture series) on 2010-06-27. Retrieved 2009-12-14.
- ^ Chappell, William leads the IDEA laboratory at Purdue University (2005). "Metamaterials". research in various technologies. Retrieved 2009-11-23.
- ^ a b Soukoulis, C. M., ed. (May 2001). Photonic Crystals and Light Localization in the 21st Century (Proceedings of the NATO Advanced Study Institute on Photonic Crystals and Light Localization, Crete, Greece, June 18–30, 2000 ed.). London: Springer London, Limited. pp. xi. ISBN 978-0-7923-6948-6.
- ^ Marques, Ricardo; Medina, Francisco; Rafii-El-Idrissi, Rachid (2002-04-04). "Role of bianisotropy in negative permeability and left-handed metamaterials" (PDF). Physical Review B. 65 (14): 144440–41. Bibcode:2002PhRvB..65n4440M. doi:10.1103/PhysRevB.65.144440. hdl:11441/59428. Archived from the original (PDF) on 20 July 2011.
- ^ Rill, M. S.; et al. (2008-12-22). "Negative-index bianisotropic photonic metamaterial fabricated by direct laser writing and silver shadow evaporation". Optics Letters. 34 (1): 19–21. arXiv:0809.2207. Bibcode:2009OptL...34...19R. doi:10.1364/OL.34.000019. PMID 19109626. S2CID 18596552.
- ^ Kriegler, C. E.; et al. (2010). "Bianisotropic photonic metamaterials" (PDF). IEEE Journal of Selected Topics in Quantum Electronics. 999 (2): 1–15. Bibcode:2010IJSTQ..16..367K. doi:10.1109/JSTQE.2009.2020809. S2CID 13854440.
- ^ Fedotov, V. A.; Mladyonov, P. L.; Prosvirnin, S. L.; Rogacheva, A. V.; Chen, Y.; Zheludev, N. I. (2006). "Asymmetric propagation of electromagnetic waves through a planar chiral structure". Physical Review Letters. 97 (16): 167401. arXiv:physics/0604234. Bibcode:2006PhRvL..97p7401F. doi:10.1103/PhysRevLett.97.167401. PMID 17155432. S2CID 119436346.
- ^ Plum, E.; Fedotov, V. A.; Zheludev, N. I. (2009). "Planar metamaterial with transmission and reflection that depend on the direction of incidence". Applied Physics Letters. 94 (13): 131901. arXiv:0812.0696. Bibcode:2009ApPhL..94m1901P. doi:10.1063/1.3109780. S2CID 118558819.
- ^ Plum, E.; Liu, X.-X.; Fedotov, V. A.; Chen, Y.; Tsai, D. P.; Zheludev, N. I. (2009). "Metamaterials: Optical Activity without Chirality" (PDF). Phys. Rev. Lett. 102 (11): 113902. Bibcode:2009PhRvL.102k3902P. doi:10.1103/physrevlett.102.113902. PMID 19392202.
- ^ Ren, M.; Plum, E.; Xu, J.; Zheludev, N. I. (2012). "Giant nonlinear optical activity in a plasmonic metamaterial". Nature Communications. 3: 833. Bibcode:2012NatCo...3..833R. doi:10.1038/ncomms1805. PMID 22588295.
- ^ Plum, E.; Fedotov, V. A.; Zheludev, N. I. (2016). "Specular optical activity of achiral metasurfaces" (PDF). Applied Physics Letters. 108 (14): 141905. Bibcode:2016ApPhL.108n1905P. doi:10.1063/1.4944775. hdl:10220/40854.
- ^ Plum, E.; Fedotov, V. A.; Zheludev, N. I. (2009). "Extrinsic electromagnetic chirality in metamaterials". Journal of Optics A: Pure and Applied Optics. 11 (7): 074009. Bibcode:2009JOptA..11g4009P. doi:10.1088/1464-4258/11/7/074009.
- ^ C. Rizza; Andrea Di Falco; Michael Scalora & Alessandro Ciattoni (2015). "One-Dimensional Chirality: Strong Optical Activity in Epsilon-Near-Zero Metamaterials". Phys. Rev. Lett. 115 (5): 057401. arXiv:1503.00490. Bibcode:2015PhRvL.115e7401R. doi:10.1103/PhysRevLett.115.057401. PMID 26274441. S2CID 11708854.
- ^ Wang, Bingnan; et al. (November 2009). "Chiral metamaterials: simulations and experiments". J. Opt. Soc. Am. A. 11 (11): 114003. Bibcode:2009JOptA..11k4003W. doi:10.1088/1464-4258/11/11/114003.
- ^ Tretyakov, S.; Sihvola, A.; Jylhä, L. (2005). "Backward-wave regime and negative refraction in chiral composites". Photonics and Nanostructures: Fundamentals and Applications. 3 (2–3): 107–15. arXiv:cond-mat/0509287. Bibcode:2005PhNan...3..107T. doi:10.1016/j.photonics.2005.09.008. S2CID 118914130.
- ^ Capolino, Filippo (2009). "Chapter 32". Theory and Phenomena of Metamaterials. Taylor & Francis. ISBN 978-1-4200-5425-5.
- ^ Page, John (2011). "Metamaterials: Neither solid nor liquid". Nature Materials. 10 (8): 565–66. Bibcode:2011NatMa..10..565P. doi:10.1038/nmat3084. PMID 21778996.
- ^ Szondy, David (June 22, 2014). "New materials developed that are as light as aerogel, yet 10,000 times stronger". Gizmag.
- ^ Fang, Nicholas. "Projection Microstereolithography" (PDF). Department of Mechanical Science & Engineering, University of Illinois.
- ^ Fesenmaier, Kimm (23 May 2014). "Miniature Truss Work". Caltech.
- ^ Ciattoni, A.; Rizza, C.; Palange, E. (2010). "Extreme nonlinear electrodynamics in metamaterials with very small linear dielectric permittivity". Phys. Rev. A. 81 (4): 043839. arXiv:1002.3321. Bibcode:2010PhRvA..81d3839C. doi:10.1103/PhysRevA.81.043839. S2CID 119182809.
- ^ Vincenti, M. A.; De Ceglia, D.; Ciattoni, A.; Scalora, M. (2011). "Singularity-driven second- and third-harmonic generation at epsilon-near-zero crossing points". Phys. Rev. A. 84 (6): 063826. arXiv:1107.2354. Bibcode:2011PhRvA..84f3826V. doi:10.1103/PhysRevA.84.063826. S2CID 55294978.
- ^ Capretti, Antonio; Wang, Yu; Engheta, Nader; Dal Negro, Luca (2015). "Enhanced third-harmonic generation in Si-compatible epsilon-near-zero indium tin oxide nanolayers". Opt. Lett. 40 (7): 1500–3. Bibcode:2015OptL...40.1500C. doi:10.1364/OL.40.001500. PMID 25831369.
- ^ Irving, Michael (April 9, 2024). "Harvard's bizarre "metafluid" packs programmable properties". New Atlas. Retrieved 2024-04-12.
- ^ Briane, Marc; Milton, Graeme W. (28 November 2008). "Homogenization of the Three-dimensional Hall Effect and Change of Sign of the Hall Coefficient" (PDF). Archive for Rational Mechanics and Analysis. 193 (3): 715–736. doi:10.1007/s00205-008-0200-y. S2CID 9367952.
- ^ Kadic, Muamer; Schittny, Robert; Bückmann, Tiemo; Kern, Christian; Wegener, Martin (22 June 2015). "Hall-Effect Sign Inversion in a Realizable 3D Metamaterial". Physical Review X. 5 (2): 021030. arXiv:1503.06118. Bibcode:2015PhRvX...5b1030K. doi:10.1103/PhysRevX.5.021030. S2CID 55414502.
- ^ Kern, Christian; Kadic, Muamer; Wegener, Martin (2017). "Experimental Evidence for Sign Reversal of the Hall Coefficient in Three-Dimensional Metamaterials". Physical Review Letters. 118 (1): 016601. Bibcode:2017PhRvL.118a6601K. doi:10.1103/PhysRevLett.118.016601. PMID 28106428.
- ^ Kern, Christian; Kadic, Muamer; Wegener, Martin (28 September 2015). "Parallel Hall effect from three-dimensional single-component metamaterials". Applied Physics Letters. 107 (13): 132103. arXiv:1507.04128. Bibcode:2015ApPhL.107m2103K. doi:10.1063/1.4932046. S2CID 119261088.
- ^ Abdeddaim, R.; Lecoq, P.; Enoch, S. (2019-04-30). "Metamaterials: opportunities in medical imaging". Metamaterials XII. 11025. SPIE: 29–35. doi:10.1117/12.2523340.
- ^ Zadpoor, Amir A. (2019-12-17). "Meta-biomaterials". Biomaterials Science. 8 (1): 18–38. doi:10.1039/C9BM01247H. ISSN 2047-4849.
- ^ Grebenyuk, Sergei; Abdel Fattah, Abdel Rahman; Kumar, Manoj; Toprakhisar, Burak; Rustandi, Gregorius; Vananroye, Anja; Salmon, Idris; Verfaillie, Catherine; Grillo, Mark; Ranga, Adrian (2023-01-12). "Large-scale perfused tissues via synthetic 3D soft microfluidics". Nature Communications. 14 (1): 193. doi:10.1038/s41467-022-35619-1. ISSN 2041-1723. PMC 9837048.
- ^ Paschotta, Rüdiger (2008–18). "Photonic Metamaterials". Encyclopedia of Laser Physics and Technology. Vol. I & II. Wiley-VCH Verlag. p. 1. Retrieved 2009-10-01.
- ^ Capolino, Filippo (2009). Applications of Metamaterials. Taylor & Francis, Inc. pp. 29–1, 25–14, 22–1. ISBN 978-1-4200-5423-1. Retrieved 2009-10-01.
- ^ Takayama, O.; Bogdanov, A. A., Lavrinenko, A. V. (2017). "Photonic surface waves on metamaterial interfaces". Journal of Physics: Condensed Matter. 29 (46): 463001. Bibcode:2017JPCM...29T3001T. doi:10.1088/1361-648X/aa8bdd. PMID 29053474. S2CID 1528860.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ Bormashenko, Edward; Legchenkova, Irina (January 2020). "Negative Effective Mass in Plasmonic Systems". Materials. 13 (8): 1890. Bibcode:2020Mate...13.1890B. doi:10.3390/ma13081890. PMC 7215794. PMID 32316640.
- ^ Bormashenko, Edward; Legchenkova, Irina; Frenkel, Mark (January 2020). "Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation". Materials. 13 (16): 3512. Bibcode:2020Mate...13.3512B. doi:10.3390/ma13163512. PMC 7476018. PMID 32784869.
- ^ Oliveri, G.; Werner, D.H.; Massa, A. (2015). "Reconfigurable electromagnetics through metamaterials – A review". Proceedings of the IEEE. 103 (7): 1034–56. doi:10.1109/JPROC.2015.2394292. S2CID 25179597.
- ^ Costas Soukoulis (2007-01-04). "Metamaterials found to work for visible light". DOE /Ames Laboratory. Retrieved 2009-11-07.
- ^ Enoch, Stefan; Tayeb, GéRard; Sabouroux, Pierre; Guérin, Nicolas; Vincent, Patrick (2002). "A Metamaterial for Directive Emission". Physical Review Letters. 89 (21): 213902. Bibcode:2002PhRvL..89u3902E. doi:10.1103/PhysRevLett.89.213902. PMID 12443413. S2CID 37505778.
- ^ Siddiqui, O.F.; Mo Mojahedi; Eleftheriades, G.V. (2003). "Periodically loaded transmission line with effective negative refractive index and negative group velocity". IEEE Transactions on Antennas and Propagation. 51 (10): 2619–25. Bibcode:2003ITAP...51.2619S. doi:10.1109/TAP.2003.817556.
- ^ Wu, B.-I.; W. Wang, J. Pacheco, X. Chen, T. Grzegorczyk and J. A. Kong; Pacheco, Joe; Chen, Xudong; Grzegorczyk, Tomasz M.; Kong, Jin Au (2005). "A Study of Using Metamaterials as Antenna Substrate to Enhance Gain". Progress in Electromagnetics Research. 51: 295–28. doi:10.2528/PIER04070701.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ^ de Oliveira Neto, A. M.; Beccaro, W.; de Oliveira, A. M.; Justo, J.F. (2023). "Exploring the Internal Patterns in the Design of Ultrawideband Microwave Absorbers". IEEE Antennas and Wireless Propagation Letters. 22 (9): 2290–2294. doi:10.1109/LAWP.2023.3284650.
- ^ Li, W.; Valentine, J. (2014). "Metamaterial Perfect Absorber Based Hot Electron Photodetection". Nano Letters. 14 (6): 3510–14. Bibcode:2014NanoL..14.3510L. doi:10.1021/nl501090w. PMID 24837991.
- ^ Yu, Peng; Wu, Jiang; Ashalley, Eric; Govorov, Alexander; Wang, Zhiming (2016). "Dual-band absorber for multispectral plasmon-enhanced infrared photodetection" (PDF). Journal of Physics D: Applied Physics. 49 (36): 365101. Bibcode:2016JPhD...49J5101Y. doi:10.1088/0022-3727/49/36/365101. ISSN 0022-3727. S2CID 123927835.
- ^ Yu, Peng; Besteiro, Lucas V.; Huang, Yongjun; Wu, Jiang; Fu, Lan; Tan, Hark H.; Jagadish, Chennupati; Wiederrecht, Gary P.; Govorov, Alexander O. (2018). "Broadband Metamaterial Absorbers". Advanced Optical Materials. 7 (3): 1800995. doi:10.1002/adom.201800995. hdl:1885/213159. ISSN 2195-1071.
- ^ Pendry, J. B. (2000). "Negative Refraction Makes a Perfect Lens". Physical Review Letters. 85 (18): 3966–69. Bibcode:2000PhRvL..85.3966P. doi:10.1103/PhysRevLett.85.3966. PMID 11041972. S2CID 25803316.
- ^ Fang, N.; Lee, H; Sun, C; Zhang, X (2005). "Sub-Diffraction-Limited Optical Imaging with a Silver Superlens". Science. 308 (5721): 534–37. Bibcode:2005Sci...308..534F. doi:10.1126/science.1108759. PMID 15845849. S2CID 1085807.
- ^ "First Demonstration of a Working Invisibility Cloak". Office of News & Communications Duke University. Archived from the original on July 19, 2009. Retrieved 2009-05-05.
- ^ Schurig, D.; et al. (2006). "Metamaterial Electromagnetic Cloak at Microwave Frequencies". Science. 314 (5801): 977–80. Bibcode:2006Sci...314..977S. doi:10.1126/science.1133628. PMID 17053110. S2CID 8387554.
- ^ "Experts test cloaking technology". BBC News. 2006-10-19. Retrieved 2008-08-05.
- ^ "Engineers see progress in creating 'invisibility cloak'". purdue.edu.
- ^ Alù, Andrea; Engheta, Nader (2005). "Achieving transparency with plasmonic and metamaterial coatings". Phys. Rev. E. 72 (1): 016623. arXiv:cond-mat/0502336. Bibcode:2005PhRvE..72a6623A. doi:10.1103/PhysRevE.72.016623. PMID 16090123. S2CID 6004609.
- ^ Merritt, Richard (January 2009) "Next Generation Cloaking Device Demonstrated: Metamaterial renders object 'invisible'" Archived February 20, 2009, at the Wayback Machine
- ^ Modi, A. Y.; Alyahya, M. A.; Balanis, C. A.; Birtcher, C. R. (2019). "Metasurface-Based Method for Broadband RCS Reduction of Dihedral Corner Reflectors with Multiple Bounces". IEEE Transactions on Antennas and Propagation. 67 (3): 1. doi:10.1109/TAP.2019.2940494. S2CID 212649480.
- ^ Modi, A. Y.; Balanis, C. A.; Birtcher, C. R.; Shaman, H. (2019). "New Class of RCS-Reduction Metasurfaces Based on Scattering Cancellation Using Array Theory". IEEE Transactions on Antennas and Propagation. 67 (1): 298–308. Bibcode:2019ITAP...67..298M. doi:10.1109/TAP.2018.2878641. S2CID 58670543.
- ^ Modi, Anuj Y.; Balanis, Constantine A.; Birtcher, Craig R.; Shaman, Hussein N. (2017). "Novel Design of Ultrabroadband Radar Cross Section Reduction Surfaces Using Artificial Magnetic Conductors". IEEE Transactions on Antennas and Propagation. 65 (10): 5406–5417. Bibcode:2017ITAP...65.5406M. doi:10.1109/TAP.2017.2734069. S2CID 20724998.
- ^ MarÃ; de Cos, Elena; Alvarez Lopez, Yuri; Las-Heras, Fernando (2010). "A novel approach for RCS reduction using a combination of artificial magnetic conductors". Progress in Electromagnetics Research. 107: 147–159. doi:10.2528/PIER10060402.
- ^ Li, Yongfeng; Zhang, Jieqiu; Qu, Shaobo; Wang, Jiafu; Chen, Hongya; Xu, Zhuo; Zhang, Anxue (2014). "Wideband radar cross section reduction using two-dimensional phase gradient metasurfaces". Applied Physics Letters. 104 (22): 221110. Bibcode:2014ApPhL.104v1110L. doi:10.1063/1.4881935.
- ^ Yu, Nanfang; Genevet, Patrice; Kats, Mikhail A.; Aieta, Francesco; Tetienne, Jean-Philippe; Capasso, Federico; Gaburro, Zeno (October 2011). "Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction". Science. 334 (6054): 333–7. Bibcode:2011Sci...334..333Y. doi:10.1126/science.1210713. PMID 21885733. S2CID 10156200.
- ^ Johnson, R. Colin (2009-07-23). "Metamaterial cloak could render buildings 'invisible' to earthquakes". EETimes.com. Retrieved 2009-09-09.
- ^ Barras, Colin (2009-06-26). "Invisibility cloak could hide buildings from quakes". New Scientist. p. 1. Retrieved 2009-10-20.
- ^ "Wrinkled metamaterials for controlling light and sound propagation". KurzweilAI. 2014-01-28. Retrieved 2014-04-15.
- ^ Rudykh, S.; Boyce, M. C. (2014). "Transforming Wave Propagation in Layered Media via Instability-Induced Interfacial Wrinkling". Physical Review Letters. 112 (3): 034301. Bibcode:2014PhRvL.112c4301R. doi:10.1103/PhysRevLett.112.034301. hdl:1721.1/85082. PMID 24484141.
- ^ a b Meng, Yuan; Chen, Yizhen; Lu, Longhui; Ding, Yimin; Cusano, Andrea; Fan, Jonathan A.; Hu, Qiaomu; Wang, Kaiyuan; Xie, Zhenwei; Liu, Zhoutian; Yang, Yuanmu (2021-11-22). "Optical meta-waveguides for integrated photonics and beyond". Light: Science & Applications. 10 (1): 235. Bibcode:2021LSA....10..235M. doi:10.1038/s41377-021-00655-x. ISSN 2047-7538. PMC 8608813. PMID 34811345.
- ^ Halir, Robert; Cheben, Pavel; Luque-González, José Manuel; Sarmiento-Merenguel, Jose Darío; Schmid, Jens H.; Wangüemert-Pérez, Gonzalo; Xu, Dan-Xia; Wang, Shurui; Ortega-Moñux, Alejandro; Molina-Fernández, Íñigo (November 2016). "Ultra-broadband nanophotonic beamsplitter using an anisotropic sub-wavelength metamaterial". Laser & Photonics Reviews. 10 (6): 1039–1046. arXiv:1606.03750. Bibcode:2016LPRv...10.1039H. doi:10.1002/lpor.201600213. ISSN 1863-8880. S2CID 126025926.
- ^ Meng, Yuan; Hu, Futai; Liu, Zhoutian; Xie, Peng; Shen, Yijie; Xiao, Qirong; Fu, Xing; Bae, Sang-Hoon; Gong, Mali (2019-06-10). "Chip-integrated metasurface for versatile and multi-wavelength control of light couplings with independent phase and arbitrary polarization". Optics Express. 27 (12): 16425–16439. Bibcode:2019OExpr..2716425M. doi:10.1364/OE.27.016425. ISSN 1094-4087. PMID 31252868. S2CID 189958968.
- ^ Cheben, Pavel; Halir, Robert; Schmid, Jens H.; Atwater, Harry A.; Smith, David R. (August 2018). "Subwavelength integrated photonics". Nature. 560 (7720): 565–572. Bibcode:2018Natur.560..565C. doi:10.1038/s41586-018-0421-7. ISSN 1476-4687. PMID 30158604. S2CID 52117964.
- ^ Li, Zhaoyi; Kim, Myoung-Hwan; Wang, Cheng; Han, Zhaohong; Shrestha, Sajan; Overvig, Adam Christopher; Lu, Ming; Stein, Aaron; Agarwal, Anuradha Murthy; Lončar, Marko; Yu, Nanfang (July 2017). "Controlling propagation and coupling of waveguide modes using phase-gradient metasurfaces". Nature Nanotechnology. 12 (7): 675–683. Bibcode:2017NatNa..12..675L. doi:10.1038/nnano.2017.50. ISSN 1748-3395. OSTI 1412777. PMID 28416817.
- ^ Guo, Rui; Decker, Manuel; Setzpfandt, Frank; Gai, Xin; Choi, Duk-Yong; Kiselev, Roman; Chipouline, Arkadi; Staude, Isabelle; Pertsch, Thomas; Neshev, Dragomir N.; Kivshar, Yuri S. (2017-07-07). "High–bit rate ultra-compact light routing with mode-selective on-chip nanoantennas". Science Advances. 3 (7): e1700007. Bibcode:2017SciA....3E0007G. doi:10.1126/sciadv.1700007. ISSN 2375-2548. PMC 5517110. PMID 28776027.
- ^ He, Tiantian; Meng, Yuan; Liu, Zhoutian; Hu, Futai; Wang, Rui; Li, Dan; Yan, Ping; Liu, Qiang; Gong, Mali; Xiao, Qirong (2021-11-22). "Guided mode meta-optics: metasurface-dressed waveguides for arbitrary mode couplers and on-chip OAM emitters with a configurable topological charge". Optics Express. 29 (24): 39406–39418. Bibcode:2021OExpr..2939406H. doi:10.1364/OE.443186. ISSN 1094-4087. PMID 34809306. Retrieved 2023-02-22.
- ^ Flueckiger, Jonas; Schmidt, Shon; Donzella, Valentina; Sherwali, Ahmed; Ratner, Daniel M.; Chrostowski, Lukas; Cheung, Karen C. (2016-07-11). "Sub-wavelength grating for enhanced ring resonator biosensor". Optics Express. 24 (14): 15672–15686. Bibcode:2016OExpr..2415672F. doi:10.1364/OE.24.015672. ISSN 1094-4087. PMID 27410840.
- ^ Shore, R. A.; Yaghjian, A. D. (2007). "Traveling waves on two- and three-dimensional periodic arrays of lossless scatterers". Radio Science. 42 (6): RS6S21. Bibcode:2007RaSc...42.6S21S. doi:10.1029/2007RS003647.
- ^ Li, Y.; Bowler, N. (2012). "Traveling waves on three-dimensional periodic arrays of two different magnetodielectric spheres arbitrarily arranged on a simple tetragonal lattice". IEEE Transactions on Antennas and Propagation. 60 (6): 2727–39. Bibcode:2012ITAP...60.2727L. doi:10.1109/tap.2012.2194637. S2CID 21023639.
- ^ MURI metamaterials, UC Berkeley (2009). "Scalable and Reconfigurable Electromagnetic Metamaterials and Devices". Archived from the original on 2009-12-03. Retrieved 2009-12-08.
- ^ U.S. Department of Defense, Office of the Assistant Secretary of Defense (Public Affairs) (2009-05-08). "DoD Awards $260 Million in University Research Funding". DoD. Archived from the original on March 2, 2010. Retrieved 2009-12-08.
- ^
Tretyakov, Prof. Sergei; President of the Association; Dr. Vladmir Podlozny; Secretary General (2009-12-13). "Metamorphose" (See the "About" section of this web site for information about this organization.). Metamaterials research and development. Metamorphose VI. Retrieved 2009-12-13.
{{cite web}}: CS1 maint: multiple names: authors list (link) - ^ de Baas, A. F.; J. L. Vallés (2007-02-11). "Success stories in the Materials domain" (PDF). Metamorphose. Networks of Excellence Key for the future of EU research: 19. Retrieved 2009-12-13.
External links[edit]
 Media related to Metamaterials at Wikimedia Commons
Media related to Metamaterials at Wikimedia Commons























