Jump to content

Speed of light: Difference between revisions

Edit links
From Wikipedia, the free encyclopedia
Browse history interactively
← Previous editNext edit →
Content deleted Content added
VisualWikitext
m →Astronomy: reword to fix weird tense
Avalcarce (talk | contribs)
40 edits
No edit summary
Line 672: Line 672:


If the refractive index of a material depends on the frequency of the light passing through the medium, there exist two notions of the speed of light in the medium. The first is the speed of a wave of a [[monochromatic light|single frequency]] ''f''. This is called the [[phase velocity]] ''v<sub>p</sub>(f)'', and is related to the frequency dependent refractive index ''n(f)'' by
If the refractive index of a material depends on the frequency of the light passing through the medium, there exist two notions of the speed of light in the medium. The first is the speed of a wave of a [[monochromatic light|single frequency]] ''f''. This is called the [[phase velocity]] ''v<sub>p</sub>(f)'', and is related to the frequency dependent refractive index ''n(f)'' by
:<math> v_p = c\ n(f).</math>
:<math> v_p = c / n(f).</math>
The second is the average velocity of a pulse of light consisting of different frequencies of light. This is called the [[group velocity]] and not only depends on the properties of the medium but also the distribution of frequencies in the pulse. A pulse with different group and phase velocities is said to undergo [[Dispersion (optics)|dispersion]].
The second is the average velocity of a pulse of light consisting of different frequencies of light. This is called the [[group velocity]] and not only depends on the properties of the medium but also the distribution of frequencies in the pulse. A pulse with different group and phase velocities is said to undergo [[Dispersion (optics)|dispersion]].


Revision as of 10:29, 2 February 2010

"Light barrier" redirects here. For the device, see Photoelectric sensor.

Template:Otheruses6

The Earth orbits the Sun at a distance of 150 million kilometres, and the Moon in turn orbits the Earth.
Sunlight takes about 8 minutes, 19 seconds to reach Earth.
Speed of light in different units
metres per second 299,792,458 (exact)
kilometres per second ≈ 300,000
kilometres per hour ≈ 1,079 million
miles per second ≈ 186,000
miles per hour ≈ 671 million
astronomical units per day ≈ 173
Planck units 1 (exact)
Approximate length of time for light to travel:
One foot 1.0 ns
One metre 3.3 ns
One kilometre 3.3 μs
One statute mile 5.4 μs
To Earth from geostationary orbit 119 ms
The length of Earth's equator 134 ms
To Earth from the Moon 1.3 s
To Earth from the Sun 8.3 min
One parsec 3.26 years
To Earth from Alpha Centauri 4.4 years
Across the Milky Way 100,000 years
To Earth from the Andromeda Galaxy 2.5 million years

The speed of light (usually denoted c) is a physical constant. Its value is exactly 299,792,458 metres per second,[1][2] often approximated as 300,000 kilometres per second or 186,000 miles per second (see the table on the right for values in other units). It is the speed of electromagnetic radiation (such as radio waves, visible light, or gamma rays) in vacuum, where there are no atoms, molecules or other types of matter that can slow it down.

For much of human history, it was not known whether light was transmitted instantaneously or simply very quickly. In the 17th century, Ole Rømer first demonstrated that it travelled at a finite speed by studying the apparent motion of Jupiter's moon Io. By 1975, the speed of light was known to be 299792458 m/s with a relative measurement uncertainty of 4 parts per billion. In 1983, the metre was redefined in the International System of Units (SI) as the distance travelled by light in vacuum in 1⁄299792458 of a second. As a result, the numerical value of c in metres per second is now fixed exactly by the definition of the metre.[1][2]

According to the theory of special relativity, c connects space and time in the unified structure of spacetime, and its square is the constant of proportionality between mass and energy (E = mc2).[3] In any inertial frame of reference, independently of the relative velocity of the emitter and the observer, c is the speed of all massless particles and associated fields, including all electromagnetic radiation in free space,[4] and it is believed to be the speed of gravity and of gravitational waves.[5][6] It is an upper bound on the speed at which energy, matter, and information can travel,[7][8] as surpassing it "would lead to the destruction of the essential relation between cause and effect."[9] Its finite value is a limiting factor in the speed of operation of electronic devices.[10]

The actual speed at which light propagates through transparent materials, such as glass or air, is less than c. The ratio between c and the speed v at which light travels in a material is called the refractive index n of the material (n = c / v). For example, for visible light the refractive index of glass is typically around 1.5, meaning that light in glass travels at c / 1.5 ≈ 200000 km/s; the refractive index of air for visible light is about 1.0003, so the speed of light in air is very close to c.

Numerical value, notation and units

The speed of light is a dimensional physical constant, so its numerical value depends on the system of units used. In the International System of Units (SI), the metre is defined as the distance light travels in vacuum in 1⁄299792458 of a second (see "{{Section link}}: required section parameter(s) missing", below). The effect of this definition is to fix the speed of light in vacuum at exactly 299792458 m/s.[Note 1][12][13][14]

The speed of light in vacuum is usually denoted by c, for "constant" or the Latin [celeritas] Error: {{Lang}}: text has italic markup (help) (meaning "swiftness"). Originally, the symbol V was used, introduced by Maxwell in 1865. In 1856, Weber and Kohlrausch had used c for a constant later shown to equal √2 times the speed of light in vacuum. In 1894, Drude redefined c with its modern meaning. Einstein used V in his original German-language papers on special relativity in 1905, but in 1907 he switched to c, which by then had become the standard symbol.[15][16]

Some authors use c for the speed of waves in any material medium, and c0 for the speed of light in vacuum.[17] This subscripted notation, which is endorsed in official SI literature,[1] has the same form as other related constants: namely, μ0 for the vacuum permeability or magnetic constant, ε0 for the vacuum permittivity or electric constant, and Z0 for the impedance of free space. This article uses c exclusively for the speed of light in vacuum.

In branches of physics in which the speed of light plays an important part, such as in relativity, it is common to use systems of natural units of measurement in which c = 1.[18][19] When such a system of measurement is used, the speed of light drops out of the equations of physics, because multiplication or division by 1 does not affect the result.

Fundamental role in physics

See also: Introduction to special relativity and Special relativity

The speed at which light propagates in vacuum is independent both of the motion of the light source and of the inertial frame of reference of the observer.[Note 2] The constancy of the speed of light was postulated by Albert Einstein in 1905, motivated by Maxwell's theory of electromagnetism and the lack of evidence for the luminiferous ether;[20] it has since been consistently confirmed by many experiments.[Note 3] [19][21] The theory of special relativity explores the consequences an invariant speed c and the assumption that the laws of physics are the same in all inertial frames of reference.[22][23] One consequence is that c is the speed at which all massless particles and waves, including light, must travel.

Three pairs of coordinate axes are depicted with the same origin A; in the green frame, the x axis is horizontal and the ct axis is vertical; in the red frame, the x′ axis is slightly skewed upwards, and the ct′ axis slightly skewed rightwards, relative to the green axes; in the blue frame, the x′′ axis is somewhat skewed downwards, and the ct′′ axis somewhat skewed leftwards, relative to the green axes. A point B on the green x axis, to the left of A, has zero ct, positive ct′, and negative ct′′.
Event A precedes B in the red frame, is simultaneous with B in the green frame, and follows B in the blue frame.

Special relativity has many counter-intuitive implications, but they have been verified in many experiments.[24] These include the equivalence of mass and energy (E = mc2), length contraction (moving objects shorten),[Note 4] and time dilation (moving clocks run slower). Length contraction and time dilation are negligible for speeds much slower than c, such as most everyday speeds, in which case special relativity is closely approximated by Galilean relativity.

Another counter-intuitive consequence of special relativity is the relativity of simultaneity: if the spatial distance between two events A and B is greater than the time interval between them multiplied by c, then there are frames of reference in which A precedes B, others in which B precedes A, and others in which they are simultaneous. Such events cannot have a causal relation.

The results of special relativity can be summarized by treating space and time as a unified structure known as spacetime (with c relating the units of space and time), and requiring that physical theories satisfy a special symmetry called Lorentz invariance, whose mathematical formulation contains the parameter c.[27] Lorentz invariance has become an almost universal assumption for modern physical theories, such as quantum electrodynamics, quantum chromodynamics, the Standard Model of particle physics, and general relativity. As such, the parameter c is ubiquitous in modern physics, appearing in many contexts that may seem to be unrelated to light. For example, general relativity predicts that c is also the speed of gravity and of gravitational waves.[28]

In non-inertial frames of reference (gravitationally curved space or accelerated reference frames), the local speed of light is constant and equal to c, but the speed of light along a trajectory of finite length can differ from c, depending on how distances and times are defined.[29]

It is generally assumed in physics that fundamental constants such as c have the same value throughout spacetime, meaning that they do not depend on location and do not vary with time. However, various theories have suggested that the speed of light has changed over time.[30][31] Although no conclusive evidence for such theories has been found, they remain the subject of ongoing research.[32][33][34]

Upper limit on speeds

See also: Chronology protection conjecture
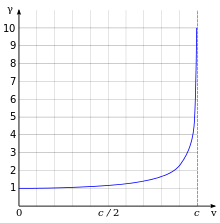
γ starts at 1 when v equals zero and stays nearly constant for small v's, then it sharply curves upwards and has a vertical asymptote, diverging to positive infinity as v approaches c.
The Lorentz factor γ as a function of velocity. It starts at value 1 and goes to infinity as v approaches c.

According to special relativity, the energy of an object with rest mass m and speed v is given by γmc2, where γ = (1 − v2/c2)−1/2 is the Lorentz factor. When v is zero, γ is equal to one, giving rise to the famous E = mc2 formula for mass-energy equivalence. The γ factor grows rapidly with v and approaches infinity as v approaches c. It would thus take an infinite amount of energy to accelerate an object with mass to the speed of light. The speed of light is the upper limit for the speeds of objects with non-zero rest mass.

More generally, it is normally impossible for any information or energy to travel faster than c. One reason is that according to the theory of special relativity, if something were travelling faster than c relative to an inertial frame of reference, it would be travelling backwards in time relative to another frame,[Note 5] and causality would be violated.[Note 6][9] In such a frame of reference, an "effect" could be observed before its "cause". Such a violation of causality has never been recorded,[21] and would lead to paradoxes.[Note 7][36]

Faster-than-light observations and experiments

Main article: Faster-than-light
See also: Scharnhorst effect and Hartman effect

There are situations in which it may seem that matter, energy, or information travels at speeds greater than c, but they do not. For example, if a laser beam is swept quickly across a distant object, the spot of light can move faster than c, but the only physical entities that are moving are the laser and its emitted light that travels at the speed c from the laser to the various positions of the spot. The movement of the spot will be delayed after the laser is moved because of the time it takes light to get to the distant object from the laser. Similarly, a shadow projected onto a distant object can be made to move faster than c.[37] In neither case does any matter or information travel faster than light.[38]

In some interpretations of quantum mechanics, certain quantum effects may seem to be transmitted faster than c– and thus instantaneously in some frame – as in the EPR paradox. An example involves the quantum states of two particles that can be entangled. Until either of the particles is observed, they exist in a superposition of two quantum states. If the particles are separated and one particle's quantum state is observed, the other particle's quantum state is determined instantaneously (i.e., faster than light could travel from one particle to the other). However, it is impossible to control which quantum state the first particle will take on when it is observed, so information cannot be transmitted in this manner.[38][39]

Another prediction of faster-than-light speeds occurs for quantum tunnelling and is called the Hartman effect.[40][41] However, no information can be sent using this effect.[42]

Closing speeds and proper speeds are examples of calculated speeds that may have value in excess of c but that do not represent the speed of an object as measured in a single inertial frame.

So-called superluminal motion is seen in certain astronomical objects,[43] such as the jets of radio galaxies and quasars. However, these jets are not moving at speeds in excess of the speed of light: the apparent superluminal motion is a projection effect caused by objects moving near the speed of light and approaching Earth at a small angle to the line of sight: since the light which was emitted when the jet was farther away took longer to reach the Earth, the time between two successive observations corresponds to a longer time between the instants at which the light rays were emitted.[44]

Galaxies moving faster than light
See also: Metric expansion of space and Hubble's Law

In models of the expanding universe, the farther galaxies are from each other, the faster they drift apart. This receding is not due to motion through space, but rather to the expansion of space itself.[38] For example, galaxies far away from Earth appear to be moving away from the Earth with a speed proportional to their distances. Beyond a boundary called the Hubble sphere, this apparent recessional velocity becomes greater than the speed of light.

Propagation of light

In classical physics, light is described as a type of electromagnetic wave. The classical behaviour of the electromagnetic field is described by Maxwell's equations, which predict that the speed c with which electromagnetic waves (such as light) propagate through the vacuum is related to the electric constant ε0 and the magnetic constant μ0 by the equation c = 1/√ε0μ0.[45]

In modern quantum physics, the electromagnetic field is described by the theory of quantum electrodynamics (QED). In this theory, light is described by the fundamental excitations (or quanta) of the electromagnetic field, called photons. In QED, photons are massless particles and thus, according to special relativity, they must travel at the speed of light.

Extensions of QED in which the photon has a mass have been considered. In such a theory, its speed would depend on its frequency, and the invariant speed c of special relativity would then be the upper limit of the speed of light in vacuum.[29] To date no such effects have been observed,[46][47][48] putting stringent limits on the photon mass. The limit obtained depends on the used model: if the massive photon is described by Proca theory,[49] the experimental upper bound for its mass is about 10−57 grams.[50] If photon mass is generated by a Higgs mechanism, the experimental upper limit is less sharp, m ≤ 10−14 eV/c2 [49] (roughly 2 × 10−47 g).

Another reason for the speed of light to vary with its frequency would be the failure of special relativity to apply to arbitrarily small scales, as predicted by some proposed theories of quantum gravity. In 2009, the observation of the spectrum of gamma-ray burst GRB 090510 did not find any difference in the speeds of photons of different energies, confirming that Lorentz invariance is verified at least down to the scale of the Planck length (lP = √ħG/c3 ≈ 1.6163×10−35 m) divided by 1.2.[51]

In a medium

See also: Refractive index and Dispersion (optics)
A white beam of light enters a prism and a spectrum comes out of it.
The light passing through a prism demonstrates refraction and, by the splitting of white light into a spectrum of colours, dispersion.

When light enters materials, its energy is absorbed. In the case of transparent materials, this energy is quickly re-radiated. However, this absorption and re-radiation introduces a delay. As light propagates through dielectric material it undergoes continuous absorption and re-radiation. Therefore when the speed of light in a medium is said to be less than c, this should be read as the speed of energy propagation at the macroscopic level. At an atomic level, electromagnetic waves always travel at c in the empty space between atoms. Two factors influence this slowing; stronger absorption leading to shorter path length between each re-radiation cycle and longer delays. The slowing is therefore the product of these two factors.[52] The refractive index of a transparent material is defined as the ratio of c to the speed of light v in the material. Larger indexes of refraction indicate smaller speeds. The refractive index of a material may depend on the light's frequency, intensity, polarization, or direction of propagation. In many cases, though, it can be treated as a material-dependent constant. The refractive index of air is approximately 1.0003.[53] Denser media, such as water and glass, have refractive indexes of around 1.3 and 1.5 respectively for visible light. Diamond has a refractive index of about 2.4.

If the refractive index of a material depends on the frequency of the light passing through the medium, there exist two notions of the speed of light in the medium. The first is the speed of a wave of a single frequency f. This is called the phase velocity vp(f), and is related to the frequency dependent refractive index n(f) by

The second is the average velocity of a pulse of light consisting of different frequencies of light. This is called the group velocity and not only depends on the properties of the medium but also the distribution of frequencies in the pulse. A pulse with different group and phase velocities is said to undergo dispersion.

Certain materials have an exceptionally low group velocity for light waves, a phenomenon called slow light. In 1999, a team of scientists led by Lene Hau were able to slow the speed of a light pulse to about 17 metres per second (61 km/h; 38 mph);[54] in 2001, they were able to momentarily stop a beam.[55] In 2003, scientists at Harvard University and the Lebedev Physical Institute in Moscow, succeeded in completely halting light by directing it into a Bose–Einstein condensate of the element rubidium, the atoms of which, in Lukin's words, behaved "like tiny mirrors" due to an interference pattern in two "control" beams.[56][57]

It is also possible for the group velocity of light pulses to exceed c.[58] In an experiment in 2000, laser beams travelled for extremely short distances through caesium atoms with a group velocity of 300 times c.[59] It is not possible to transmit information faster than c by this means because the speed of information transfer cannot exceed the front velocity of the wave pulse, which is always less than c.[60] The requirement that causality is not violated implies that the real and imaginary parts of the dielectric constant of any material, corresponding respectively to the index of refraction and to the attenuation coefficient, are linked by the Kramers–Kronig relations.

Practical effects of finiteness

The finiteness of the speed of light has implications for various sciences and technologies. For some it creates challenges or limits: for example, c, being the upper limit of the speed with which signals can be sent, provides a theoretical upper limit for the operating speed of microprocessors.[61] For others it creates opportunities, for example to measure distances.

Distance measurement

The diameter of the moon is about one quarter of that of Earth, and their distance is about thirty times the diameter of Earth. A beam of light starts from the Earth and reaches the Moon in about a second and a quarter.
A beam of light is depicted travelling between the Earth and the Moon in the same time it takes light to scale the distance between them: 1.255 seconds at its mean orbital (surface to surface) distance. The relative sizes and separation of the Earth–Moon system are shown to scale.

Radar systems measure the distance to a target by the time it takes a radio-wave pulse to return to the radar antenna after being reflected by the target: the distance to the target is half the round-trip transit time multiplied by the speed of light. A Global Positioning System (GPS) receiver measures its distance to GPS satellites based on how long it takes for a radio signal to arrive from each satellite, and from these distances calculates the receiver's position. Because light travels about 300,000 kilometres (186,000 miles) in one second, these measurements of small fractions of a second must be very precise. The Lunar Laser Ranging Experiment, radar astronomy and the Deep Space Network determine distances to the Moon, planets and spacecraft, respectively, by measuring round-trip transit times.

Astronomy

The finite speed of light is important in astronomy. Due to the vast distances involved, it can take a very long time for light to travel from its source to Earth. For example, it has taken 13 billion (13×109) years for light to travel to Earth from the faraway galaxies viewed in the Hubble Ultra Deep Field images.[citation needed] Those photographs, taken today, capture images of the galaxies as they appeared 13 billion years ago, when the universe was less than a billion years old. The fact that farther-away objects appear younger (due to the finite speed of light) allows astronomers to infer the evolution of stars, of galaxies, and of the universe itself.

Astronomical distances are sometimes expressed in light-years, especially in popular science publications.[62] A light‑year is the distance light travels in one year, around 9461 billion kilometres, 5879 billion miles, or 0.3066 parsecs. Proxima Centauri, the closest star to Earth after the Sun, is around 4.2 light‑years away.[63]

A celestial object will exhibit apparent motion due to the motion of the observer and the finiteness of the speed of light. This effect is called stellar aberration. For an observer on Earth, it can be up to 20 arcseconds due to the Earth's motion, and is taken into account for precise astronomical observations.[citation needed] Conversely, if a celestial object itself is moving, it will have moved a certain amount in time that the light needed to reach Earth. The correction needed to obtain the true (current) position is known as Light-time correction.[citation needed]

History

Ancient, medieval and early modern speculation

Until the early modern period, it was not known whether light travelled instantaneously or at a finite speed. The first extant recorded examination of this subject was in ancient Greece. Empedocles maintained that light was something in motion, and therefore must take some time to travel. Aristotle argued, to the contrary, that "light is due to the presence of something, but it is not a movement".[64] Euclid and Ptolemy advanced the emission theory of vision, where light is emitted from the eye, thus enabling sight. Based on that theory, Heron of Alexandria argued that the speed of light must be infinite because distant objects such as stars appear immediately upon opening the eyes.

Early Islamic philosophers initially agreed with the Aristotelian view that light had no speed of travel. In 1021, Islamic physicist Alhazen (Ibn al-Haytham) published the Book of Optics, in which he used experiments related to the camera obscura to support the now accepted intromission theory of vision, in which light moves from an object into the eye.[65] This led Alhazen to propose that light must therefore have a finite speed,[64][66][67] and that the speed of light is variable, decreasing in denser bodies.[67][68] He argued that light is a "substantial matter", the propagation of which requires time "even if this is hidden to our senses".[69]

Also in the 11th century, Abū Rayhān al-Bīrūnī agreed that light has a finite speed, and observed that the speed of light is much faster than the speed of sound.[70] Roger Bacon argued that the speed of light in air was not infinite, using philosophical arguments backed by the writing of Alhazen and Aristotle.[71][72] In the 1270s, Witelo considered the possibility of light travelling at infinite speed in a vacuum, but slowing down in denser bodies.[73]

A comment on a verse in the Rigveda by the 14th century Indian scholar Sayana mentioned a speed of light equivalent to about 186,400 miles per second, which was apparently chosen so that light would encircle the Puranic universe in one day.[74][75] Subhash Kak proclaimed this "the most astonishing 'blind hit' in the history of science!"[76] In 1574, the Ottoman astronomer and physicist Taqi al-Din concluded that the speed of light is finite, correctly explained refraction as the result of light traveling more slowly in denser bodies, and suggested that it would take a long time for light from distant stars to reach the Earth.[77][78]

In the early 17th century, Johannes Kepler believed that the speed of light was infinite since empty space presents no obstacle to it. René Descartes argued that if the speed of light were finite, the Sun, Earth, and Moon would be noticeably out of alignment during a lunar eclipse. Since such misalignment had not been observed, Descartes concluded the speed of light was infinite. Descartes speculated that if the speed of light were found to be finite, his whole system of philosophy might be demolished.[64]

First measurement attempts

In 1629, Isaac Beeckman proposed an experiment in which a person would observe the flash of a cannon reflecting off a mirror about one mile (1.6 km) away. In 1638, Galileo Galilei proposed an experiment, with an apparent claim to having performed it some years earlier, to measure the speed of light by observing the delay between uncovering a lantern and its perception some distance away. He was unable to distinguish whether light travel was instaneous or not, but concluded that if it weren't, it must nevertheless be extraordinarily rapid.[79][80] Galileo's experiment was carried out by the Accademia del Cimento of Florence in 1667, with the lanterns separated by about one mile, but no delay was observed. Based on the modern value of the speed of light, the actual delay in this experiment would be about 11 microseconds. Robert Hooke explained the negative results as Galileo had by pointing out that such observations did not establish the infinite speed of light, but only that the speed must be very great.

Early astronomical techniques

Main article: Rømer's determination of the speed of light
A diagram of a planet's orbit around the Sun and of a moon's orbit around another planet. The shadow of the latter planet is shaded.
Rømer's observations of the occultations of Io from Earth

The first quantitative estimate of the speed of light was made in 1676 by Ole Christensen Rømer. He was one of a group of astronomers of the French Royal Academy of Sciences who were studying the motion of Jupiter's moons as a means of determining the longitude at a remote location.[Note 8][81][82] From the observation that the periods of Jupiter's innermost moon Io appeared to be shorter when the earth was approaching Jupiter than when receding from it, he concluded that light travels at a finite speed, and was able to estimate that would take light 22 minutes to cross the diameter of Earth's orbit. Christiaan Huygens combined this estimate with an estimate for the diameter of the Earth's orbit to obtain an estimate of speed of light of 220000 km/s, 26% lower than the actual value.[83] The same effect was subsequently observed by Rømer for a "spot" rotating with the surface of Jupiter. Later observations also showed the effect with the three other Galilean moons, where it was more difficult to observe, thus laying to rest some further objections that had been raised.

Isaac Newton also accepted the finite speed. In his 1704 book Opticks he gives a value of "seven or eight minutes" for the time taken for light to travel from the Sun to the Earth (the modern value is 8 minutes 19 seconds).[84]

A star from location 1 emits a light ray forming an angle θ with the horizontal, which hits the objective of a telescope. While the light travels down the telescope to its eyepiece, the telescope moves to the right by a distance vh/c, where h is the projection of the telescope's length on the propagation direction of the light ray. This way, the light can reach the eyepiece even if the telescope forms an angle φ < θ with the horizontal, making the star appear to be in a location 2, displaced to the right with respect to 1.
Aberration of light: light from location 1 will appear to be from location 2 for a moving telescope due to the finite speed of light.

Between 1725 and 1728, James Bradley, while searching for stellar parallax, observed the apparent motion of the star Gamma Draconis depending on the season of the year. He realized that the motion (about 39 arcseconds) could not be a parallax (it was in the wrong direction at any given time) and, after ruling out several other possible causes, produced the theory of the aberration of light,[85] a vector addition of the velocity of light arriving from the star and the velocity of the Earth around its orbit. The effect is that an observer on the Earth will see the light coming from a slightly different angle than the "true" value which, for a star in the sky, means a slightly different position. The effect is greatest near the orbital pole which, for the Earth, is close to γ Draconis. Bradley was able to predict the aberration for several other stars, and confirm his predictions by observation.[85] His observations on γ Draconis gave a ratio of the speed of light to the mean linear speed of the Earth's orbital motion: Bradley's figure was that light travelled 10,210 times faster than the Earth in its orbit (the modern figure is 10,066 times faster) or, equivalently, that it would take light 8 minutes 12 seconds to travel from the Sun to the Earth.[85]

Earth-bound techniques

See also: Fizeau–Foucault apparatus
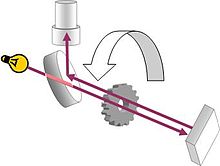
A light ray passes horizontally through a half-mirror and a rotating cog wheel, is reflected back by a mirror, passes through the cog wheel, and is reflected by the half-mirror into a monocular.
Diagram of the Fizeau apparatus

The first successful entirely earthbound measurement of the speed of light was carried out by Hippolyte Fizeau in 1849. Fizeau's experiment was conceptually similar to those proposed by Beeckman and Galileo. A beam of light was directed at a mirror 8 kilometres (5 mi) away. On the way from the source to the mirror, the beam passed through a rotating cog wheel. At a certain rate of rotation, the beam could pass through one gap on the way out and another on the way back, but at slightly higher or lower rates, the beam would strike a tooth and not pass through the wheel. Knowing the distance to the mirror, the number of teeth on the wheel, and the rate of rotation, the speed of light could be calculated. Fizeau reported the speed of light as 315000 km/s. Léon Foucault improved on Fizeau's method by replacing the cogwheel with a rotating mirror. Foucault's estimate, published in 1862, was 298000 km/s.[86]

In 1879, Albert Michelson performed a similar experiment at the US Naval Academy. He measured the speed of light in air to be 299864±51 kilometres per second, and estimated the speed of light in vacuum as 299,940 km/s, or 186,380 mi/s.[87]

In 1887, Michelson and Edward Morley performed an experiment to detect differences in the speed of light due to the Earth's motion through the luminiferous ether, at what is now Case Western Reserve University.[88] Its failure is generally considered to be the first strong evidence against the ether theory.

Cavity resonance

A box with three waves in it; there are one and a half wavelength of the top wave, one of the middle one, and a half of the bottom one.
Electromagnetic standing waves in a cavity.

During World War II, the development of the cavity resonance wavemeter for use in radar, together with precision timing methods, opened the way to laboratory-based measurements of the speed of light. In 1946, Louis Essen and A.C. Gordon-Smith used a microwave cavity of precisely known dimensions to establish the frequency for a variety of normal modes of microwaves. As the wavelength of the modes was known from the geometry of the cavity and from electromagnetic theory, knowledge of the associated frequencies enabled a calculation of the speed of light.[89][90]

The Essen–Gordon-Smith result, 299792±9 km/s, was substantially more precise than those found by optical techniques.[90] By 1950, repeated measurements by Essen established a result of 299792.5±3.0 km/s.[91]

Heterodyne laser measurements

In the top diagram, a lamp shines light onto two mirrors placed symmetrically, and the waves in reflections are in phase and sum up; in the bottom diagram, the right mirror is farther away from the lamp than the left mirror by one half-wavelength, so the waves in the reflections are out of phase and cancel out.
An idealized interferometric determination of wavelength obtained by looking at interference fringes between two coherent beams recombined after travelling different distances. Top: Constructive interference (in phase); If the difference in path length is a multiple of a wavelength, the recombined beams support one another and reconstitute the original beam. Bottom: Destructive interference (out of phase); If the two paths differ by half a wavelength, the recombined beams are out of phase and cancel each other. The bottom panel in the figure suggests the path length has been increased by half a wavelength by moving the right-hand point of reflection further out.

An alternative to the cavity resonator method to find the wavelength for determining the speed of light is to use a form of interferometer, indicated schematically in the figure.[92] A coherent light beam with a known frequency (f), as from a laser, is split to follow two paths and then recombined. By carefully changing the path length and observing the interference pattern, the wavelength of the light (λ) can be determined, which is related to the speed of light by the equation c = λf.

The main difficulty in measuring c through interferometry is to measure the frequency of light in or near the optical region; such frequencies are too high to be measured with conventional methods. This was first overcome by a group at the US National Institute of Standards and Technology (NIST) laboratories in Boulder, Colorado, in 1972.[93] By a series of photodiodes and specially constructed metal–insulator–metal diodes, they succeeded in linking the frequency of a methane-stabilized infrared laser to the frequency of the caesium transition used in atomic clocks (nearly 10,000 times lower, in the microwave region).[94] Their results for the frequency and wavelength of the infrared laser, and the resulting value for c, were:

f = 88.376181627±0.000000050 THz;
λ = 3.392231376±0.000000012 μm;
c = 299792456.2±1.1 m/s;

nearly a hundred times more precise than previous measurements of the speed of light.[93][94]

Redefinition of the metre

See also: Metre

The 1972 measurement of the speed of light, with a relative uncertainty of 4×10−9, was not only a feat of experimental precision, but also revealed a limiting factor to how precisely the speed of light could be measured by any technique: almost all the remaining uncertainty in the value of the speed of light was due to uncertainty in the length of the metre.[93][94][95] Since 1960, the metre had been defined as a given number of wavelengths of the light of one of the spectral lines of a krypton lamp,[Note 9] but it turned out that the chosen spectral line was not perfectly symmetrical.[94] This made its wavelength, and hence the length of the metre, uncertain, because the definition did not specify what point on the line profile (e.g., its maximum-intensity point or its centre of gravity) it referred to.[Note 10] By analogy with a metal measuring rod, it was as if the rod were slightly fuzzy at each end—although comparable fuzziness at the ends of a one-metre rod would be apparent only at the atomic scale.

To get round this problem, in 1975, the 15th Conférence Générale des Poids et Mesures (CGPM) recommended using 299792458 metres per second for "the speed of propagation of electromagnetic waves in vacuum".[95] Based on this recommendation, the 17th CGPM in 1983 redefined the metre as "the length of the path travelled by light in vacuum during a time interval of 1⁄299792458 of a second".[97]

The effect of this definition gives the speed of light the exact value 299792458 m/s, which is nearly the same as the value 299792456.2±1.1 m/s obtained in the 1972 experiment. The CGPM chose this value to minimise any change in the length of the metre.[98][99] As a result, in the SI system of units the speed of light is now a defined constant[14] and no longer something to be measured.[94] Improved experimental techniques do not affect the value of the speed of light in SI units, but do result in a more precise realisation of the SI metre.[100][101]

Modern astronomical measurements

As described above, an important consideration in measuring the speed of light with high accuracy is using a precise standard of length. The SI unit of length is determined by c through the 1983 definition of the metre. Therefore, to measure the speed of light, one must use a standard of length that is not based on the SI metre and that is defined independently of c.

The astronomical unit is one such standard. It is approximately equal to the average distance between the Earth and the Sun.[Note 11] The "light time per unit distance"—the inverse of c, expressed in seconds per astronomical unit—can be measured by comparing the time taken for radio signals to reach different spacecraft in the Solar System, with their position calculated from the gravitational effects of the Sun and various planets. By combining many such measurements, a best fit value for the light time per unit distance is obtained. As of 2009, the best estimate, as approved by the International Astronomical Union (IAU), is:[103][104][105]

light time per unit distance: 499.004783836(10) s
c = 0.00200398880410(4) AU/s = 173.144632674(3) AU/d

The relative uncertainty in these measurements is 0.02 parts per billion (0.02×10−9), equivalent to the uncertainty in Earth-based measurements of length by interferometry.[106][107]

Laboratory demonstration

With modern oscilloscopes having time resolutions of less than one nanosecond, the speed of light can be directly measured by timing the delay of a light pulse from a laser or an LED reflected from a mirror, although this method is less precise than either the cavity resonator or the interferometric methods. This technique is used as a laboratory experiment in college physics classes.[108][109][110]

See also

Notes

  1. ^ The speed of light can also be expressed exactly in imperial units and US units, based on an inch of exactly 2.54 cm, as 186,282 miles, 698 yards, 2 feet, and 5+21⁄127 inches per second.[11]
  2. ^ However, the frequency of light can depend on the motion of the source relative to the observer (see Doppler effect).
  3. ^ Strictly speaking, it is only possible to experimentally verify that the two-way speed of light (for example from a source to a mirror and back again) is frame-independent, since it is impossible to measure the one-way speed of light (for example from a source to a distant detector) without some convention as to how clocks at the source and detector should be synchronized. However, by adopting Einstein synchronization for the clocks, the one-way speed of light becomes equal to the two way speed of light by definition.
  4. ^ Whereas moving objects will be measured to have shrunk along the line of relative motion, they will be seen as being rotated. This effect, known as Terrell rotation, is due to the different times that light from different parts of the object takes to reach the observer.[25][26]
  5. ^ See Relativity of simultaneity.
  6. ^ It is thought that the Scharnhorst effect does allow signals to travel slightly faster than c, but the special conditions in which this effect can occur prevent one from using this effect to violate causality.[35]
  7. ^ See Tachyonic antitelephone for an example.
  8. ^ Besides Rømer, the group included Giovanni Domenico Cassini and Jean Picard.
  9. ^ From 1960 to 1983, the metre was defined as "the length equal to 1,650,763.73 wavelengths in vacuum of the radiation corresponding to the transition between the levels 2p10 and 5d5 of the krypton-86 atom."[96]
  10. ^ The value of 299792456.2±1.1 m/s quoted above assumes that the definition of the metre is to be applied to the centre of gravity of the krypton line. The NIST group reported that using the maximum-intensity point of the line instead, the result would be 299792458.7±1.1 m/s.
  11. ^ The astronomical unit is defined the radius of an unperturbed circular Newtonian orbit about the Sun of a particle having infinitesimal mass, moving with a angular frequency of 0.01720209895 radians (approximately 1⁄365.256898 of a revolution) per day.[102] It has the advantage that the product of the gravitational constant multiplied by the solar mass has a fixed, exact value in cubic astronomical units per day squared.

References

Citations

  1. ^ a b c The International System of Units (PDF) (9th ed.), International Bureau of Weights and Measures, Dec 2022, p. 112, ISBN 978-92-822-2272-0
  2. ^ a b Penrose, R (2004). The Road to Reality: A Complete Guide to the Laws of the Universe. Vintage Books. pp. 410–1. ISBN 9780679776314. ... the most accurate standard for the metre is conveniently defined so that there are exactly 299,792,458 of them to the distance travelled by light in a standard second, giving a value for the metre that very accurately matches the now inadequately precise standard metre rule in Paris.
  3. ^ Uzan, J-P; Leclercq, B (2008). The Natural Laws of the Universe: Understanding Fundamental Constants. Springer. pp. 43–4. ISBN 0387734546.
  4. ^ Duke, PJ (2000). "Radiation from moving electrons". Synchrotron Radiation: Production and Properties. Oxford University Press. p. 53. ISBN 0198517580.
  5. ^ Schwinger, JS (2002) [1986]. "Gravitational waves". Einstein's Legacy: The Unity of Space and Time (Reprint ed.). Courier Dover. p. 223. ISBN 0486419746. {{cite book}}: External link in |chapterurl= (help); Unknown parameter |chapterurl= ignored (|chapter-url= suggested) (help)
  6. ^ Ni, W-T (2005). "Empirical foundation of the relativistic gravity" (PDF). International Journal of Modern Physics D. 14: 901–21. doi:10.1142/S0218271805007139.
  7. ^ Greene, G (2003). The Elegant Universe. W. W. Norton. pp. 55–6. ISBN 0393058581.
  8. ^ Davies, PCW (1979). The Forces of Nature. Cambridge University Press. pp. 127–8. ISBN 052122523X.
  9. ^ a b Taylor, EF; Wheeler, JA (1992). Spacetime Physics. W. H. Freeman. pp. 74–5. ISBN 0716723271.
  10. ^ Kirk, AG (2006). "Free-space optical interconnects". Optical Interconnects: The silicon approach. Birkhäuser. p. 343. ISBN 3540289100. {{cite book}}: External link in |chapterurl= (help); Unknown parameter |chapterurl= ignored (|chapter-url= suggested) (help); Unknown parameter |editors= ignored (|editor= suggested) (help)
    Hall, SG; Hall, GW; McCall, JA (2000). High Speed Digital System Design: A Handbook of Interconnect Theory and Design Practices. Wiley. p. 1. ISBN 0471360902.
    Gad, E; Nakla, M; Achar, R (2008). "Model-order reduction of high-speed interconnects using integrated congruence transform". Model Order Reduction. Springer. p. 362. ISBN 3540788409. {{cite book}}: External link in |chapterurl= (help); Unknown parameter |chapterurl= ignored (|chapter-url= suggested) (help); Unknown parameter |editors= ignored (|editor= suggested) (help)CS1 maint: extra punctuation (link)
  11. ^ Savard, J. "From Gold Coins to Cadmium Light". John Savard's Home Page. Retrieved 2009-11-14. {{cite web}}: External link in |work= (help) (Archived version 2009-11-14.)
  12. ^ Sydenham, PH (2003). "Measurement of length". In Boyes, W (ed.). Instrumentation Reference Book (3rd ed.). Butterworth–Heinemann. p. 56. ISBN 0750671238. ... if the speed of light is defined as a fixed number then, in principle, the time standard will serve as the length standard ... {{cite book}}: External link in |chapterurl= (help); Unknown parameter |chapterurl= ignored (|chapter-url= suggested) (help)
  13. ^ "Fundamental Physical Constants: Speed of Light in Vacuum". NIST. Retrieved 2009-08-21.
  14. ^ a b Jespersen, J; Fitz-Randolph, J; Robb, J (1999). From Sundials to Atomic Clocks: Understanding Time and Frequency (Reprint of National Bureau of Standards 1977, 2nd ed.). Courier Dover. p. 280. ISBN 0486409139.
  15. ^ Gibbs, P (2004) [1997]. "Why is c the symbol for the speed of light?". Usenet Physics FAQ. University of California, Riverside. Retrieved 2009-11-16. Archived version 2009-11-17
  16. ^ Mendelson, KS (2006). "The story of c" (subscription required). American Journal of Physics. 74 (11): 995–97. doi:10.1119/1.2238887.
  17. ^ See for example:
  18. ^ Lawrie, ID (2002). "Appendix C: Natural units". A Unified Grand Tour of Theoretical Physics (2nd ed.). CRC Press. p. 540. ISBN 0750306041. {{cite book}}: External link in |chapterurl= (help); Unknown parameter |chapterurl= ignored (|chapter-url= suggested) (help)
  19. ^ a b Hsu, L (2006). "Appendix A: Systems of units and the development of relativity theories". A Broader View of Relativity: General Implications of Lorentz and Poincaré Invariance (2nd ed.). World Scientific. pp. 427–8. ISBN 9812566511. {{cite book}}: External link in |chapterurl= (help); Unknown parameter |chapterurl= ignored (|chapter-url= suggested) (help) Cite error: The named reference "Hsu" was defined multiple times with different content (see the help page).
  20. ^ Einstein, A (1905). "Zur Elektrodynamik bewegter Körper" (PDF). Annalen der Physik (in German). 17: 890–921. English translation: Perrett, W; Jeffery, GB (tr.); Walker, J (ed.). "On the Electrodynamics of Moving Bodies". Fourmilab. Retrieved 2009-11-27. {{cite web}}: |first3= has generic name (help)
  21. ^ a b Zhang, YZ (1997). Special Relativity and Its Experimental Foundations. Advanced Series on Theoretical Physical Science. Vol. 4. World Scientific. pp. 172–3. ISBN 9810227493.
  22. ^ d'Inverno, R (1992). Introducing Einstein's Relativity. Oxford University Press. pp. 19–20. ISBN 0198596863.
  23. ^ Sriranjan, B (2004). "Postulates of the special theory of relativity and their consequences". The Special Theory to Relativity. PHI Learning. pp. 20 ff. ISBN 812031963X. {{cite book}}: External link in |chapterurl= (help); Unknown parameter |chapterurl= ignored (|chapter-url= suggested) (help)
  24. ^ Roberts, T; Schleif, S; Dlugosz, JM (ed.) (2007). "What is the experimental basis of Special Relativity?". Usenet Physics FAQ. University of California, Riverside. Retrieved 2009-11-27. {{cite web}}: |first3= has generic name (help)
  25. ^ Terrell, J (1959). "Invisibility of the Lorentz Contraction". Physical Review. 116: 1041–5. doi:10.1103/PhysRev.116.1041.
  26. ^ Penrose, R (1959). "The Apparent Shape of a Relativistically Moving Sphere". Proceedings of the Cambridge Philosophical Society. 55: 137–9. doi:10.1017/S0305004100033776.
  27. ^ Hartle, JB (2003). Gravity: An Introduction to Einstein's General Relativity. Addison-Wesley. pp. 52–9. ISBN 9810227493.
  28. ^ Hartle, JB (2003). Gravity: An Introduction to Einstein's General Relativity. Addison-Wesley. p. 332. ISBN 9810227493.
  29. ^ a b Gibbs, P (1997) [1996]. Carlip, S (ed.). "Is The Speed of Light Constant?". Usenet Physics FAQ. University of California, Riverside. Retrieved 2009-11-26. archived version 2009-11-17
  30. ^ Ellis, GFR; Uzan, J-P (2005). "'c' is the speed of light, isn't it?". American Journal of Physics. 73: 240–7. doi:10.1119/1.1819929. arXiv:gr-qc/0305099. The possibility that the fundamental constants may vary during the evolution of the universe offers an exceptional window onto higher dimensional theories and is probably linked with the nature of the dark energy that makes the universe accelerate today.
  31. ^ An overview can be found in the dissertation of Mota, DF (2006). "Variations of the fine structure constant in space and time". arXiv:astro-ph/0401631. {{cite arXiv}}: |class= ignored (help)
  32. ^ Uzan, J-P (2003). "The fundamental constants and their variation: observational status and theoretical motivations". Reviews of Modern Physics. 74: 403. doi:10.1103/RevModPhys.75.403. arXiv:hep-ph/0205340.
  33. ^ Farrell, DJ; Dunning-Davies, J (2007). "The constancy, or otherwise, of the speed of light". In Ross, LV (ed.). New Research on Astrophysics, Neutron Stars and Galaxy Clusters. Nova Publishers. pp. 71ff. ISBN 1600211100. {{cite book}}: External link in |chapterurl= (help); Unknown parameter |chapterurl= ignored (|chapter-url= suggested) (help)
  34. ^ Amelino-Camelia, G (2008). "Quantum Gravity Phenomenology". arXiv:0806.0339 [gr-qc].
  35. ^ Liberati, S; Sonego, M; Visser (2002). "Faster-than-c signals, special relativity, and causality". Annals of Physics. 298: 167–85. doi:10.1006/aphy.2002.6233. arXiv:gr-qc/0107091.
  36. ^ Tolman, RC (2009) [1917]. "Velocities greater than that of light". The Theory of the Relativity of Motion (Reprint ed.). BiblioLife. p. 54. ISBN 978-1-103-17233-7.
  37. ^ Wertheim, M (2007). "The Shadow Goes". The New York Times. Retrieved 2009-08-21.
  38. ^ a b c Gibbs, P (1997). "Is Faster-Than-Light Travel or Communication Possible?". Usenet Physics FAQ. University of California, Riverside. Retrieved 2008-08-20. Archived version 2009-11-17
  39. ^ Sakurai, JJ (1994). T, S (ed.). Modern Quantum Mechanics (Revised ed.). Addison-Wesley. pp. 231–2. ISBN 0-201-53929-2.
  40. ^ Muga, JG; Mayato, RS; Egusquiza, IL, eds (2007). Time in Quantum Mechanics. Springer. p. 48. ISBN 3540734724. {{cite book}}: |first3= has generic name (help)CS1 maint: multiple names: authors list (link)
  41. ^ Hernández-Figueroa, HE; Zamboni-Rached, M; Recami, E (2007). Localized Waves. Wiley Interscience. p. 26. ISBN 0470108851.
  42. ^ Wynne, K (2002). "Causality and the nature of information" (PDF). Optics Communications. 209: 84–100. doi:10.1016/S0030-4018(02)01638-3.
  43. ^ Rees, M (1966). "The Appearance of Relativistically Expanding Radio Sources". Nature. 211: 468. doi:10.1038/211468a0.
  44. ^ Chase, IP. "Apparent Superluminal Velocity of Galaxies". Usenet Physics FAQ. University of California, Riverside. Retrieved 2009-11-26.
  45. ^ Panofsky, W; Phillips, M (1962). Classical Electricity and Magnetism. Addison-Wesley. p. 182.
  46. ^ Schaefer, BE (1999). "Severe limits on variations of the speed of light with frequency". Physical Review Letters. 82: 4964–6. doi:10.1103/PhysRevLett.82.4964. arXiv:astro-ph/9810479.
  47. ^ Ellis, J; Mavromatos, DV; Sakharov, AS (2003). "Quantum-Gravity Analysis of Gamma-Ray Bursts using Wavelets". Astronomy & Astrophysics. 403: 409–24. doi:10.1051/0004-6361:20030263. arXiv:astro-ph/0210124.
  48. ^ Füllekrug, M (2004). "Probing the Speed of Light with Radio Waves at Extremely Low Frequencies". Physical Review Letters. 93: 043901. doi:10.1103/PhysRevLett.93.043901.
  49. ^ a b Adelberger, E; Dvali, G; Gruzinov, A (2007). "Photon Mass Bound Destroyed by Vortices". Physical Review Letters. 98: 010402. doi:10.1103/PhysRevLett.98.010402. arXiv:hep-ph/0306245.
  50. ^ Sidharth, BG (2008). The Thermodynamic Universe. World Scientific. p. 134. ISBN 9812812342.
  51. ^ Amelino-Camelia, G (2009). "Astrophysics: Burst of support for relativity". Nature. 462: 291–292. doi:10.1038/462291a.
  52. ^ Feynman, RP (1963). "Chapter 31: The Origin of the Refractive Index". The Feynman Lectures on Physics Volume I. Addison-Wesley.
  53. ^ de Podesta, M (2002). Understanding the Properties of Matter. CRC Press. p. 131. ISBN 0415257883.
  54. ^ Hau, LV; Harris, SE; Dutton, Z; Behroozi, CH (1999). "Light speed reduction to 17 metres per second in an ultracold atomic gas" (PDF). Nature. 397: 594–8. doi:10.1038/17561.
  55. ^ Liu, C; Dutton, Z; Behroozi, CH; Hau, LV (2001). "Observation of coherent optical information storage in an atomic medium using halted light pulses" (PDF). Nature. 409 (6819): 490–3. doi:10.1038/35054017. PMID 11206540.
  56. ^ Bajcsy, M; Zibrov, AS; Lukin, MD (2003). "Stationary pulses of light in an atomic medium". Nature. 426 (6967): 638–41. doi:10.1038/nature02176. PMID 14668857.
  57. ^ Dumé, B (2003). "Switching light on and off". Physics World. Retrieved 2008-12-08.
  58. ^ Wang, LJ; Kuzmich, A; Dogario, A (2000). "Gain-assisted superluminal light propagation". Nature. 406 (406): 277. doi:10.1038/35018520. PMID 10917523.
  59. ^ Whitehouse, D (19 July 2000). "Beam Smashes Light Barrier". BBC News. Retrieved 2008-12-08.
  60. ^ Brunner, N; Scarani, V; Wegmüller, M; Legré, M; Gisin, N (2004). "Direct measurement of superluminal group velocity and signal velocity in an optical fiber". Physical Review Letters. 93 (20): 203902. doi:10.1103/PhysRevLett.93.203902.
  61. ^ B Parhami (1999). Introduction to parallel processing: algorithms and architectures. p. 5. ISBN [[Special:BookSources/9780306459702|<span dir="ltr">9780306459702]]. {{cite book}}: |author= has generic name (help); Check |isbn= value: invalid character (help); Check date values in: |year= (help); External link in |author= (help)CS1 maint: numeric names: authors list (link) CS1 maint: year (link)
  62. ^ "The IAU and astronomical units". International Astronomical Union. Retrieved 2009-10-27.
  63. ^ Further discussion can be found at "StarChild Question of the Month for March 2000". StarChild. NASA. 2000. Retrieved 2009-08-22.
  64. ^ a b c MacKay, RH; Oldford, RW (2000). "Scientific Method, Statistical Method and the Speed of Light". Statistical Science. 15 (3): 254–78. doi:10.1214/ss/1009212817.
  65. ^ Steffens, B (2007). "The Scholar of Cairo". Ibn al-Haytham: First Scientist. Morgan Reynolds. ISBN 1599350246. {{cite book}}: External link in |chapterurl= (help); Unknown parameter |chapterurl= ignored (|chapter-url= suggested) (help)
  66. ^ Hamarneh, S (1972). "Review: Hakim Mohammed Said, Ibn al-Haitham". Isis. 63 (1): 119. doi:10.1086/350861.
  67. ^ a b Lester, PM (2005). Visual Communication: Images With Messages. Thomson Wadsworth. pp. 10–11. ISBN 0534637205.
  68. ^ O'Connor, John J.; Robertson, Edmund F., "Abu Ali al-Hasan ibn al-Haytham", MacTutor History of Mathematics Archive, University of St Andrews, retrieved 2010-01-12
  69. ^ Lauginie, P (2005). "Measuring: Why? How? What?" (PDF). Proceedings of the 8th International History, Philosophy, Sociology & Science Teaching Conference. Retrieved 2008-07-18. {{cite conference}}: Unknown parameter |booktitle= ignored (|book-title= suggested) (help)
  70. ^ O'Connor, John J.; Robertson, Edmund F., "Abu Arrayhan Muhammad ibn Ahmad al-Biruni", MacTutor History of Mathematics Archive, University of St Andrews, retrieved 2010-01-12
  71. ^ Lindberg, DC (1996). Roger Bacon and the origins of Perspectiva in the Middle Ages: a critical edition and English translation of Bacon's Perspectiva, with introduction and notes. Oxford University Press. p. 143. ISBN 0198239920.
  72. ^ Lindberg, DC (1974). "Late Thirteenth-Century Synthesis in Optics". In Edward Grant (ed.). A source book in medieval science. Harvard University Press. p. 396. ISBN 9780674823600.
  73. ^ Marshall, P (1981). "Nicole Oresme on the Nature, Reflection, and Speed of Light". Isis. 72 (3): 357–74 [367–74]. doi:10.1086/352787.
  74. ^ Kak, SC (5 January 2001 [v3]). "The Speed of Light and Puranic Cosmology". arXiv:physics/9804020. {{cite arXiv}}: Check date values in: |date= (help); Unknown parameter |origdate= ignored (help); Unknown parameter |url= ignored (help) Originally published in Annals of the Bhandarkar Oriental Research Institute, 80: 113–23 (1999).
  75. ^ Kak, SC (1998). "Sayana's Astronomy" (PDF). Indian Journal of History of Science. 33: 31–6.
  76. ^ Kak, The Speed of Light and Puranic Cosmology, p. 12.
  77. ^ Topdemir, HG (1999). Takîyüddîn'in Optik Kitabi. Ankara: Ministry of Culture Press.
  78. ^ Topdemir, HG (30 June 2008). "Taqi al-Din ibn Ma'ruf and the Science of Optics: The Nature of Light and the Mechanism of Vision". MuslimHeritage.com. Retrieved 2010-01-16.)
  79. ^ Boyer, CB (1941). "Early Estimates of the Velocity of Light". Isis. 33 (1): 24. doi:10.1086/358523.
  80. ^ Galilei, G (1954) [1638]. Dialogues Concerning Two New Sciences. Crew, H; de Salvio A (trans.). Dover Publications. p. 43. ISBN 486-60099-8. {{cite book}}: Check |isbn= value: length (help)
  81. ^ Cohen, IB (1940). "Roemer and the first determination of the velocity of light (1676)". Isis. 31 (2): 327–79. doi:10.1086/347594.
  82. ^ Rømer, O (1676). "Touchant le mouvement de la lumiere trouvé par M. Rŏmer de l'Académie Royale des Sciences" (PDF). Journal des Sçavans (in French): 233–6.
    Although Rømer read a report on his work to the French Academy of Sciences in November 1676 (Cohen, 1940, p.346), he does not appear to have written the published account. An electronic copy of the latter (in French) and one of a 1677 English translation are available online.
  83. ^ Huygens, C (1690). Traitée de la Lumière (in French). Pierre van der Aa. pp. 8–9.
  84. ^ Newton, I (1704). "Prop. XI". Optiks. The text of Prop. XI is identical between the first (1704) and second (1719) editions.
  85. ^ a b c Bradley, J (1729), "Account of a new discoved Motion of the Fix'd Stars", Philosophical Transactions, 35: 637–60
  86. ^ Gibbs, P (1997). "How is the speed of light measured?". Usenet Physics FAQ. University of California, Riverside. Retrieved 2010-01-13.
  87. ^ Michelson, AA (1880). "Experimental Determination of the Velocity of Light Made at the U.S. Naval Academy, Annapolis". Washington: Nautical Almanac Office of the US Naval Observatory. Retrieved 2009-12-05. {{cite journal}}: Cite journal requires |journal= (help)
  88. ^ Michelson, AA; Morley, EW (1887). "On the Relative Motion of the Earth and the Luminiferous Ether" . American Journal of Science. 34: 333–345.
  89. ^ Essen, L (1947). "Velocity of Electromagnetic Waves". Nature. 159 (4044): 611–612. Bibcode:1947Natur.159..611E. doi:10.1038/159611a0.
  90. ^ a b Essen, L; Gordon-Smith, AC (1948). "The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator". Proceedings of the Royal Society of London A. 194 (1038): 348–361. Bibcode:1948RSPSA.194..348E. JSTOR 98293.
  91. ^ Essen, L (1950). "The Velocity of Propagation of Electromagnetic Waves Derived from the Resonant Frequencies of a Cylindrical Cavity Resonator". Proceedings of the Royal Society of London A. 204 (1077): 260–277. Bibcode:1950RSPSA.204..260E. JSTOR 98433.
  92. ^ A detailed discussion of the interferometer and its use for determining the speed of light can be found in Vaughan, JM (1989). The Fabry-Perot interferometer. CRC Press. p. 47, pp. 384–391. ISBN 0852741383.
  93. ^ a b c Evenson, KM (1972). "Speed of Light from Direct Frequency and Wavelength Measurements of the Methane-Stabilized Laser". Physical Review Letters. 29: 1346–9. doi:10.1103/PhysRevLett.29.1346. {{cite journal}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)
  94. ^ a b c d e Sullivan, DB. "Speed of Light From Direct Frequency and Wavelength Measurements" (PDF). NIST. p. 191–93. Retrieved 2009-08-22.
  95. ^ a b "Resolution 2 of the 15th CGPM", Conférence Générale des Poids et Mesures, BIPM, 1975, retrieved 2009-09-09
  96. ^ "Resolution 6 of the 11th CGPM", Conférence Générale des Poids et Mesures, BIPM, 1960, retrieved 2009-10-18
  97. ^ "Resolution 1 of the 17th CGPM". Conférence Générale des Poids et Mesures. BIPM. 1983. Retrieved 2009-08-23.
  98. ^ Taylor, EF; Wheeler, JA (1992). Spacetime Physics: Introduction to Special Relativity (2nd ed.). Macmillan. ISBN 0716723271.
  99. ^ Penzes, WB (2009). "Time Line for the Definition of the Meter". NIST. Retrieved 2010-01-11.
  100. ^ Adams, S (1997). Relativity: An Introduction to Space-Time Physics. CRC Press. p. 140. ISBN 0748406212. One peculiar consequence of this system of definitions is that any future refinement in our ability to measure c will not change the speed of light (which is a defined number), but will change the length of the meter!
  101. ^ Rindler, W (2006). Relativity: Special, General, and Cosmological (2nd ed.). Oxford University Press. p. 41. ISBN 0198567316. Note that [...] improvements in experimental accuracy will modify the meter relative to atomic wavelengths, but not the value of the speed of light!
  102. ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), p. 126, ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16.
  103. ^ Pitjeva, EV; Standish, EM (2009). "Proposals for the masses of the three largest asteroids, the Moon-Earth mass ratio and the Astronomical Unit". Celestial Mechanics and Dynamical Astronomy. 103 (4): 365–72. doi:10.1007/s10569-009-9203-8.
  104. ^ IAU Working Group on Numerical Standards for Fundamental Astronomy. "IAU WG on NSFA Current Best Estimates". US Naval Observatory. Retrieved 2009-09-25.
  105. ^ "The Final Session of the General Assembly" (PDF), Estrella d'Alva: The Morning Star, p. 1, 14 August 2009
  106. ^ UK National Physical Laboratory, Length (poster), retrieved 2009-10-28
  107. ^ International Bureau of Weights and Measures (2003), Mise en pratique 2003 – Iodine (λ ≈ 633 nm) (in French) {{citation}}: |access-date= requires |url= (help)
  108. ^ Cooke, J; McCartney, H; Wilf, B (1968). "Direct determination of the speed of light as a general physics laboratory experiment". American Journal of Physics. 36 (9): 847. doi:10.1119/1.1975166. {{cite journal}}: |first2= missing |last2= (help); Text "Martin" ignored (help)
  109. ^ Aoki, K; Mitsui, T (2008). "A small tabletop experiment for a direct measurement of the speed of light". American Journal of Physics. 76 (9): 812–15. doi:10.1119/1.2919743. arXiv:0705.3996.
  110. ^ James, MB; Ormond, RB; Stasch, AJ (1999). "Speed of light measurement for the myriad". American Journal of Physics. 67 (8): 681–14. doi:10.1119/1.19352.

Historical references

Modern references

Template:Link FA Template:Link FA Template:Link FA

Retrieved from "https://en.wikipedia.org/w/index.php?title=Speed_of_light&oldid=341449946"