Welcome to the mathematics section
of the Wikipedia reference desk.

Select a section:

WP:RD/MA

Want a faster answer?

Main page: Help searching Wikipedia

How can I get my question answered?

Select the section of the desk that best fits the general topic of your question (see the navigation column to the right).
Post your question to only one section, providing a short header that gives the topic of your question.
Type '~~~~' (that is, four tilde characters) at the end – this signs and dates your contribution so we know who wrote what and when.
Don't post personal contact information – it will be removed. Any answers will be provided here.
Please be as specific as possible, and include all relevant context – the usefulness of answers may depend on the context.
Note:
- We don't answer (and may remove) questions that require medical diagnosis or legal advice.
- We don't answer requests for opinions, predictions or debate.
- We don't do your homework for you, though we'll help you past the stuck point.
- We don't conduct original research or provide a free source of ideas, but we'll help you find information you need.

Ready? Ask a new question!

How do I answer a question?

Main page: Wikipedia:Reference desk/Guidelines

The best answers address the question directly, and back up facts with wikilinks and links to sources. Do not edit others' comments and do not give any medical or legal advice.

January 21

Riemannian geometry

How do you calculate a straight line in Riemannian geometry using a given coordinate system? For example, if I was using the surface of a sphere in spherical coordinates, what series of steps would I have to go through to find the equation of a great circle?

Will it tend to be feasible to solve symbolically, or would you have to do it numerically?

Alternately, what could I read to teach me to do that?

I know up to linear algebra and differential equations. — DanielLC 06:11, 21 January 2010 (UTC)[reply]

The closest analogue of a straight line on a curved manifold is a geodesic. If a string is made to stay on the surface then the geodesic is the one where you stretch the string. On a sphere like the world it is a great circle, planes fly along them. Dmcq (talk) 11:32, 21 January 2010 (UTC)[reply]

You need the geodesic curvature to be zero along the whole of the curve. Fly by Night (talk) 13:25, 21 January 2010 (UTC)[reply]

How do you find that using only the metric tensor? From what I managed to find, there isn't generally a closed-form solution. Is it simple to find a taylor series solution? — DanielLC 19:59, 22 January 2010 (UTC)[reply]

Even with simple figures you find integrals of square roots coming in, you might get a trig function but you're quite liable to get something much worse. what are you expecting really? Try expressing even the great circles of a sphere easily and that's as simple as they come. Dmcq (talk) 20:26, 22 January 2010 (UTC)[reply]

I'm just asking if you could find the taylor series. It seems like it would be simple enough. I doubt there's any difficulty in just finding the geodesic curvature. I can't imagine finding the change in geodesic curvature would be much harder. Keep doing that and you get the taylor series. I've only been able to find out how to get the geodesic curvature using an actual surface. — DanielLC 02:05, 23 January 2010 (UTC)[reply]

Taylor Series would not help very much. Taylor Series are local. You would need to prove that each and every term was zero. If you were to calculate the first 1,000 terms and found them all to be zero then that does not mean, for example, that the 2,001st term is zero. If you were able to prove that each and every term is zero then you would most probably be able to prove that the geodesic curvature is zero without resorting to Taylor Series at all. Fly by Night (talk) 19:44, 25 January 2010 (UTC)[reply]

Fractional chromatic number

What is the fractional chromatic number of the United States? --84.61.165.65 (talk) 17:21, 21 January 2010 (UTC)[reply]

Sounds like the Six degrees of separation, but it might also be generated by a new AI. It does help to just invest that extra minute or two making things clearer if you're going ask people to spend time on something. Dmcq (talk) 17:33, 21 January 2010 (UTC)[reply]

What is the chromatic number of the United States? --84.61.165.65 (talk) 17:42, 21 January 2010 (UTC)[reply]

The US isn't a graph. What do you mean? You mean the states as vertices with edges between those that border each other? Or the resident people as vertices with edges between those that know each other? Or what? --Tango (talk) 17:44, 21 January 2010 (UTC)[reply]

I mean the states as vertices with edges between those that border each other. --84.61.165.65 (talk) 17:58, 21 January 2010 (UTC)[reply]

Plus I guess he means Fractional coloring rather than the straight chromatic number but I've not come across fractional coloring before. Dmcq (talk) 18:02, 21 January 2010 (UTC)[reply]

Fractional chromatic number redirects to Fractional coloring, which does define the term. --Tango (talk) 18:09, 21 January 2010 (UTC)[reply]

4 is an upper bound on both numbers: File:Map of USA with state names.svg. That's hardly surprising, given that the graph is planar. — Emil J. 18:26, 21 January 2010 (UTC)[reply]

Why is the chromatic number of the United States not smaller than 4? --84.61.165.65 (talk) 18:43, 21 January 2010 (UTC)[reply]

West Virginia and the adjoining states are already not three-colourable. Algebraist 18:49, 21 January 2010 (UTC)[reply]

Well the fractional version is ≤7/2. ~~I don't really want to try 3-fold coloring by hand though. :)~~ Edit: Since the graph H with 1 point surrounded by 5 has χ_f(H) = 7/2, and the US map has H as a subgraph, the fractional chromatic number of the U.S. map is exactly 7/2. Rckrone (talk) 20:01, 21 January 2010 (UTC)[reply]

I want a proof of the fact that the fractional chromatic number of the U.S. map is not greater than 7/2. --84.61.165.65 (talk) 20:27, 21 January 2010 (UTC)[reply]

Try 2-fold coloring it. Rckrone (talk) 20:37, 21 January 2010 (UTC)[reply]

Expected value problem

I've been looking at some self-generated 2-dimensional probability problems, and have got stuck. I'm considering a kind of random walk, specifically the case of a particle initially being at a particular distance $d$ (≥1) from the origin, then moving by unit distance in a uniformly-distributed direction. If it is then distance $r$ from the origin, what is E[ $r$ ]? For $d=1$ the answer comes fairly readily to be 4/π via the pdf of $r$ , but for general $d$ I got totally lost, and for the particular case of $d=2$ the integration was beyond me. Numerical simulation showed that E[ $r$ ] always exceeds $d$ , with the ratio decreasing towards 1 as $d$ increases, but didn't help in getting a general result - is there one?→86.155.184.123 (talk) 19:11, 21 January 2010 (UTC)[reply]

According to Wolfram Alpha, the answer is

2{\frac {d+1}{\pi }}E\left({\frac {4d}{(d+1)^{2}}}\right)

, where E is the complete elliptic integral of the second kind, whatever that may be. Algebraist 19:33, 21 January 2010 (UTC)[reply]

Wolfram uses a different notation from our article; the result is

2{\frac {d+1}{\pi }}E\left({\frac {2{\sqrt {d}}}{d+1}}\right)

in our notation.

It may also be interesting to know that the answer is

d+{\frac {1}{4d}}+{\frac {1}{64d^{3}}}+O\left({\frac {1}{d^{5}}}\right)

for large d and

1+{\frac {d^{2}}{4}}+{\frac {d^{4}}{64}}+O(d^{6})

for small d. -- Meni Rosenfeld (talk) 19:54, 21 January 2010 (UTC)[reply]

can you explain turbo codes OR LDPC?

I don't really care which one, which proves that this isn't homework (and it's not) but could someone explain EITHER turbo codes or LDPC in a way I can actually understand? I'm having so much trouble following either articles... thanks! 84.153.235.239 (talk) 19:31, 21 January 2010 (UTC)[reply]

p.s. I don't mean the effect, the net outcome, but the math: how it's actually done. Thanks again.

Error detection and correction is a huge subject and it's hard to know where you want to start. If you haven't heard of Shannon's theorem then I'd suggest getting a book on the subject.--RDBury (talk) 00:12, 22 January 2010 (UTC)[reply]

Try this: you've got a set of M possible messages to be encoded into an n-dimensional codeword space. If you map each message to a single codepoint in n-dimensional codeword space, and transmit that message into your channel, you can perform error detection by finding the nearest message codepoint to the received codeword point. If the encoded message points are far enough from one another, you can decode to the correct original message even if the received codeword is quite far away from the transmitted codeword.

The problem then becomes a very simple one: how do you pack M points into n-dimensional space while maximizing the distances between those points, yet still retaining a simple, fast algorithm for finding the nearest codepoint given a codeword? All the different error-correcting codes are ways of addressing this single problem for a variety of different constraints, and metrics for what is considered to be "near".

Shannon's noisy-channel coding theorem establishes a best-case bound on what is possible, by considering a very general scenario; LDPC and Turbo codes are ingenious attempts at solving the problem above that can get very close to the Shannon limit, providing n is sufficiently large for any given M.

Understanding Shannon's coding theorem is the key to understanding. There is a really good treatment of the underlying reasoning here, which is not unduly mathematical, and, if I recall correctly, rather similar to the treatment used in Shannon's original paper. -- The Anome (talk) 08:24, 22 January 2010 (UTC)[reply]

Sorry, the above is ALMOST easy enough for me to understand, but you could you simplify exactly what "n-dimensional" codespace is? How am I supposed to visualize that? Thanks!! 82.113.121.203 (talk) 03:23, 23 January 2010 (UTC)[reply]

n-dimensional codespace is the set of n-tuples. For n=1, 2, or 3 it is visualized as line, plane or space. For n>3 it is not actually visualized, but the concepts of point and distance are used. Bo Jacoby (talk) 08:15, 23 January 2010 (UTC).[reply]

January 22

Weaker versions of Fermat's Last Theorem

Andrew Wiles proved that Fermat's Last Theorem is true, i.e. that for the equation $a^{n}+b^{n}=c^{n}$ , there are no solutions where a, b, c and n are all natural numbers and n is greater than 2. What if we weaken the preconditions? If we allow at least one of a, b, and c to be any positive real, then it is trivially true that $a^{n}+b^{n}=c^{n}$ has solutions, because it reduces to checking whether $(a^{n}+b^{n})^{1/n}$ is a positive real, and such a positive real always exists. But what if we say that a, b, and c have to be natural numbers, but n can be any positive real? What can we say about what solutions exist for what values of n? JIP | Talk 07:04, 22 January 2010 (UTC)[reply]

For all natural numbers (a, b, c) such that c > a and c > b and c < a + b there exists a real number n such that

a^{n}+b^{n}=c^{n}

. I've discovered a lovely little proof of this, but this edit window is too small to contain it. Dragons flight (talk) 08:04, 22 January 2010 (UTC)[reply]

Let me try: ⊿. --Stephan Schulz (talk) 08:25, 22 January 2010 (UTC)[reply]

:-) Nice actually you don't need c<a+b (for real numbers 0<a≤b<c or 0<c<a≤b there exists a unique real n; if 0<a≤c≤b no such real n exists). --pm a 09:49, 22 January 2010 (UTC)[reply]

6³+7³>8³ but 6⁴+7⁴<8⁴, so there is a solution with a=6, b=7, c=8, and n somewhere between 3 and 4.--RDBury (talk) 13:35, 22 January 2010 (UTC)[reply]

I don't have a proof but just thinking it through I'm sure there's an infinity of a solution for n: take e.g. the above and double all the numbers. The solution will be the same but you can also modify a, b and c to get a slightly different equation with a different solution. Rinse and repeat with ever bigger numbers. There should be

\aleph _{0}

equations with solutions and so

\aleph _{0}

values for n. But there are

\aleph _{1}

real numbers in any interval, so an n picked at random will not be a solution. I don't know if you can say anything about the values for n other than this. --JohnBlackburne^words_deeds 13:49, 22 January 2010 (UTC)[reply]

Strictly speaking there are at least

\aleph _{1}

real numbers in any interval. AndrewWTaylor (talk) 14:15, 22 January 2010 (UTC) [reply]

The homogeneity of the equation suggests an alternative proof to the one which (I assume) Dragons flight had in mind. Show that for any real u, v such that 0 < u < 1 and 0 < v < 1 there is a real w > 0 such that

u^{w}+v^{w}=1

. Then take u = a/c and v = b/c. Gandalf61 (talk) 14:31, 22 January 2010 (UTC)[reply]

If w = 0 then

u^{w}+v^{w}=2

. The limit as w→+∞ is 0. So by continuity there is a value of w between 0 and +∞ where the expression =1. There are only countably many choices for u and v so the number of possible values for w is countable. In particular Fermat's last theorem says w can't be an integer greater than 3. It probably wouldn't be hard to show the possible ws are dense in some interval though. So even though you can't have w=3 you could get w arbitrarily close to 3.--RDBury (talk) 18:04, 22 January 2010 (UTC)[reply]

A variation on these lines: for a given positive integer n it's not hard to find countably many solutions in positive integers x,y,z of the Diophantine equation x^1/n+y^1/n=z^1/n. But can we characterize all solutions? In particular, is it necessary that x,y,z are perfect n-th powers? --84.220.119.131 (talk) 22:58, 22 January 2010 (UTC)[reply]

Bounds

Let us assume that a(t) and b(t) are, over ]0,∞[, both real valued and infinitely differentiable functions of the variable t. Furthermore, let us assume that the function c(t) is defined by c(t) = a(t) / b(t). Now, let us assume that the limit of c(t) as t tends towards positive infinity is k, where k is a positive real number. What can we say about a(t) and b(t)? What can we say about anything? Fly by Night (talk) 18:42, 22 January 2010 (UTC)[reply]

What sort of things do you want to say? We can say, for example, that b is eventually nonzero (that's the only constraint on b alone, though) and that a and b are eventually of the same sign. Algebraist 18:48, 22 January 2010 (UTC)[reply]

I wanted something more substantial than that. If we have two non-zero integers, say a and b, then we can form the number a/b. The integers cross the integers form a quotient space, namely the rational numbers: we say that (a,b) is in the same class as (c,d) if and only if ad = bc. Is their some kind of classification of pair of functions given a limit of their quotient? Fly by Night (talk) 19:05, 22 January 2010 (UTC)[reply]

There might be two equivalence relations. Define A(b, k) the set of functions which have limit k when divided by b, define B(a, k) the set of functions which have limit k when multiplied by a. My guess is that for every k, for every triplett of functions b, x, y it is true that: x in A(b, k) and y in A(b, k) => B(x, k) = B(y, k). Then B(A(b, k), k) could be an equivalence class for b. Maybe k is also irrelevant, so we get the class "all functions with similar limit behaviour as b". I don't know if that is actually true, but it sounds interesting and superficially plausible. —Preceding unsigned comment added by 80.226.1.7 (talk) 15:45, 23 January 2010 (UTC)[reply]

Simplify by substituting t=1/x because an infinite t is more confusing than a zero x. Pick an arbitrary positive continuous function C(x) with C(0)=k. Pick an arbitrary positive continuous function B(x). Define A(x)=B(x)C(x). All you can say is that lim_x→0A(x)/B(x)=k. Bo Jacoby (talk) 22:25, 22 January 2010 (UTC).[reply]

January 23

Finding a surface on which integrals of multiple functions are 0

Given a set of N linearly independent functions $f_{n}(x,y)$ on some bounded simply-conected 2D surface $S$ , under what conditions does there exist another surface $s\subset S$ on which the integrals of all $f_{n}(x,y)$ are 0? $\forall n:\int _{s}f_{n}(x,y)dA=0$

$s$ does not need to be connected.

I wrote a simple program to find $s$ given $f_{n}(x,y)$ , and the results indicate that it is sufficient that all $f_{n}(x,y)$ are continuous functions that change sign somewhere on $S$ . I know this is not a necessary condition, but I am most interested in knowing if this condition is indeed sufficient. 83.134.167.153 (talk) 08:32, 23 January 2010 (UTC)[reply]

Not sure what you're up to but it sounds like you want to look at Orthogonal functions. Dmcq (talk) 15:57, 23 January 2010 (UTC)[reply]

I don't think just changing sign is sufficient. For example if f₁ is strictly greater than f₂, then it won't work. Rckrone (talk) 17:30, 23 January 2010 (UTC)[reply]

By the Lyapunov convexity theorem the set

\scriptstyle \{(\int _{E}f_{1},\dots ,\int _{E}f_{n})\;:\;E\subset S,\;\mathrm {measurable} \}

is a closed convex set in

\scriptstyle \mathbb {R} ^{n}

, and (in fact, as a consequence) the same holds if you also prescribe

\scriptstyle |E|=c

or

\scriptstyle |E|\geq c

for a given number c. Therefore, if you are ok with a measurable subset s of S instead of an open set s, you have the following necessary and sufficient condition: there exists such a measurable subset s, say with

\scriptstyle |s|\geq c

if and only if there are

n

measurable sets with

\scriptstyle |E_{i}|\geq c

such that some convex combination of the

n+1

vectors in

\scriptstyle \mathbb {R} ^{n},

\scriptstyle v_{0}:=(\int _{E_{0}}f_{1},\dots ,\int _{E_{0}}f_{n}),\dots ,v_{n}:=(\int _{E_{n}}f_{1},\dots ,\int _{E_{n}}f_{n})

vanishes. If you really need s to be a surface (that is, an open subset of S since S itself is a surface) then you need the analogous Lyapunov convexity theorem, that I think is still true and existing somewhere there out, especially if

\scriptstyle f_{1},\dots ,f_{n}

are continuous. pma. --84.220.118.69 (talk) 18:17, 24 January 2010 (UTC)[reply]

January 24

Query on an online document - subgroups of A5

Hi all,

I was just wondering if anyone could explain to me briefly the logic behind a part of this link:

http://docs.google.com/viewer?a=v&q=cache%3Aw82TetVc1DEJ%3Awww.rose-hulman.edu%2Fmathjournal%2Farchives%2F2009%2Fvol10-n1%2Fpaper4%2Fv10n1-4pd.pdf+subgroups+of+A5+order+20&hl=en&gl=uk&sig=AHIEtbSsrQJRFZfAaRS7cE25dmdwlG9dFg

On page 5 of 7, around 2 thirds of the way down the page, it says with regards to A5, 'If there were a subgroup H of order 15 or 20, letting A5 act on the coset space G/H would give a nontrivial homomorphism φ : A5 → S3 or φ : A5 → S4. The kernel of φ in either case would be a proper nontrivial normal subgroup of A5, hence no such H exists.'

Now, how do we know that the homomorphism would necessarily be nontrivial for indexes of 3 or 4, but not for index 5 or 6, say? I can't see where the argument falls down in the step between 3 and 4, other than the fact that we can actually find a group of order 12 in A5? I presume there's a nicer way to show where the argument falls apart, without having to actually exhibit the order-12 group. Why is it that the homom. would necessarily be non-trivial for |A5:H|=3,4 but not 5 or 6?

Many thanks,

Typeships17 (talk) 03:15, 24 January 2010 (UTC)[reply]

It's still nontrivial for 5, but then you just get a homomorphism into S₅, which can be (and is) injective. The problem is that S₃ and S₄ are smaller than A₅, so the homomorphism can't be injective, so the kernel can't be trivial. Since the homomorphism is necessarily nontrivial (because the action on the coset space is clearly transitive), the kernel can't be A₅ either, so it must be a proper nontrivial normal subgroup, which of course doesn't exist. Algebraist 03:21, 24 January 2010 (UTC)[reply]

In general this argument shows that a simple group G of order ~~less~~ more than n! can't have a subgroup of index n. Slightly more thought shows that this holds if G just has order ~~less~~ more than n!/2. Algebraist 03:24, 24 January 2010 (UTC)[reply]

You mean a simple group of order *greater* than n! can't have a subgroup of index n > 1. In fact, a non-alternating simple group with a subgroup of index n (n large enough) has order bounded above by n^(c*log(n)). By comparison, n! is larger than (n/e)^n. JackSchmidt (talk) 07:50, 24 January 2010 (UTC)[reply]

That's nice. Is the proof amenable to brief explanation? Algebraist 15:00, 24 January 2010 (UTC)[reply]

I don't know if the "full" result is easy to explain, but there are some improvements to n!/2 that probably make a lot of sense. They eventually lead to the simple estimate that G cannot have order more than 4^n, which is better than 4^( c * n log(n) ) = n!/2, but worse than 4^( c*log(n)*log(n) ) = n^(c*log(n)) that I mentioned. A result of (Bochert 1889) shows that not only can you divide by 2, you can divide by the larger ((n+1)/2)! instead. Burnside's book apparently has one of the earlier versions, where you divide by a few more primes than just 2. This is mentioned in the paper (Manning 1915) which divides by a whole lot of primes, and might actually make a significant asymptotic difference. Basically it comes from looking at how Sylow subgroups can act; Sylows are small, and group orders are the product of their Sylows. A more advanced version of this is in (Praeger & Saxl 1980) which again uses bounds on the Sylows, splitting the primes into cases like Manning did, but using more modern estimates. They give the 4^n version.

Bochert, Alfred (1889), "Ueber die Zahl der verschiedenen Werthe, die eine Function gegebener Buchstaben durch Vertauschung derselben erlangen kann", Mathematische Annalen, 33 (4): 584–590, doi:10.1007/BF01444035, ISSN 0025-5831, MR1510562
Manning, W. A. (1915), "On the order of primitive groups. II", Transactions of the American Mathematical Society, 16 (2): 139–147, doi:10.2307/1988714, ISSN 0002-9947, MR1501006
Praeger, Cheryl E.; Saxl, Jan (1980), "On the orders of primitive permutation groups", The Bulletin of the London Mathematical Society, 12 (4): 303–307, doi:10.1112/blms/12.4.303, ISSN 0024-6093, MR576980

I don't remember an easy textbook like treatment of it, but I think results along these lines are discussed in Dixon-Mortimer. I'd check if Burnside's version is interesting and accessible. Let me know if you find an interesting and readable account; "subgroups of simple groups are ridiculously small" is one of my favorite themes to get across. JackSchmidt (talk) 17:27, 24 January 2010 (UTC)[reply]

College question: What material do I need to have a firm grasp on?

I am entering a college algebra course (some people call it pre-calculus) in a few weeks and I would like to know what prior material (Alg 1 & 2) I need to have a firm grasp on in order to make a smooth transition and be successful. I have never been very good at math but I am tremendously hard working. A list of topics or any advice would greatly appreciated. Thank you. —Preceding unsigned comment added by 161.165.196.84 (talk) 04:46, 24 January 2010 (UTC)[reply]

I recently ranted about College Algebra on -- maybe it was the science refdesk? Anyway, here's my perspective, as someone who's taught the course several times.

College Algebra (at least at the institution where I taught it) does not really go very far beyond Algebra I & II; it just does the same material faster. There are a few little wrinkles sometimes introduced, but I think they're fairly worthless (stuff like Dirichlet's Law of Signs or something like that).

My typical student was a lot like you've described yourself — never had a lot of success in math classes but willing to work very hard. This couldn't help but endear the students to me; they were very likable.

But unfortunately they were working hard in the wrong way. They preferred to memorize for an hour rather than think for five minutes. The outcome was usually not all that good.

My advice is not to do it that way. Put some effort into figuring out what's going on. If you don't understand what's going on, getting to where you do should be your priority over memorizing the recipes. Once you understand them, the recipes are pretty much obvious; you no longer need to memorize them.

Now, I should say that I'm not necessarily advising you how to get the best grade here. In the long run, this approach should get you the best grades too, but if this is the last math class you ever intend to take, then it's possible it won't "kick in" in time. So take it for what it's worth.

But if you actually want to get something out of the class, beyond checking off a general-ed requirement, then my way is really the only way. --Trovatore (talk) 05:04, 24 January 2010 (UTC)[reply]

Thank you for the response. I prefer your method due to the fact that it should afford me the greatest degree off success in my future calculus classes. When you say to "think for 5 minutes" what exactly do you mean? Can you explain to me the "right" thought proccess when confronted with a problem? Again, thank you for the help. —Preceding unsigned comment added by 161.165.196.84 (talk) 06:28, 24 January 2010 (UTC)[reply]

Obviously, the thought processes vary from problem to problem. I would suggest going over a similar problem that someone else has solved (I'm sure your lecturer will go over some, make sure you take detailed notes if they aren't provided). You then need to make sure you really understand what they did and why. If you really understand why they solved that problem like that, then you will find it easy to adapt the method to your problem. It is important that you understand the underlying theory, as well as how to solve problems. Make sure you really understand the definitions (working out how the definition works in extreme or trivial situations helps with that) and the statements of any results. Understanding the proofs also helps but, unless they are liable to come up in the exam (check that), you don't need to be able to reproduce them (often that just involves memorising the clever trick that is used - there usually is one - and that isn't useful for anything other than reproducing that proof). --Tango (talk) 07:10, 24 January 2010 (UTC)[reply]

Expanding on what Tango said, there is no single "right way to think", which is what makes it fun. Except of course when you're not getting anywhere; in that case it's what makes it painful. Maybe the most important thing to remember is, if the way you're thinking about it doesn't seem to be leading anywhere, try something else — and don't give up. The problems they give you at this level are all solvable. Sooner or later you'll hit on something.

Then try to remember the clarifying insight for next time.

I don't know how helpful these remarks really are — learning to think is a lifelong endeavor, and it's not realistic that I can help you much at that in a few lines. My encouragement to you is simply to actually do it. Use whatever you've already learned about how your thinking process works, and build on that. It gets more effective the more you do it, and the more you do it in a specific arena. Unfortunately most students, at least in the US, have not been exposed much to the idea that thinking is something that's actually required or even useful in a math class; you need to break out of that mindset. Best wishes for success; it can really be done. --Trovatore (talk) 07:37, 24 January 2010 (UTC)[reply]

I really don't understand US maths education... You're doing a pre-calc course at college? In the UK, if you are going to learn calculus, you do so aged 16/17. --Tango (talk) 07:10, 24 January 2010 (UTC)[reply]

U.S. students definitely have the opprotunity to take higher math courses while still in HS, I just chose not to..... unfortunately, I am now making up for it in college. —Preceding unsigned comment added by 161.165.196.84 (talk) 07:34, 24 January 2010 (UTC)[reply]

I'd answer your question for advice another way. The pre-requisites for such a course are limited. The best thing you could do would be to start on the textbook for the course a little early, and then just try to stay a leap ahead of the instructor.Julzes (talk) 08:30, 24 January 2010 (UTC)[reply]

You are under the misconception that there is one, and only one right way to think mathematically. Mathematics subsumes infinitely many different ways of thinking, and in fact the sorts of ways of thinking in existence will never be known. If otherwise, at one point in time everything about mathematics would be known, and this is of course impossible. It is therefore extremely important to appreciate that you will have to invent new ways of thinking should you pursue mathematics furthur. In fact, whatever you choose to study in the future, you will have to discover your own answers; neither your lecturer, nor even the most intelligent person in the world (not that one exists) can give you an answer to everything.

In any case, given the level of mathematics you are studying at present, you are not expected to invent new ways of thinking; ways unknown to all professional mathematicians. Nonetheless, it does help to develop your own ways of thinking; only you know those ways of thinking that result in maximal productivity for you. As a specific example, I would note that even after many years of experience in mathematical thinking, I occassionally find that I am thinking "too hard"; by this I imply thinking in a manner which gives one many original intuitions useful elsewhere but not effective in the context of the idea he/she is investigating. Thus, the best piece of advice I can offer you with regards to mathematical thinking is: "Think simply but abstractly" (you will learn the intended meaning of this "phrase" with time).

On another note, there are many ways in which you can "master" your precalculus course. Firstly, it is always useful to at least attempt to solve worked examples given in your book before (thoroughly) examining their solutions. This way, even if your attempts at the solutions result in failure, you will have some idea about the worked example making it easier to comprehend later on. Secondly, do not work too hard; if you are confident that you have a firm grasp of the material given in one chapter (that is, that you can solve a variety of textbook exercises without necessarily being able to solve them all), move on to the next chapter. Then, if time permits, you can return to solve any remaining exercises in previous chapters before the "final exam". By maintaining your workload at a minimum, you will remain interested in the course, and this is perhaps the most important factor in achieving good grades.

Lastly, specifically in response to your question, you should be comfortable around solving basic algebraic equations, factoring low degree polynomials, and perhaps, if possible, visualizing the graphs of basic polynomials. It is also useful to be familiar with trigonometry (trigonometric functions), but that very much depends on the content of your course. To summarize, do not be concerned if you cannot stick exactly to my advice; with time you will appreciate different ways of learning, and the advice I have given you now will become clear. Hope this helps. --PS T 12:38, 24 January 2010 (UTC)[reply]

A big thank you to all who replied!!!! your information is as helpful as it is inspirational. Finally, does anyone know of any good online resources (preferably FREE) that provide math instruction and/ or tests to keep the skills I have aquried fresh? Thanks again! —Preceding unsigned comment added by 161.165.196.84 (talk) 11:53, 26 January 2010 (UTC)[reply]

Factoring Polynomials

Is there a general method for substituting a polynomial (in one variable) into another so as to get a factorable result? In particular, I'm interested in whether the assumption of Schinzel's hypothesis H allows the claim that for any p the ratio of the largest to smallest prime factors of n^p+1 may be made arbitrarily close to 1. For p=2 and p=3, it's not difficult to get a desired factorization into irreducible polynomials (which can be prime, by the hypothesis). Whether something of the same kind can be done with larger p is what I'm after specifically, but of course I'd like to know the general answer if there is one. I'm not quite sure where to look it up.Julzes (talk) 04:55, 24 January 2010 (UTC)[reply]

Just in the simplest case after the ones mentioned, I guess I'd like quartic Q(x) such that P(Q(x)), P(x)=x^4-x^3+x^2-x+1, factors into four quartics.Julzes (talk) 05:02, 24 January 2010 (UTC)[reply]

Actually, Q wouldn't need to be quartic, and I wouldn't generally expect Q to have the same or a lower degree than P. The only thing needed is to get the same number of factors as the degree of P and for the leading terms--coefficient and degree--of the factors to be equal.Julzes (talk) 08:46, 24 January 2010 (UTC)[reply]

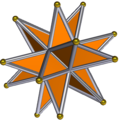
Complex icosidodecahedrons

Are these polyhedrons?

Small complex icosidodecahedron (Cid)
Great complex icosidodecahedron (Gacid)

4 T C 05:42, 24 January 2010 (UTC)[reply]

Yes. The clue is in the name - if it ends with "hedron" then it is a polyhedron (you don't get monohedrons - I suppose it would be another name for a solid polygon, but you never hear them called that). A polyhedron is a 3D shape made up of lots of flat faces (poly=many, hedron=faces). --Tango (talk) 07:14, 24 January 2010 (UTC)[reply]

Wouldn't a solid polygon be a dihedron as it has a top face and a bottom face? ;-) But anyway, since I made the articles from Mathworld, I still don't get where the faces are in these polyhedra. 4 T C 07:23, 24 January 2010 (UTC)[reply]

Yes, it could be a dihedron too. It depends on your exact definition - dealing with degenerate cases always tests just how good your definition is! --Tango (talk) 08:04, 24 January 2010 (UTC)[reply]

The first one just looks like an ordinary icosahedron to me; I don't see where the "dodeca" part comes in. --Trovatore (talk) 07:28, 24 January 2010 (UTC)[reply]

After some checking on MathWorld, it seems like the first one is a compound of an icosahedron and a great dodecahedron. That could be where the "dodeca" part comes in. 4 T C 07:37, 24 January 2010 (UTC)[reply]

I don't see a dodecahedron there, do you? Of course it's the dual of the icosahedron, so I suppose you can visualize a dodecahedron connecting the centers of the faces, but that's a bit strained — there's no obvious dodecahedron in the pic. --Trovatore (talk) 07:43, 24 January 2010 (UTC)[reply]

A big problem, yes. Actually, I meant great dodecahedron not a Platonic dodecahedron, but still we have the same problem: you can only see the icosahedron. Maybe someone could edit the picture to make this clearer. 4 T C 07:51, 24 January 2010 (UTC)[reply]

And in case you were wondering, I don't see a dodecahedron either. 4 T C 07:52, 24 January 2010 (UTC)[reply]

The shape shown in the picture is just an icosahedron. Presumably, if one could examine the actual 3-D model, then one would be able to see the more complex polyhedron with the dodecahedron inside. The picture needs clarification. Dbfirs 07:57, 24 January 2010 (UTC)[reply]

(undent) Or perhaps doing some rerendering. Actually, what really would help is to draw the icosahedron in wireframe, thus exposing the (solid) great dodecahedron inside. 4 T C 08:00, 24 January 2010 (UTC)[reply]

And the problem holds for the second one too. It's supposed to be a compound of a great icosahedron and a small stellated dodecahedron, but the picture is just a small stellated dodecahedron. The "wireframe solution" should also work here. 4 T C 08:02, 24 January 2010 (UTC)[reply]

Oops, no it doesn't. The "wireframe solution" would give the same problem in reverse - you would now see the other polyhedron in the compound, and just that. Has anyone got any ideas to resolve these issues? 4 T C 08:04, 24 January 2010 (UTC)[reply]

Something seems very sinister about polyhedra with coincident edges and vertices. Can they really be considered polyhedra after all? 4 T C 08:05, 24 January 2010 (UTC)[reply]

They're definitely not what I've ever thought of as polyhedra. The polyhedron page laments that there's no clear definition. I think I would at least require a polyhedron to be a compact C⁰ 2-manifold. I was going to add "injectively immersed in 3-space" but I suppose a triangulation of the Klein bottle ought to count as a polyhedron. --Trovatore (talk) 08:11, 24 January 2010 (UTC)[reply]

Could you please explain what a "compact C⁰ 2-manifold" is? I don't know much about manifolds... 4 T C 08:12, 24 January 2010 (UTC)[reply]

It means that at every point, locally, it has to look like Euclidean 2-space. So for example having three faces joining at the same edge is ruled out, because any neighborhood of a point on the edge would have a flap coming off it. --Trovatore (talk) 08:15, 24 January 2010 (UTC)[reply]

Incidentally, how can a manifold not be C⁰? Doesn't C⁰ just mean it is a topological space? --Tango (talk) 08:24, 24 January 2010 (UTC)[reply]

Right. The point of specifying C⁰ is to clarify that I'm not interested in the differential structure. --Trovatore (talk) 08:26, 24 January 2010 (UTC)[reply]

These two polyhedroids (since you don't think they're polyhedra anymore), have four faces at an edge - are they still compact C⁰ 2-manifolds? 4 T C 08:31, 24 January 2010 (UTC)[reply]

No, unless I'm missing something. --Trovatore (talk) 08:42, 24 January 2010 (UTC)[reply]

(undent) Thought so, but can't figure out why. 4 T C 08:44, 24 January 2010 (UTC)[reply]

No. Basically, you should be able to smoothly deform a polyhedron into a sphere (or, I suppose, a torus, Klein bottle, etc., but normally it's a sphere). You need to be able to deform in so, at any given point, it is nice and flat around it. There is no way of making a point where more than two faces meet flat. --Tango (talk) 08:49, 24 January 2010 (UTC)[reply]

OK, thanks for the great explanation. I see now - such "polyhedroids" have different Euler characteristics depend on how you consider the edges. 4 T C 09:06, 24 January 2010 (UTC)[reply]

The edges and vertices are fine. It's the faces that trouble me - I've never seen a polyhedron where the faces intersect each other, other than at an edge. I would consider the intersection of two faces to be an edge, by definition, really. Your articles describe them as "generalised polyhedra", which seems reasonable to me (I haven't come across the term before, but it makes sense). An article, generalised polyhedron, would be good, though. It seems that the definition of a polyhedron is generalised by allowing more than two faces to meet at an edge and allowing faces the intersect away from edges. --Tango (talk) 08:20, 24 January 2010 (UTC)[reply]

Then take a look at the dodecadodecahedron - some points and lines where the faces intersect are not true vertices and edges. 4 T C 08:28, 24 January 2010 (UTC)[reply]

Oh, yes, there are some edges meeting each other away from vertices, as well. I haven't noticed that. --Tango (talk) 08:49, 24 January 2010 (UTC)[reply]

How about rendering the outer polyhedron with 50% transparency? --Tango (talk) 08:20, 24 January 2010 (UTC)[reply]

Now there's a great idea! How about, then, chopping up the faces of the outer polyhedron until you can only see thin rectangles running along the edges? 4 T C 08:28, 24 January 2010 (UTC)[reply]

Most 3D graphics programs can do transparency themselves, the faces would just look slightly see-through. --Tango (talk) 08:49, 24 January 2010 (UTC)[reply]

(undent) But apart from these sticky issues, there are still more: how do you define the vertex figure for such a polyhedron? The Euler characteristic shows that they're compounds - one element in both of them has chi = -6 and the other has chi = 2. You can figure out that both polyhedra (sicid and gicid) have chi = -4 and -6 + 2 = -4. But that only holds if you don't merge coincident edges and vertices. 4 T C 08:36, 24 January 2010 (UTC)[reply]

Oh dear. There's yet another problem: do these polyhedra have duals? Let's just call them the small complex icosidodecacron and the great complex icosidodecacron like the uniform polyhedra. And - well - if they had duals, what would they look like? 4 T C 08:41, 24 January 2010 (UTC)[reply]

Without having given it much thought, I would think the dual of a compound would be the compound of the duals. That will most likely be just as messy as the originals, but if we accept the original as existing, we should accept the dual as existing too. --Tango (talk) 08:51, 24 January 2010 (UTC)[reply]

By your definition, the dual of sicid would be a compound of a small stellated dodecahedron with its stellation core - a dodecahedron - in the centre. Darn, coincident edges and vertices again. Then the dual of gicid would be a compound of a great dodecahedron with a great stellated dodecahedron outside it, completely swallowing it up - the duals are just as messy as the originals. 4 T C 08:54, 24 January 2010 (UTC)[reply]

Well, sicid's dual looks like gicid, and gicid's dual looks like a great stellated dodecahedron. (Not sure if I should tell all of you this, but I generated gicid as sicid's dual here, as you couldn't see the inside. Looks like Stella uses Tango's definition.) 4 T C 08:56, 24 January 2010 (UTC)[reply]

Who's Stella? I didn't define anything, I just naively applied the standard definition of the dual of a polyhedron - the definition still works in this weird world we're discussing, it just gets an equally weird result. --Tango (talk) 08:59, 24 January 2010 (UTC)[reply]

This is Stella. ;-) Sorry for not being clear about that. 4 T C 09:04, 24 January 2010 (UTC)[reply]

(undent) For completeness, here are some freshly baked dual images. However they suffer from the same problems!

4 T C 13:05, 24 January 2010 (UTC)[reply]

And could they be considered uniform? They satisfy the requirements, but something seems strange. 4 T C 08:45, 24 January 2010 (UTC)[reply]

MathWorld says yes - but I'm not sure. 4 T C 09:20, 24 January 2010 (UTC)[reply]

There really is something very sinister about these two polyhedra. I wonder if there are any more like them? 4 T C 08:45, 24 January 2010 (UTC)[reply]

Well, their duals of course. There are a lot - say, a dodecahedron with an interior great stellated dodecahedron, or a compound of a cube, an octahedron, and a cuboctahedron. 4 T C 09:20, 24 January 2010 (UTC)[reply]

Now I'm not even sure they're compounds, as no compound has such coincident edges and vertices. 4 T C 08:51, 24 January 2010 (UTC)[reply]

I don't think it really matters - you get the same problems with other compounds, so excluding this case form being a compound doesn't seem to gain much. --Tango (talk) 08:55, 24 January 2010 (UTC)[reply]

I meant excluding cases where all vertices and edges coincide. This excludes these two but leaves all the other uniform compounds intact. 4 T C 09:02, 24 January 2010 (UTC)[reply]

Whoever wrote Polyhedral compound seems to think you can have polyhedra that aren't 2-manifolds. Those pictures certainly aren't of 2-manifolds, and the first line says they are polyhedra. --Tango (talk) 08:55, 24 January 2010 (UTC)[reply]

While you can have polyhedra with chi > 2 that aren't polyhedra (like the great disnub dirhombidodecahedron), something is wrong with the article in my opinion. Oh well, that's what you get for having no proper definition of a polyhedron. 4 T C 08:58, 24 January 2010 (UTC)[reply]

These things are weird. Weird, weird, weird. 4 T C 09:10, 24 January 2010 (UTC)[reply]

So weird we'd better shove them under the rug! 4 T C 09:21, 24 January 2010 (UTC)[reply]

An interesting debate as to Euler characteristics and what consitutes a polyhedron is to be found in Lakatos' book Proofs and refutations. Tinfoilcat (talk) 12:52, 24 January 2010 (UTC)[reply]

Very interesting - there's even an image of a great stellated dodecahedron on the cover. (That is, if it isn't a great complex icosidodecacron.) 4 T C 12:57, 24 January 2010 (UTC)[reply]

Until Stella (software) was mentioned, in my naivety I assumed that the pics were of physical models, possibly copper-foil stained glass nicely soldered and with spherical bumps of gilt solder at the vertices - now that would be craftsmanship.→86.132.233.255 (talk) 13:39, 24 January 2010 (UTC)[reply]

If only I could really do that... ;-) 4 T C 08:12, 25 January 2010 (UTC)[reply]

January 25

Cryptography

I can't figure this out. Can someone else decrypt it?

9 ka 1f 2c 1t g1 sj g3 ni aa hm a2 ub dh g2 y6 1d8 ug 18q m3 dq 1i5 m6 18x 1fz 1bc ep 1e 1e g1 4r 1i kd uc g5 qq 43 p7 9b 5e f3 ce qt km 18n 16s

--J4\/4 <talk> 18:24, 25 January 2010 (UTC)[reply]

It is not possible to decrypt without knowing the key and encryption/decryption algorithm. More info is needed. 78.101.208.18 (talk) 20:48, 25 January 2010 (UTC)[reply]

I think he wants someone to codebreak (you know, like the NSA). --75.50.49.11 (talk) 22:57, 25 January 2010 (UTC)[reply]

Differential equation

I was given a differential equation to solve: 3y'=5y^(2/5) or something, over the domain -infinity to infinity. We're also given than y(-1)=2 and y(4)=32...but how can this be? Solutions are of the form y=(x+C)^(3/5), so there would have to be two different C values for x=-1 and x=4. Now I know that, if say x=0 is not allowed, the domain is split in two an each part of the domain gets a seperate C value...but why would this apply to this case here? —Preceding unsigned comment added by 173.179.59.66 (talk) 19:09, 25 January 2010 (UTC)[reply]

Your solution isn't one for that DE, and you should only need one initial condition for a first-order equation. Are you stating the problem correctly? (It's worth noting that your DE is autonomous; that's the source of the

x+C

form.) --Tardis (talk) 20:21, 25 January 2010 (UTC)[reply]

(ec) First note that the solution you wrote is not correct (have you checked it?). To find a solution, try the ansatz y(x):=c|x|^αsgn(x) (which simply writes cx^α in case α is a negative integer) and determine c and α plugging y(x) it into the equation. But first go and check the equation you were given: I bet it was 3y'=5|y|^2/5, with the absolute value. Since the equation is autonomous (no x appears in it), y(x-a) is also a solution, for any real a. Not only: you may take y(x)=0 in some interval [a,b] and attach to it solutions of the above form for x>b and x<a vanishing at a and respectively b (check that such a function satisfies the ODE at any real x). For your problem, take a=-1 and b=4. You may be confused because the initial value problem for this equation does not have unicity, but note that the Cauchy-Lipschitz-Lindelöf-Picard-&c.. unicity theorem does not apply, because the RHS lacks the Lipschitz condition. pma.--84.220.118.69 (talk) 20:22, 25 January 2010 (UTC)[reply]

Step by step:

3y'=5y^{\frac {2}{5}}

3{\frac {dy}{dx}}=5y^{\frac {2}{5}}

3dy=5y^{\frac {2}{5}}dx

dx={\frac {3}{5}}y^{-{\frac {2}{5}}}dy

x=\int {\frac {3}{5}}y^{-{\frac {2}{5}}}dy=y^{\frac {3}{5}}+C

y^{\frac {3}{5}}=x-C

y=(x-C)^{\frac {5}{3}}

Another solution is

y=0\,

so the general solutions can be written

y=-[x\leq C_{1}](C_{1}-x)^{\frac {5}{3}}+[C_{2}\leq x](x-C_{2})^{\frac {5}{3}}

using the Iverson bracket for notation, and assuming that

-\infty \leq C_{1}\leq C_{2}\leq \infty

.

Bo Jacoby (talk) 18:05, 26 January 2010 (UTC).[reply]

Topological Group Question

I'm having trouble figuring out this exercise: If G is a compact topological group, and g is in G, let A = {g⁰, g¹, g²,... }. Show that the closure of A is a subgroup of G. This is problem 3 in section 15 of Bredon's Topology and Geometry (p. 55).

I'm trying to show that g^-1 is in the closure of A and then I think the rest should be pretty straight forward. Since G is compact, the sequence g⁰, g¹, g²,... has to have a subsequence that converges, but I can't figure out how to prove that there's one that converges to g^-1. Rckrone (talk) 23:57, 25 January 2010 (UTC)[reply]

Maybe just show the closure K satisfies gK=K. gK ⊆ K since a subsequence times g is still a subsequence. K ⊆ gK, because a convergent subsequence doesn't change its limit when you remove g^0, and so a convergent subsequence (minus at most one term) divided by g is still a convergent subsequence. JackSchmidt (talk) 01:18, 26 January 2010 (UTC)[reply]

For showing K ⊆ gK, wouldn't you also need to show that g⁰ is in gK (which is equivalent to showing g^-1 is in K)? I think what you did is not dependent on G being compact, and the property doesn't necessarily hold when compactness is removed. Rckrone (talk) 01:32, 26 January 2010 (UTC)[reply]

As far as equivalence goes, yes of course, that's how logic works. I show something equivalent to what you want is true, so what you want is true. What I did is very much dependent on K being compact, otherwise why would K have any points besides A in it? In other words, where do all the convergent subsequences come from? JackSchmidt (talk) 01:49, 26 January 2010 (UTC)[reply]

I think you misunderstood my objection. You did not show that g⁰ is in gK, which is the crux of the problem. Rckrone (talk) 04:40, 26 January 2010 (UTC)[reply]

(ec)The proposition is false if you don't assume compactness, so it must be used somehow. First, eliminate the case where A is finite since then g is finite order. Then by compactness, let x be a limit point. Let g^n_i be a subsequence that converges to x. It shouldn't be hard to show that the set g^n_i-n_j (i>j) has 1 as a limit point. So 1 is a limit point of A and from there is trivial to show that g^-1 is a limit point of A. I think that will work as an outline at least.--RDBury (talk) 01:46, 26 January 2010 (UTC)[reply]

The problem I have is that if g^n_i and g^n_j are "close" I don't know that implies that g^n_i-n_j and 1 are "close". For example suppose in R that gⁿ = 1/n. Obviously that's not a group, but I'm not sure what about a topological group makes something like that not happen. Rckrone (talk) 02:28, 26 January 2010 (UTC)[reply]

Multiplying by g^−n_j is a homeomorphism. Algebraist 02:33, 26 January 2010 (UTC)[reply]

Note that a topological group is a uniform space, and that "x and y are close" exactly means that xy^-1 is close to 1. --pm a 09:15, 26 January 2010 (UTC)[reply]

Sorry if this is just me being dense, but I'm not sure what to do with that. Say I have some open neighborhood U of 1. I want to show that there's some g^m in U (m>0). So I try to show that there's some i and j, i<j such that gⁱ(U) contains g^j. One way that came to mind was to argue that the gⁱ(U)'s covered the closure of A. But I don't how to show that. Rckrone (talk) 03:16, 26 January 2010 (UTC)[reply]

Ok I think I got it. For any neighborhood U of 1 you can find a symmetric open subset of U, call it V. For any point x not A but in the closure of A, there is a subsequence that converges to x, so there's a gⁿ in x(V) so y = x^-1gⁿ is in V. gⁿ = xy so gⁿy^-1 = x. y^-1 is also in V, so x is in gⁿ(V). That shows that the gⁱ(V)'s and therefore the gⁱ(U)'s cover the closure of A, which is compact, so there's a finite subcover. Then for all open U around 1, there's some g^j in gⁱ(U) with j>i, so g^j-i is in U. So there's a subsequence that converges to 1, and from that a subsequence that converges to gⁿ for each n<0. Thanks for the nudges. Rckrone (talk) 04:19, 26 January 2010 (UTC)[reply]

Just a small detail: since G is not assumed to be first countable, it may fail to be sequentially compact. I'd like more your proof rephrased this way: for any nbd U of the identity there exists n≥0, such that ggⁿ ∈U. This can be written as gⁿ ∈ g^-1 U, and reads exactly : g^-1 belongs to the closure of A. (any nbd of g^-1 meets A) pma. --84.220.118.69 (talk) 08:05, 26 January 2010 (UTC)[reply]

That makes sense but I'm confused about sequential compactness. If a space is compact, then any net has subnet that converges. Isn't a sequence a net? So wouldn't any sequence in a compact space have a convergent subsequence? Obviously I'm doing something wrong. Rckrone (talk) 06:27, 27 January 2010 (UTC)[reply]

January 26

Inverse Trigonometric Identity Prove

Hello. How would you prove $\arctan m+\arctan n=\arccos {\frac {1-mn}{\sqrt {(1+m^{2})(1+n^{2})}}}$ ? Thanks in advance. --Mayfare (talk) 02:11, 26 January 2010 (UTC)[reply]

Take the tangent of both sides. The lhs can then be evaluated using the tangent angle addition formula; you should get

{\frac {m+n}{1-mn}}

after canceling tans with arctans. Let the messy expression inside arccos be X, and define θ=arccos(X), or X=cos(θ). Then use

\tan ^{2}(\theta )+1=\sec ^{2}(\theta )\,

. You know sec(θ)=1/X. A bunch of messy algebra confirms that the rhs equals the lhs. --COVIZAPIBETEFOKY (talk) 02:30, 26 January 2010 (UTC)[reply]

I like your proof. Do we have to apply tangent on both sides since that would be crossing the left and right sides? --Mayfare (talk) 02:54, 26 January 2010 (UTC)[reply]

You always have to do the same thing to both sides, otherwise the two sides would no longer be equal. --Tango (talk) 04:32, 26 January 2010 (UTC)[reply]

Alternative geometric approach: draw a right angled triangle PQR with base 1 and height m. Using same base but going in opposite direction (i.e. "down" instead of "up", draw a right angled triangle PQS with base 1 and height n. You now have a triangle PRS with sides PR = √(1+m²), PS = √(1+n²) and RS = m+n. The angle opposite side RS is arctan(m)+arctan(n). Now apply the cosine rule. Gandalf61 (talk) 14:28, 26 January 2010 (UTC)[reply]

Cross ratio equal to 1/2tan^2 of spherical distnce

Hi all,

I wasn't sure whether to ask this here or not, I was hoping to sort it out myself but after 4 days thinking about it and so far had no such luck, it's clear that I'm not going to make any further progress without a little help - I don't think I can quite get my head around the geometry that's in play.

If u,v $\in \mathbb {C}$ correspond to points P, Q on $S^{2}$ , and d denotes the angular distance from P to Q on $S^{2}$ , show that $-\tan ^{2}({\frac {d}{2}})$ is the cross ratio of the points $u,v,{\frac {-1}{u^{*}}},{\frac {-1}{v^{*}}}$ , taken in an appropriate order (which you should specify). (The star denotes complex conjugation - I'm not sure how to do the 'bar' in latex!)

Now I'm useless at geometry, but if I recall correctly, ${\frac {-1}{u^{*}}}$ would correspond to the stereographic projection of the point (-P), right? And likewise with v - other than that however, I really can't see a smart way to do this. I certainly don't want to try all 6 permutations of the 4 points and see what pops up on the cross ratio, but at the same time I can't see intuitively where the $-\tan ^{2}({\frac {d}{2}})$ could have come from in order to try and work out how to take the cross ratio to get the desired result. I'm aware that the angle between the 2 points P and Q is equal to d, but I can't seem to work anything out in the complex plane rather than the sphere. Please help!

Many thanks in advance! Mathmos6 (talk) 04:22, 26 January 2010 (UTC)[reply]

Cross-ratio is a projective invariant i.e. it is unchanged by projective transformations. So you can rotate

S^{2}

to place u and v at convenient points without changing the cross-ratio. For example, you can place u at the origin and v at a point x on the real axis. Then -1/u* is at infinity, -1/v* is at -1/x, and the cross-ratio is -x² (I think). Gandalf61 (talk) 11:38, 26 January 2010 (UTC)[reply]

I was wondering...

Is there a set numbers considered as the infinitesimal set? --Neptunerover (talk) 07:09, 26 January 2010 (UTC)[reply]

No. You can talk about the subset of infinitesimals within some number system, but that's all. An infinitesimal is a number that, however many times you add it to itself, will never give a result greater than 1 (or any other finite number). What infinitesimals exist will depend on what number system you are working in. In all the commonly used systems (ie. subsets of the complex numbers) the only infinitesimal is 0 (which is usually explicitly excluded when talking about infinitesimals). --Tango (talk) 07:43, 26 January 2010 (UTC)[reply]

I was thinking of within the set of rational numbers. --Neptunerover (talk) 07:55, 26 January 2010 (UTC)[reply]

If you wish to see concretely an infinitesimal among rationals, call it x and just add it to them as a tascendental extension. You'll find the ordered field of rational functions Q(x), where the order is such that 0<x<q for any positive rational q, and in general for two elements, f<g means that f<g as functions in a right neighborhood of 0.--pm a 09:28, 26 January 2010 (UTC)[reply]

Thank you. That darn f of x stuff is the semester I had an algebra teacher who taught straight out of the textbook, which lost me from the beginning. I don't believe those books are intended to make sense on there own, otherwise there would be no need for the class. --Neptunerover (talk) 09:41, 26 January 2010 (UTC)[reply]

One should emphasise: that is among rationals, not within rationals. Q(x) is not a subset of Q. Zero is the only infinitesimal within the rationals. --Tango (talk) 10:00, 26 January 2010 (UTC)[reply]

More emphasis than that would be aragoto style. --pm a 11:20, 26 January 2010 (UTC)[reply]

Normed Spaces

I want to find out the largest c such that $\lVert \alpha _{1}e_{1}+\alpha _{2}e_{2}\rVert \geq c(|\alpha _{1}|+|\alpha _{2}|)$ where ${e_{1},e_{2}}$ is the standard basis of $R^{2}(R)$ endowed with the standard norm. How should I proceed? I am interested in the general way of finding out such a c in case of arbitrary bases or normed spaces. Thanks.-Shahab (talk) 08:41, 26 January 2010 (UTC)[reply]

I assume you want c independent from α₁ and α₂. So you want to compare the L¹ and L² norms in R². Use the Cauchy-Schwarz inequality with the two vectors (1,1) and (α₁, α₂):

|α₁| + |α₂|=1|α₁| + 1|α₂| ≤ (1² + 1²)^1/2(|α₁|² + |α₂|²)^1/2=2^1/2 (|α₁|² + |α₂|²)^1/2. Recall that the CS inequality is an equality whenever the two vectors are linearly dependent (here it means |α₁|=|α₂|); this tells you that c:=2^-1/2 is the largest. To compare two L^p norms use analogously the Minkowski inequality. In general, the problem of computing the best constant of a normed space embedding may be a very hard problem in the calculus of variations. --pm a 09:05, 26 January 2010 (UTC)[reply]

Can you elaborate on why c:=2^-1/2 is the largest part, not on equality in CS iff vectors are LD but how you use this to conclude that c:=2^-1/2 is the largest. I intutively understand it but I am having trouble deriving it rigorously. Thanks for the rest.-Shahab (talk) 10:25, 26 January 2010 (UTC)[reply]

You want the largest c with the property that: for all

\alpha _{1}

and

\alpha _{2},

there holds

\lVert \alpha _{1}e_{1}+\alpha _{2}e_{2}\rVert \geq c(|\alpha _{1}|+|\alpha _{2}|).

The number

2^{-1/2}

has this property; any number larger than

2^{-1/2}

has not, because the property fails when tested with (1,1).

We can also say it in another way: since the inequality is trivially satisfied for (α₁, α₂)=(0,0), you may forget about (0,0) and ask it just for all (α₁, α₂)≠(0,0). You may then divide the RHS by the positive quantity

|\alpha _{1}|+|\alpha _{2}|,

and if you think a little you see that what you are looking for is exactly the greater lower bound of the numbers

\scriptstyle {\frac {\lVert \alpha _{1}e_{1}+\alpha _{2}e_{2}\rVert }{(|\alpha _{1}|+|\alpha _{2}|)}}

among all (α₁, α₂)≠(0,0). Here, we even have a minimum, which is reached by (1,1). --pm a 11:03, 26 January 2010 (UTC)[reply]

Thanks. It's all clear now. Have a nice day-Shahab (talk) 11:10, 26 January 2010 (UTC)[reply]

A loxodromoid?

Maybe you do have more specialists here? In the Reference desk of the Finnish Wikipedia we got a question like this; I translate it here:
"Does a loxodrome have a 2D counterpart (or is it even possible for it to have such one)? A spiral is very similar, indeed, but, on a circle, its other end crosses the circumference while a loxodrome is wholly located on the surface of a sphere turning towards the poles of it."
I suppose, this is a matter of the qualities of the polarities of a sphere and a circle? --Watsimous (talk) 17:42, 26 January 2010 (UTC)[reply]

There is a generalization here (if you speak French as well as English and Finish), but it's a loxodrome defined on surfaces other than a sphere, not a loxodromic surface. It may be possible to invent something like that but question is whether anyone has seriously proposed it as a useful concept and studied it. Mathcurve.com is, imo, pretty complete with this type of thing so if it isn't there the answer is probably no.--RDBury (talk) 20:02, 26 January 2010 (UTC)[reply]

The only thing I can think of would be to omit, say, y from the parametric equations for a normal loxodrome; then it will trace a sinusoidal path within a circle and terminate at two opposite points. That's assuming that your correspondent means by a "2D counterpart" a loxodrome-like curve within the circle instead of on the sphere, rather than a 2-manifold based on the loxodrome. --Tardis (talk) 21:33, 26 January 2010 (UTC)[reply]

January 27

Calculating the area of a triangle while on a coordinate system

Say there are three points on a cartesian coordinate system that form a triangle. What is the formula that would express the area? The normal 1/2*base*height doesn't seem like it would apply here and Triangle#Using_coordinates is too advanced. My programming professor linked to this site as a hint but I fail to see how that helps. Angles are not known and how is it possible to add two points together? 198.188.150.134 (talk) 07:48, 27 January 2010 (UTC)[reply]

Heron's formula gives the area in terms of the length of sides and the semi-perimeter (half the total). You can find the length of each side by using Pythagoras' theorem (read this section) on each pair of co-ordinates. If your points are in 3-D space, you need to extend the Pythagoras formula (just square the x-difference, y-difference and z-difference, add them together, and take the square root for the length of that side). Dbfirs 08:02, 27 January 2010 (UTC)[reply]

You can link to a section using internal links. Also, your link doesn't work because the | character is extraneous in external links. -- Meni Rosenfeld (talk) 08:22, 27 January 2010 (UTC) [reply]

Triangle#Using_coordinates isn't "too advanced", it just covers several different cases and uses determinant notation to write it more compactly. The formula you need (if the triangles are in a 2D plane) is

{\textrm {Area}}={\big |}(x_{A}-x_{C})(y_{B}-y_{A})-(x_{A}-x_{B})(y_{C}-y_{A}){\big |}/2

where

|t|

is the absolute value of t. -- Meni Rosenfeld (talk) 08:16, 27 January 2010 (UTC)[reply]

Thank you, you guys are awesome! I love Wikipedia!! 198.188.150.134 (talk) 08:24, 27 January 2010 (UTC)[reply]