Spirograph

Spirograph

Inventor(s)	Denys Fisher
Company	Hasbro
Country	United Kingdom
Availability	1965–present
Materials	Plastic
Official website

A Spirograph is a geometric drawing toy that produces mathematical roulette curves of the variety technically known as hypotrochoids and epitrochoids. It was developed by British engineer Denys Fisher and first sold in 1965.

"Spirograph" has also been used to describe a variety of software applications that display similar curves. It has also been applied to the class of curves that can be produced with the drawing equipment, and therefore may be regarded as a synonym of hypotrochoid. The name has been a registered trademark of Hasbro, Inc., since it bought the Denys Fisher company.

History

The mathematician Bruno Abakanowicz invented the spirograph between 1881 and 1900. It was used to for calculating an area delimited by curves. Drawing toys based on gears have been around since at least 1908, when The Marvelous Wondergraph was advertised in the Sears catalog. An article describing how to make a Wondergraph drawing machine appeared in the Boys Mechanic publication in 1913. The Spirograph itself was developed by the British engineer Denys Fisher, who exhibited at the 1965 Nuremberg International Toy Fair. It was subsequently produced by his company. US distribution rights were acquired by Kenner, Inc., which introduced it to the United States market in 1966 and promoted it as a creative children's toy.

In 1968, Kenner introduced Spirotot, a less complex version of Spirograph, for preschool-age children too young for Spirograph.

Operation

Several Spirograph designs drawn with a Spirograph set

The original US-released Spirograph consisted of two different-sized plastic rings, with gear teeth on both the inside and outside of their circumferences. They were pinned to a cardboard backing with pins, and any of several provided gearwheels, which had holes provided for a ballpoint pen to extend through them to an underlying paper writing surface. It could be spun around to make geometric shapes on the underlying paper medium. Later, the Super-Spirograph consisted of a set of plastic gears and other interlocking shape-segments such as rings, triangles, or straight bars. It has several sizes of gears and shapes, and all edges have teeth to engage any other piece. For instance, smaller gears fit inside the larger rings, but also can engage the outside of the rings in such a fashion that they rotate around the inside or along the outside edge of the rings.

To use it, a sheet of paper is placed on a heavy cardboard backing, and one of the plastic pieces—known as a stator—is secured via pins or reusable adhesive to the paper and cardboard. Another plastic piece—called the rotor—is placed so that its teeth engage with those of the pinned piece. For example, a ring may be pinned to the paper and a small gear placed inside the ring. The number of arrangements possible by combining different gears is very large. The point of a pen is placed in one of the holes of the rotor. As the rotor is moved, the pen traces out a curve. The pen is used both to draw and to provide locomotive force; some practice is required before the Spirograph can be operated without disengaging the stator and rotor. More intricate and unusual-shaped patterns may be made through the use of both hands, one to draw and one to guide the pieces. It is possible to move several pieces in relation to each other (say, the triangle around the ring, with a circle "climbing" from the ring onto the triangle), but this requires concentration or even additional assistance from other artists.

Mathematical basis

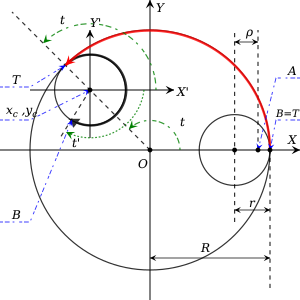
Consider a fixed circle $C_{1}$ of radius $R$ centered at the origin. A smaller circle $C_{2}$ of radius $r<R$ is rolling inside $C_{1}$ and it is tangent to $C_{1}$. The inner circle cannot slip since teeth are present in a real Spirograph. Now assume that a point $A$ that corresponds to hole in the inner circle of the Spirograph is located at the distance $\rho <r$ from the center of $C_{2}$. Without loss of generality it can be assumed that at the initial moment the point $A$ was on the $X$-axis. In order to find the trajectory created by a Spirograph, follow $A$ as the inner circle is set in motion.

Now mark two points $T$ on $C_{1}$ and $B$ on $C_{2}$. The point $T$ indicates where two circles are tangent all the time. Point $B$ however will travel on $C_{2}$ and its initial location coincides with $T$. After setting $C_{2}$ in motion counterclockwise, there is a clockwise rotation with respect to its center. The distances that point $B$ traverses on the small circle is the same as the distance that the tangent point $T$ travels on the large circle due to absence of any slipping effects.

Now the new (relative) system of coordinates $({\hat {X}},{\hat {Y}})$ with its origin at the center of $C_{2}$ and its axes parallel to $X$ and $Y$ is observable. If the parameter $t$ is defined as the angle by which the tangent point $T$ rotates on $C_{1}$ and ${\hat {t}}$ is the angle by which $C_{2}$ rotates (i.e. by which $B$ travels) in the relative system of coordinates, then the distances traveled by $B$ and $T$ along their respective circles must be the same (no slipping). Therefore

$tR=(t-{\hat {t}})r$

or equivalently

${\hat {t}}=-{\frac {R-r}{r}}t.$

It is common to assume that a counterclockwise motion results in a positive change of angle and a clockwise one will correspond to a negative change of angle. A minus sign in the above formula. (${\hat {t}}<0$)to accommodate this convention.

Let $(x_{c},y_{c})$ be the coordinates of the center of $C_{2}$ in the absolute system of coordinates. Then $R-r$ represents the radius of the trajectory of the center of the inner circle, and

${\begin{array}{rcl}x_{c}&=&(R-r)\cos t,\\y_{c}&=&(R-r)\sin t.\end{array}}$

The coordinates of $A$ in the new system are $({\hat {x}},{\hat {y}})$ and they obey the regular law of circular motion (the angle of rotation in the relative system is ${\hat {t}}$):

${\begin{array}{rcl}{\hat {x}}&=&\rho \cos {\hat {t}},\\{\hat {y}}&=&\rho \sin {\hat {t}}.\end{array}}$

In order to obtain the trajectory of $A$ in the absolute (old) system of coordinates, add these two motions:

${\begin{array}{rcrcl}x&=&{\hat {x}}+x_{c}&=&(R-r)\cos t+\rho \cos {\hat {t}},\\y&=&{\hat {y}}+y_{c}&=&(R-r)\sin t+\rho \sin {\hat {t}},\\\end{array}}$

where $\rho$ is defined above.

Now, use the relation between $t$ and ${\hat {t}}$ as discussed above to obtain equations describing the trajectory of point $A$ in terms of one parameter $t$:

${\begin{array}{rcrcl}x&=&{\hat {x}}+x_{c}&=&(R-r)\cos t+\rho \cos {\frac {R-r}{r}}t,\\[4pt]y&=&{\hat {y}}+y_{c}&=&(R-r)\sin t-\rho \sin {\frac {R-r}{r}}t.\\\end{array}}$

(using the fact that function $sin$ is odd)

It is convenient to represent the equation above in terms the radius $R$ of the largest circle and dimensionless parameters describing the structure of the Spirograph. Namely, let

$l={\frac {\rho }{r}}$

and

$k={\frac {r}{R}}.$

The parameter $0\leq l\leq 1$ represents how far the point $A$ is located from the center of the inner circle. At the same time, $0\leq k\leq 1$ represents how big the inner circle is with respect to the large one.

It is now observed that

${\frac {\rho }{R}}=lk,$

and therefore the trajectory equations take form of

${\begin{array}{rcl}x(t)&=&R\left[(1-k)\cos t+lk\cos {\frac {1-k}{k}}t\right],\\[4pt]y(t)&=&R\left[(1-k)\sin t-lk\sin {\frac {1-k}{k}}t\right].\\\end{array}}$

Parameter $R$ is a scaling parameter and will not affect the structure of the Spirograph. It is interesting to note that two extreme cases of $k=0$ and $k=1$ will result in degenerate trajectories of the Spirograph. Namely when $k=0$ we will have a simple circle of radius $R$. And indeed this case corresponds to the case when the inner circle is shrunk into a point. (Division by $k=0$ in the formula is not a problem since both $\sin$ and $\cos$ are bounded functions).

The other extreme case $k=1$ corresponds to the inner circle matching the large circle. In this case the trajectory is a single point since the inner circle is too large to roll without slipping.

If $l=1$ then it is the case when the point $A$ is on the circumference of the inner circle. In this case the trajectories are called hypocycloids and the equations will match the one describing a hypocycloid.

See also

• Guilloché
• Harmonograph
• Spirograph Nebula, a planetary nebula that displays delicate, spirograph-like filigree.
• List of periodic functions

External links

• Hasbro Spirograph site
• HTML5 Interactive Spirograph Creator
• A Spirograph software for MS Windows