Time crystal
This article may be too technical for most readers to understand. (March 2024) |
| Condensed matter physics |
|---|
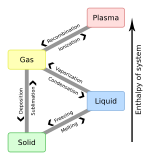
 |
| Time |
|---|
 |
In condensed matter physics, a time crystal is a quantum system of particles whose lowest-energy state is one in which the particles are in repetitive motion. The system cannot lose energy to the environment and come to rest because it is already in its quantum ground state. Time crystals were first proposed theoretically by Frank Wilczek in 2012 as a time-based analogue to common crystals – whereas the atoms in crystals are arranged periodically in space, the atoms in a time crystal are arranged periodically in both space and time.[1] Several different groups have demonstrated matter with stable periodic evolution in systems that are periodically driven.[2][3][4][5] In terms of practical use, time crystals may one day be used as quantum computer memory.[6]
The existence of crystals in nature is a manifestation of spontaneous symmetry breaking, which occurs when the lowest-energy state of a system is less symmetrical than the equations governing the system. In the crystal ground state, the continuous translational symmetry in space is broken and replaced by the lower discrete symmetry of the periodic crystal. As the laws of physics are symmetrical under continuous translations in time as well as space, the question arose in 2012 as to whether it is possible to break symmetry temporally, and thus create a "time crystal" that is resistant to entropy.[1]
If a discrete time-translation symmetry is broken (which may be realized in periodically driven systems), then the system is referred to as a discrete time crystal. A discrete time crystal never reaches thermal equilibrium, as it is a type (or phase) of non-equilibrium matter. Breaking of time symmetry can only occur in non-equilibrium systems.[5] Discrete time crystals have in fact been observed in physics laboratories as early as 2016. One example of a time crystal, which demonstrates non-equilibrium, broken time symmetry is a constantly rotating ring of charged ions in an otherwise lowest-energy state.[6]
Concept
[edit]Ordinary (non-time) crystals form through spontaneous symmetry breaking related to a spatial symmetry. Such processes can produce materials with interesting properties, such as diamonds, salt crystals, and ferromagnetic metals. By analogy, a time crystal arises through the spontaneous breaking of a time-translation symmetry. A time crystal can be informally defined as a time-periodic self-organizing structure. While an ordinary crystal is periodic (has a repeating structure) in space, a time crystal has a repeating structure in time. A time crystal is periodic in time in the same sense that the pendulum in a pendulum-driven clock is periodic in time. Unlike a pendulum, a time crystal "spontaneously" self-organizes into robust periodic motion (breaking a temporal symmetry).[7]
Time-translation symmetry
[edit]Symmetries in nature lead directly to conservation laws, something which is precisely formulated by Noether's theorem.[8]
The basic idea of time-translation symmetry is that a translation in time has no effect on physical laws, i.e. that the laws of nature that apply today were the same in the past and will be the same in the future.[9] This symmetry implies the conservation of energy.[10]
Broken symmetry in normal crystals
[edit]
Common crystals exhibit broken translation symmetry: they have repeated patterns in space and are not invariant under arbitrary translations or rotations. The laws of physics are unchanged by arbitrary translations and rotations. However, if we hold fixed the atoms of a crystal, the dynamics of an electron or other particle in the crystal depend on how it moves relative to the crystal, and particle momentum can change by interacting with the atoms of a crystal — for example in Umklapp processes.[11] Quasimomentum, however, is conserved in a perfect crystal.[12]
Time crystals show a broken symmetry analogous to a discrete space-translation symmetry breaking. For example,[citation needed] the molecules of a liquid freezing on the surface of a crystal can align with the molecules of the crystal, but with a pattern less symmetric than the crystal: it breaks the initial symmetry. This broken symmetry exhibits three important characteristics:[citation needed]
- the system has a lower symmetry than the underlying arrangement of the crystal,
- the system exhibits spatial and temporal long-range order (unlike a local and intermittent order in a liquid near the surface of a crystal),
- it is the result of interactions between the constituents of the system, which align themselves relative to each other.
Broken symmetry in discrete time crystals (DTC)
[edit]Time crystals seem to break time-translation symmetry and have repeated patterns in time even if the laws of the system are invariant by translation of time. The time crystals that are experimentally realized show discrete time-translation symmetry breaking, not the continuous one: they are periodically driven systems oscillating at a fraction of the frequency of the driving force. (According to Philip Ball, DTC are so-called because "their periodicity is a discrete, integer multiple of the driving period".[13])
The initial symmetry, which is the discrete time-translation symmetry () with , is spontaneously broken to the lower discrete time-translation symmetry with , where is time, the driving period, an integer.[14]
Many systems can show behaviors of spontaneous time-translation symmetry breaking but may not be discrete (or Floquet) time crystals: convection cells, oscillating chemical reactions, aerodynamic flutter, and subharmonic response to a periodic driving force such as the Faraday instability, NMR spin echos, parametric down-conversion, and period-doubled nonlinear dynamical systems.[14]
However, discrete (or Floquet) time crystals are unique in that they follow a strict definition of discrete time-translation symmetry breaking:[15]
- it is a broken symmetry – the system shows oscillations with a period longer than the driving force,
- the system is in crypto-equilibrium – these oscillations generate no entropy, and a time-dependent frame can be found in which the system is indistinguishable from an equilibrium when measured stroboscopically[15] (which is not the case of convection cells, oscillating chemical reactions and aerodynamic flutter),
- the system exhibits long-range order – the oscillations are in phase (synchronized) over arbitrarily long distances and time.
Moreover, the broken symmetry in time crystals is the result of many-body interactions: the order is the consequence of a collective process, just like in spatial crystals.[14] This is not the case for NMR spin echos.
These characteristics makes discrete time crystals analogous to spatial crystals as described above and may be considered a novel type or phase of nonequilibrium matter.[14]
Thermodynamics
[edit]Time crystals do not violate the laws of thermodynamics: energy in the overall system is conserved, such a crystal does not spontaneously convert thermal energy into mechanical work, and it cannot serve as a perpetual store of work. But it may change perpetually in a fixed pattern in time for as long as the system can be maintained. They possess "motion without energy"[16]—their apparent motion does not represent conventional kinetic energy.[17] Recent experimental advances in probing discrete time crystals in their periodically driven nonequilibrium states have led to the beginning exploration of novel phases of nonequilibrium matter.[14]
Time crystals do not evade the Second Law of Thermodynamics,[18] although they spontaneously break "time-translation symmetry", the usual rule that a stable object will remain the same throughout time. In thermodynamics, a time crystal's entropy, understood as a measure of disorder in the system, remains stationary over time, marginally satisfying the second law of thermodynamics by not decreasing.[19][20]
History
[edit]
The idea of a quantized time crystal was theorized in 2012 by Frank Wilczek,[21][22] a Nobel laureate and professor at MIT. In 2013, Xiang Zhang, a nanoengineer at University of California, Berkeley, and his team proposed creating a time crystal in the form of a constantly rotating ring of charged ions.[23][24]
In response to Wilczek and Zhang, Patrick Bruno (European Synchrotron Radiation Facility) and Masaki Oshikawa (University of Tokyo) published several articles stating that space–time crystals were impossible.[25][26]
Subsequent work developed more precise definitions of time-translation symmetry-breaking, which ultimately led to the Watanabe–Oshikawa "no-go" statement that quantum space–time crystals in equilibrium are not possible.[27][28] Later work restricted the scope of Watanabe and Oshikawa: strictly speaking, they showed that long-range order in both space and time is not possible in equilibrium, but breaking of time-translation symmetry alone is still possible.[29][30][31]
Several realizations of time crystals, which avoid the equilibrium no-go arguments, were later proposed.[32] In 2014 Krzysztof Sacha at Jagiellonian University in Kraków predicted the behaviour of discrete time crystals in a periodically driven system with "an ultracold atomic cloud bouncing on an oscillating mirror".[33][34]
In 2016, research groups at Princeton and at Santa Barbara independently suggested that periodically driven quantum spin systems could show similar behaviour.[35] Also in 2016, Norman Yao at Berkeley and colleagues proposed a different way to create discrete time crystals in spin systems.[36] These ideas were successful and independently realized by two experimental teams: a group led by Harvard's Mikhail Lukin[37] and a group led by Christopher Monroe at University of Maryland.[38] Both experiments were published in the same issue of Nature in March 2017.
Later, time crystals in open systems, so called dissipative time crystals, were proposed in several platforms breaking a discrete [39][40][41][42] and a continuous[43][44] time-translation symmetry. A dissipative time crystal was experimentally realized for the first time in 2021 by the group of Andreas Hemmerich at the Institute of Laser Physics at the University of Hamburg.[45] The researchers used a Bose–Einstein condensate strongly coupled to a dissipative optical cavity and the time crystal was demonstrated to spontaneously break discrete time-translation symmetry by periodically switching between two atomic density patterns.[45][46][47] In an earlier experiment in the group of Tilman Esslinger at ETH Zurich, limit cycle dynamics[48] was observed in 2019,[49] but evidence of robustness against perturbations and the spontaneous character of the time-translation symmetry breaking were not addressed.
In 2019, physicists Valerii Kozin and Oleksandr Kyriienko proved that, in theory, a permanent quantum time crystal can exist as an isolated system if the system contains unusual long-range multiparticle interactions. The original "no-go" argument only holds in the presence of typical short-range fields that decay as quickly as r−α for some α > 0. Kozin and Kyriienko instead analyzed a spin-1/2 many-body Hamiltonian with long-range multispin interactions, and showed it broke continuous time-translational symmetry. Certain spin correlations in the system oscillate in time, despite the system being closed and in a ground energy state. However, demonstrating such a system in practice might be prohibitively difficult,[50][51] and concerns about the physicality of the long-range nature of the model have been raised.[52]
In 2022, the Hamburg research team, supervised by Hans Keßler and Andreas Hemmerich, demonstrated, for the first time, a continuous dissipative time crystal exhibiting spontaneous breaking of continuous time-translation symmetry.[53][54][55][56]
In February 2024, a team from Dortmund University in Germany built a time crystal from indium gallium arsenide that lasted for 40 minutes, nearly 10 million times longer than the previous record of around 5 milliseconds. In addition, the lack of any decay suggests the crystal could have lasted even longer, stating that it could last "at least a few hours, perhaps even longer".[57][58][59][60][61]
Experiments
[edit]In October 2016, Christopher Monroe at the University of Maryland claimed to have created the world's first discrete time crystal. Using the ideas proposed by Yao et al.,[36] his team trapped a chain of 171Yb+ ions in a Paul trap, confined by radio-frequency electromagnetic fields. One of the two spin states was selected by a pair of laser beams. The lasers were pulsed, with the shape of the pulse controlled by an acousto-optic modulator, using the Tukey window to avoid too much energy at the wrong optical frequency. The hyperfine electron states in that setup, 2S1/2 |F = 0, mF = 0⟩ and |F = 1, mF = 0⟩, have very close energy levels, separated by 12.642831 GHz. Ten Doppler-cooled ions were placed in a line 0.025 mm long and coupled together.
The researchers observed a subharmonic oscillation of the drive. The experiment showed "rigidity" of the time crystal, where the oscillation frequency remained unchanged even when the time crystal was perturbed, and that it gained a frequency of its own and vibrated according to it (rather than only the frequency of the drive). However, once the perturbation or frequency of vibration grew too strong, the time crystal "melted" and lost this subharmonic oscillation, and it returned to the same state as before where it moved only with the induced frequency.[38]
Also in 2016, Mikhail Lukin at Harvard also reported the creation of a driven time crystal. His group used a diamond crystal doped with a high concentration of nitrogen-vacancy centers, which have strong dipole–dipole coupling and relatively long-lived spin coherence. This strongly interacting dipolar spin system was driven with microwave fields, and the ensemble spin state was determined with an optical (laser) field. It was observed that the spin polarization evolved at half the frequency of the microwave drive. The oscillations persisted for over 100 cycles. This subharmonic response to the drive frequency is seen as a signature of time-crystalline order.[37]
In May 2018, a group in Aalto University reported that they had observed the formation of a time quasicrystal and its phase transition to a continuous time crystal in a Helium-3 superfluid cooled to within one ten thousandth of a kelvin from absolute zero (0.0001 K). [62] On August 17, 2020 Nature Materials published a letter from the same group saying that for the first time they were able to observe interactions and the flow of constituent particles between two time crystals. [63]
In February 2021 a team at Max Planck Institute for Intelligent Systems described the creation of time crystal consisting of magnons and probed them under scanning transmission X-ray microscopy to capture the recurring periodic magnetization structure in the first known video record of such type.[64][65]
In July 2021, a team led by Andreas Hemmerich at the Institute of Laser Physics at the University of Hamburg presented the first realization of a time crystal in an open system, a so-called dissipative time crystal using ultracold atoms coupled to an optical cavity. The main achievement of this work is a positive application of dissipation – actually helping to stabilise the system's dynamics.[45][46][47]
In November 2021, a collaboration between Google and physicists from multiple universities reported the observation of a discrete time crystal on Google's Sycamore processor, a quantum computing device. A chip of 20 qubits was used to obtain a many-body localization configuration of up and down spins and then stimulated with a laser to achieve a periodically driven "Floquet" system where all up spins are flipped for down and vice-versa in periodic cycles which are multiples of the laser's frequency. While the laser is necessary to maintain the necessary environmental conditions, no energy is absorbed from the laser, so the system remains in a protected eigenstate order.[20][66]
Previously in June and November 2021 other teams had obtained virtual time crystals based on floquet systems under similar principles to those of the Google experiment, but on quantum simulators rather than quantum processors: first a group at the University of Maryland obtained time crystals on trapped-ions qubits using high frequency driving rather than many-body localization[67][68] and then a collaboration between TU Delft and TNO in the Netherlands called Qutech created time crystals from nuclear spins in carbon-13 nitrogen-vacancy (NV) centers on a diamond, attaining longer times but fewer qubits.[69][70]
In February 2022, a scientist at UC Riverside reported a dissipative time crystal akin to the system of July 2021 but all-optical, which allowed the scientist to operate it at room temperature. In this experiment injection locking was used to direct lasers at a specific frequency inside a microresonator creating a lattice trap for solitons at subharmonic frequencies.[71][72]
In March 2022, a new experiment studying time crystals on a quantum processor was performed by two physicists at the University of Melbourne, this time using IBM's Manhattan and Brooklyn quantum processors observing a total of 57 qubits.[73][74][75]
In June 2022, the observation of a continuous time crystal was reported by a team at the Institute of Laser Physics at the University of Hamburg, supervised by Hans Keßler and Andreas Hemmerich. In periodically driven systems, time-translation symmetry is broken into a discrete time-translation symmetry due to the drive. Discrete time crystals break this discrete time-translation symmetry by oscillating at a multiple of the drive frequency. In the new experiment, the drive (pump laser) was operated continuously, thus respecting the continuous time-translation symmetry. Instead of a subharmonic response, the system showed an oscillation with an intrinsic frequency and a time phase taking random values between 0 and 2π, as expected for spontaneous breaking of continuous time-translation symmetry. Moreover, the observed limit cycle oscillations were shown to be robust against perturbations of technical or fundamental character, such as quantum noise and, due to the openness of the system, fluctuations associated with dissipation. The system consisted of a Bose–Einstein condensate in an optical cavity, which was pumped with an optical standing wave oriented perpendicularly with regard to the cavity axis and was in a superradiant phase localizing at two bistable ground states between which it oscillated.[53][54][55][56]
References
[edit]- ^ a b Zakrzewski, Jakub (15 October 2012). "Viewpoint: Crystals of Time". physics.aps.org. APS Physics. Archived from the original on 2 February 2017.
- ^ Sacha, Krzysztof (2015). "Modeling spontaneous breaking of time-translation symmetry". Physical Review A. 91 (3): 033617. arXiv:1410.3638. Bibcode:2015PhRvA..91c3617S. doi:10.1103/PhysRevA.91.033617. ISSN 1050-2947. S2CID 118627872.
- ^ Khemani et al. (2016)
- ^ Else et al. (2016).
- ^ a b Richerme, Phil (January 18, 2017). "How to Create a Time Crystal". Physics. 10. American Physical Society: 5. Bibcode:2017PhyOJ..10....5R. doi:10.1103/Physics.10.5. Retrieved 5 April 2021.
- ^ a b "Physicists Create World's First Time Crystal".
- ^ Sacha, Krzysztof; Zakrzewski, Jakub (1 January 2018). "Time crystals: a review". Reports on Progress in Physics. 81 (1): 016401. arXiv:1704.03735. Bibcode:2018RPPh...81a6401S. doi:10.1088/1361-6633/aa8b38. PMID 28885193. S2CID 28224975.
- ^ Cao, Tian Yu (25 March 2004). Conceptual Foundations of Quantum Field Theory. Cambridge: Cambridge University Press. ISBN 978-0-521-60272-3. See p. 151.
- ^ Wilczek, Frank (16 July 2015). A Beautiful Question: Finding Nature's Deep Design. Penguin Books Limited. ISBN 978-1-84614-702-9. See Ch. 3.
- ^ Feng, Duan; Jin, Guojun (2005). Introduction to Condensed Matter Physics. singapore: World Scientific. ISBN 978-981-238-711-0. See p. 18.
- ^ Sólyom, Jenö (19 September 2007). Fundamentals of the Physics of Solids: Volume 1: Structure and Dynamics. Springer. ISBN 978-3-540-72600-5. See p. 193.
- ^ Sólyom, Jenö (19 September 2007). Fundamentals of the Physics of Solids: Volume 1: Structure and Dynamics. Springer. ISBN 978-3-540-72600-5. See p. 191.
- ^ Ball, Philip (July 17, 2018). "In search of time crystals". Physics World. 31 (7): 29. Bibcode:2018PhyW...31g..29B. doi:10.1088/2058-7058/31/7/32. S2CID 125917780. Retrieved September 6, 2021.
The "discrete" comes from the fact that their periodicity is a discrete, integer multiple of the driving period.
- ^ a b c d e Else, D. W.; Monroe, C.; Nayak, C.; Yao, N. Y. (March 2020). "Discrete Time Crystals". Annual Review of Condensed Matter Physics. 11: 467–499. arXiv:1905.13232. Bibcode:2020ARCMP..11..467E. doi:10.1146/annurev-conmatphys-031119-050658. S2CID 173188223.
- ^ a b Yao; Nayak (2018). "Time crystals in periodically driven systems". Physics Today. 71 (9): 40–47. arXiv:1811.06657. Bibcode:2018PhT....71i..40Y. doi:10.1063/PT.3.4020. ISSN 0031-9228. S2CID 119433979.
- ^ Crew, Bec. "Time Crystals Might Exist After All – And They Could Break Space-Time Symmetry". ScienceAlert. Retrieved 2017-09-21.
- ^ Cowen, Ron (2017-02-02). "'Time Crystals' Could Be a Legitimate Form of Perpetual Motion". Scientific American. Retrieved 2023-07-22.
- ^ "Google May Have Created an Unruly New State of Matter: Time Crystals". Popular Mechanics. Retrieved 4 August 2021.
- ^ Kubota, Taylor; University, Stanford. "Physicists create time crystals with quantum computers". phys.org. Retrieved 2021-12-03.
- ^ a b Mi, Xiao; Ippoliti, Matteo; Quintana, Chris; Greene, Ami; Chen, Zijun; Gross, Jonathan; Arute, Frank; Arya, Kunal; Atalaya, Juan; Babbush, Ryan; Bardin, Joseph C. (2022). "Time-Crystalline Eigenstate Order on a Quantum Processor". Nature. 601 (7894): 531–536. arXiv:2107.13571. Bibcode:2022Natur.601..531M. doi:10.1038/s41586-021-04257-w. ISSN 1476-4687. PMC 8791837. PMID 34847568.
- ^ Wilczek, Frank (2012). "Quantum Time Crystals". Physical Review Letters. 109 (16): 160401. arXiv:1202.2539. Bibcode:2012PhRvL.109p0401W. doi:10.1103/PhysRevLett.109.160401. ISSN 0031-9007. PMID 23215056. S2CID 1312256.
- ^ Shapere, Alfred; Wilczek, Frank (2012). "Classical Time Crystals". Physical Review Letters. 109 (16): 160402. arXiv:1202.2537. Bibcode:2012PhRvL.109p0402S. doi:10.1103/PhysRevLett.109.160402. ISSN 0031-9007. PMID 23215057. S2CID 4506464.
- ^ See Li et al. (2012a, 2012b).
- ^ Wolchover, Natalie (25 April 2013). "Perpetual Motion Test Could Amend Theory of Time". quantamagazine.org. Simons Foundation. Archived from the original on 2 February 2017.
- ^ See Bruno (2013a) and Bruno (2013b).
- ^ Thomas, Jessica (15 March 2013). "Notes from the Editors: The Aftermath of a Controversial Idea". physics.aps.org. APS Physics. Archived from the original on 2 February 2017.
- ^ See Nozières (2013), Yao et al. (2017), p. 1 and Volovik (2013).
- ^ Watanabe, Haruki; Oshikawa, Masaki (2015). "Absence of Quantum Time Crystals". Physical Review Letters. 114 (25): 251603. arXiv:1410.2143. Bibcode:2015PhRvL.114y1603W. doi:10.1103/PhysRevLett.114.251603. ISSN 0031-9007. PMID 26197119. S2CID 312538.
- ^ Medenjak, Marko; Buča, Berislav; Jaksch, Dieter (2020-07-20). "Isolated Heisenberg magnet as a quantum time crystal". Physical Review B. 102 (4): 041117. arXiv:1905.08266. Bibcode:2020PhRvB.102d1117M. doi:10.1103/physrevb.102.041117. ISSN 2469-9950. S2CID 160009779.
- ^ Khemani, Vedika; Moessner, Roderich; Sondhi, S. L. (23 October 2019). "A Brief History of Time Crystals". arXiv:1910.10745 [cond-mat.str-el].
- ^ Uhrich, P.; Defenu, N.; Jafari, R.; Halimeh, J. C. (2020). "Out-of-equilibrium phase diagram of long-range superconductors". Physical Review B. 101 (24): 245148. arXiv:1910.10715. Bibcode:2020PhRvB.101x5148U. doi:10.1103/physrevb.101.245148.
- ^ See Wilczek (2013b) and Yoshii et al. (2015).
- ^ Sacha, Krzysztof (2015). "Modeling spontaneous breaking of time-translation symmetry". Physical Review A. 91 (3): 033617. arXiv:1410.3638. Bibcode:2015PhRvA..91c3617S. doi:10.1103/PhysRevA.91.033617. ISSN 1050-2947. S2CID 118627872.
We show that an ultracold atomic cloud bouncing on an oscillating mirror can reveal spontaneous breaking of a discrete time-translation symmetry
- ^ Sacha, Krzysztof (2020). Time Crystals. Springer Series on Atomic, Optical, and Plasma Physics. Vol. 114. Springer. doi:10.1007/978-3-030-52523-1. ISBN 978-3-030-52522-4. S2CID 240770955.
- ^ See Khemani et al. (2016) and Else et al. (2016)
- ^ a b Yao, N. Y.; Potter, A. C.; Potirniche, I.-D.; Vishwanath, A. (2017). "Discrete Time Crystals: Rigidity, Criticality, and Realizations". Physical Review Letters. 118 (3): 030401. arXiv:1608.02589. Bibcode:2017PhRvL.118c0401Y. doi:10.1103/PhysRevLett.118.030401. ISSN 0031-9007. PMID 28157355. S2CID 206284432.
- ^ a b Choi, Soonwon; Choi, Joonhee; Landig, Renate; Kucsko, Georg; Zhou, Hengyun; Isoya, Junichi; Jelezko, Fedor; Onoda, Shinobu; Sumiya, Hitoshi; Khemani, Vedika; von Keyserlingk, Curt; Yao, Norman Y.; Demler, Eugene; Lukin, Mikhail D. (2017). "Observation of discrete time-crystalline order in a disordered dipolar many-body system". Nature. 543 (7644): 221–225. arXiv:1610.08057. Bibcode:2017Natur.543..221C. doi:10.1038/nature21426. ISSN 0028-0836. PMC 5349499. PMID 28277511.
- ^ a b Zhang, J.; Hess, P. W.; Kyprianidis, A.; Becker, P.; Lee, A.; Smith, J.; Pagano, G.; Potirniche, I.-D.; Potter, A. C.; Vishwanath, A.; Yao, N. Y.; Monroe, C. (2017). "Observation of a discrete time crystal". Nature. 543 (7644): 217–220. arXiv:1609.08684. Bibcode:2017Natur.543..217Z. doi:10.1038/nature21413. PMID 28277505. S2CID 4450646.
- ^ Iemini, Fernando; Russomanno, Angelo; Keeling, Jonathan; Schirò, Marco; Dalmonte, Marcello; Fazio, Rosario (16 July 2018). "Boundary time crystals". Phys. Rev. Lett. 121 (35301): 035301. arXiv:1708.05014. Bibcode:2018PhRvL.121c5301I. doi:10.1103/PhysRevLett.121.035301. PMID 30085780. S2CID 51683292.
- ^ Gong, Zongping; Hamazaki, Ryusuke; Ueda, Masahito (25 January 2018). "Discrete Time-Crystalline Order in Cavity and Circuit QED Systems". Phys. Rev. Lett. 120 (40404): 040404. arXiv:1708.01472. Bibcode:2018PhRvL.120d0404G. doi:10.1103/PhysRevLett.120.040404. PMID 29437420. S2CID 206307409.
- ^ Filippo Maria, Gambetta; Carollo, Federico; Marcuzzi, Matteo; Garrahan, Juan P.; Lesanovsky, Igor (8 January 2019). "Discrete Time Crystals in the Absence of Manifest Symmetries or Disorder in Open Quantum Systems". Phys. Rev. Lett. 122 (15701): 015701. arXiv:1807.10161. Bibcode:2019PhRvL.122a5701G. doi:10.1103/PhysRevLett.122.015701. PMID 31012672. S2CID 119187766.
- ^ Buča, Berislav; Jaksch, Dieter (2019-12-23). "Dissipation Induced Nonstationarity in a Quantum Gas". Physical Review Letters. 123 (26): 260401. arXiv:1905.12880. Bibcode:2019PhRvL.123z0401B. doi:10.1103/PhysRevLett.123.260401. PMID 31951440. S2CID 170079211.
- ^ Iemini, F.; Russomanno, A.; Keeling, J.; Schirò, M.; Dalmonte, M.; Fazio, R. (2018-07-16). "Boundary Time Crystals". Physical Review Letters. 121 (3): 035301. arXiv:1708.05014. Bibcode:2018PhRvL.121c5301I. doi:10.1103/PhysRevLett.121.035301. hdl:10023/14492. PMID 30085780. S2CID 51683292.
- ^ Buča, Berislav; Tindall, Joseph; Jaksch, Dieter (2019-04-15). "Non-stationary coherent quantum many-body dynamics through dissipation". Nature Communications. 10 (1): 1730. arXiv:1804.06744. Bibcode:2019NatCo..10.1730B. doi:10.1038/s41467-019-09757-y. ISSN 2041-1723. PMC 6465298. PMID 30988312.
- ^ a b c Keßler, Hans; Kongkhambut, Phatthamon; Georges, Christoph; Mathey, Ludwig; Cosme, Jayson G.; Hemmerich, Andreas (2021-07-19). "Observation of a Dissipative Time Crystal". Physical Review Letters. 127 (4): 043602. arXiv:2012.08885. Bibcode:2021PhRvL.127d3602K. doi:10.1103/PhysRevLett.127.043602. PMID 34355967. S2CID 229210935.
- ^ a b Gong, Zongping; Ueda, Masahito (2021-07-19). "Time Crystals in Open Systems". Physics. 14: 104. Bibcode:2021PhyOJ..14..104G. doi:10.1103/Physics.14.104. S2CID 244256783.
- ^ a b Ball, Philip (September 2021). "Quantum time crystals open up". Nature Materials. 20 (9): 1172. Bibcode:2021NatMa..20.1172B. doi:10.1038/s41563-021-01090-4. ISSN 1476-4660. PMID 34433935. S2CID 237299508.
- ^ Piazza, Francesco; Ritsch, Helmut (2015-10-15). "Self-Ordered Limit Cycles, Chaos, and Phase Slippage with a Superfluid inside an Optical Resonator". Physical Review Letters. 115 (16): 163601. arXiv:1507.08644. Bibcode:2015PhRvL.115p3601P. doi:10.1103/PhysRevLett.115.163601. PMID 26550874. S2CID 5080527.
- ^ Dogra, Nishant; Landini, Manuele; Kroeger, Katrin; Hruby, Lorenz; Donner, Tobias; Esslinger, Tilman (2019-12-20). "Dissipation-induced structural instability and chiral dynamics in a quantum gas". Science. 366 (6472): 1496–1499. arXiv:1901.05974. Bibcode:2019Sci...366.1496D. doi:10.1126/science.aaw4465. ISSN 0036-8075. PMID 31857481. S2CID 119283814.
- ^ Cho, Adrian (27 November 2019). "Back to the future: The original time crystal makes a comeback". Science. doi:10.1126/science.aba3793. Retrieved 19 March 2020.
- ^ Kozin, Valerii K.; Kyriienko, Oleksandr (2019-11-20). "Quantum Time Crystals from Hamiltonians with Long-Range Interactions". Physical Review Letters. 123 (21): 210602. arXiv:1907.07215. Bibcode:2019PhRvL.123u0602K. doi:10.1103/PhysRevLett.123.210602. ISSN 0031-9007. PMID 31809146. S2CID 197431242.
- ^ Khemani, Vedika; Moessner, Roderich; Sondhi, S. L. (2020). "Comment on 'Quantum Time Crystals from Hamiltonians with Long-Range Interactions'". arXiv:2001.11037 [cond-mat.str-el].
- ^ a b Kongkhambut, Phatthamon; Skulte, Jim; Mathey, Ludwig; Cosme, Jayson G.; Hemmerich, Andreas; Keßler, Hans (2022-08-05). "Observation of a continuous time crystal". Science. 377 (6606): 670–673. arXiv:2202.06980. Bibcode:2022Sci...377..670K. doi:10.1126/science.abo3382. ISSN 0036-8075. PMID 35679353. S2CID 246863968.
- ^ a b LeBlanc, Lindsay J. (2022-08-05). "Unleashing spontaneity in a time crystal". Science. 377 (6606): 576–577. Bibcode:2022Sci...377..576L. doi:10.1126/science.add2015. ISSN 0036-8075. PMID 35926056. S2CID 251349796.
- ^ a b "Researchers observe continuous time crystal". www.cui-advanced.uni-hamburg.de. Retrieved 2022-08-07.
- ^ a b Hamburg, University of (2022-07-03). "Physicists Create Continuous Time Crystal for the First Time". SciTechDaily. Retrieved 2022-08-07.
- ^ "Scientists Built a Time Crystal That Lasted for 40 Minutes. That's Astonishing". 24 February 2024.
- ^ "A Time Crystal Survived a Whopping 40 Minutes". 6 February 2024.
- ^ https://www.msn.com/en-ca/news/technology/scientists-built-a-time-crystal-that-lasted-for-40-minutes-that-s-astonishing/ar-BB1iODrc
- ^ "Radical New Time Crystal Revealed That Lasts Millions of Times Longer". 5 February 2024.
- ^ "Physicists develop highly robust time crystal".
- ^ Autti, S.; Eltsov, V. B.; Volovik, G. E. (May 2018). "Observation of a Time Quasicrystal and Its Transition to a Superfluid Time Crystal". Physical Review Letters. 120 (21): 215301. arXiv:1712.06877. Bibcode:2018PhRvL.120u5301A. doi:10.1103/PhysRevLett.120.215301. PMID 29883148. S2CID 46997186.
- ^ Autti, S.; Heikkinen, P. J.; Mäkinen, J. T.; Volovik, G. E.; Zavjalov, V. V.; Eltsov, V. B. (February 2021). "AC Josephson effect between two superfluid time crystals". Nature Materials. 20 (2): 171–174. arXiv:2003.06313. Bibcode:2021NatMa..20..171A. doi:10.1038/s41563-020-0780-y. PMID 32807922. S2CID 212717702.
- ^ Träger, Nick; Gruszecki, Paweł; Lisiecki, Filip; Groß, Felix; Förster, Johannes; Weigand, Markus; Głowiński, Hubert; Kuświk, Piotr; Dubowik, Janusz; Schütz, Gisela; Krawczyk, Maciej (2021-02-03). "Real-Space Observation of Magnon Interaction with Driven Space–Time Crystals". Physical Review Letters. 126 (5): 057201. arXiv:1911.13192. Bibcode:2021PhRvL.126e7201T. doi:10.1103/PhysRevLett.126.057201. PMID 33605763. S2CID 208512720.
- ^ Williams, Jon (9 February 2021). "World's first video recording of a space–time crystal". Max Planck Institute for Intelligent Systems. Retrieved 2021-08-07.
- ^ Wolchover, Natalie (2021-07-30). "Eternal Change for No Energy: A Time Crystal Finally Made Real". Quanta Magazine. Retrieved 2021-07-30.
- ^ Kyprianidis, A.; Machado, F.; Morong, W.; Becker, P.; Collins, K. S.; Else, D. V.; Feng, L.; Hess, P. W.; Nayak, C.; Pagano, G.; Yao, N. Y. (2021-06-11). "Observation of a prethermal discrete time crystal". Science. 372 (6547): 1192–1196. arXiv:2102.01695. Bibcode:2021Sci...372.1192K. doi:10.1126/science.abg8102. ISSN 0036-8075. PMID 34112691. S2CID 231786633.
- ^ S, Robert; ers; Berkeley, U. C. (2021-11-10). "Creating Time Crystals Using New Quantum Computing Architectures". SciTechDaily. Retrieved 2021-12-27.
- ^ Randall, J.; Bradley, C. E.; van der Gronden, F. V.; Galicia, A.; Abobeih, M. H.; Markham, M.; Twitchen, D. J.; Machado, F.; Yao, N. Y.; Taminiau, T. H. (2021-12-17). "Many-body–localized discrete time crystal with a programmable spin-based quantum simulator". Science. 374 (6574): 1474–1478. arXiv:2107.00736. Bibcode:2021Sci...374.1474R. doi:10.1126/science.abk0603. ISSN 0036-8075. PMID 34735218. S2CID 235727352.
- ^ Boerkamp, Martijn (2021-11-17). "Physicists create discrete time crystals in a programmable quantum simulator". Physics World. Retrieved 2021-12-27.
- ^ Starr, Michelle (16 February 2022). "New Breakthrough Could Bring Time Crystals Out of The Lab And Into The Real World". ScienceAlert. Retrieved 2022-03-11.
- ^ Taheri, Hossein; Matsko, Andrey B.; Maleki, Lute; Sacha, Krzysztof (14 February 2022). "All-optical dissipative discrete time crystals". Nature Communications. 13 (1): 848. Bibcode:2022NatCo..13..848T. doi:10.1038/s41467-022-28462-x. ISSN 2041-1723. PMC 8844012. PMID 35165273.
- ^ Cho, Adrian (2022-03-02). "Physicists produce biggest time crystal yet". Science. doi:10.1126/science.adb1790.
- ^ Frey, Philipp; Rachel, Stephan (2022-03-04). "Realization of a discrete time crystal on 57 qubits of a quantum computer". Science Advances. 8 (9): eabm7652. arXiv:2105.06632. Bibcode:2022SciA....8M7652F. doi:10.1126/sciadv.abm7652. ISSN 2375-2548. PMC 8890700. PMID 35235347.
- ^ Frey, Philipp; Rachel, Stephan (2 March 2022). "'An ever-ticking clock': we made a 'time crystal' inside a quantum computer". The Conversation. Retrieved 2022-03-08.
Academic articles
[edit]- Boyle, Latham; Khoo, Jun Yong; Smith, Kendrick (2016). "Symmetric Satellite Swarms and Choreographic Crystals". Physical Review Letters. 116 (1): 015503. arXiv:1407.5876. Bibcode:2016PhRvL.116a5503B. doi:10.1103/PhysRevLett.116.015503. ISSN 0031-9007. PMID 26799028. S2CID 17918689.
- Bruno, Patrick (2013a). "Comment on 'Quantum Time Crystals'". Physical Review Letters. 110 (11): 118901. arXiv:1210.4128. Bibcode:2013PhRvL.110k8901B. doi:10.1103/PhysRevLett.110.118901. ISSN 0031-9007. PMID 25166585. S2CID 41459498.
- Bruno, Patrick (2013b). "Comment on "Space-Time Crystals of Trapped Ions"". Physical Review Letters. 111 (2): 029301. arXiv:1211.4792. Bibcode:2013PhRvL.111b9301B. doi:10.1103/PhysRevLett.111.029301. ISSN 0031-9007. PMID 23889455. S2CID 1502258.
- Else, Dominic V.; Bauer, Bela; Nayak, Chetan (2016). "Floquet Time Crystals". Physical Review Letters. 117 (9): 090402. arXiv:1603.08001. Bibcode:2016PhRvL.117i0402E. doi:10.1103/PhysRevLett.117.090402. ISSN 0031-9007. PMID 27610834. S2CID 1652633.
- Grifoni, Milena; Hänggi, Peter (1998). "Driven quantum tunneling" (PDF). Physics Reports. 304 (5–6): 229–354. Bibcode:1998PhR...304..229G. CiteSeerX 10.1.1.65.9479. doi:10.1016/S0370-1573(98)00022-2. ISSN 0370-1573. S2CID 120738031. Archived from the original (PDF) on 2017-02-11.
- Guo, Lingzhen; Marthaler, Michael; Schön, Gerd (2013). "Phase Space Crystals: A New Way to Create a Quasienergy Band Structure". Physical Review Letters. 111 (20): 205303. arXiv:1305.1800. Bibcode:2013PhRvL.111t5303G. doi:10.1103/PhysRevLett.111.205303. ISSN 0031-9007. PMID 24289695. S2CID 9337383.
- Guo, Lingzhen; Liang, Pengfei (2020). "Condensed matter physics in time crystals". New Journal of Physics. 22 (7): 075003. arXiv:2005.03138. Bibcode:2020NJPh...22g5003G. doi:10.1088/1367-2630/ab9d54. S2CID 218538401.
- Khemani, Vedika; Lazarides, Achilleas; Moessner, Roderich; Sondhi, S. L. (2016). "Phase Structure of Driven Quantum Systems". Physical Review Letters. 116 (25): 250401. arXiv:1508.03344. Bibcode:2016PhRvL.116y0401K. doi:10.1103/PhysRevLett.116.250401. ISSN 0031-9007. PMID 27391704. S2CID 883197.
- Li, Tongcang; Gong, Zhe-Xuan; Yin, Zhang-Qi; Quan, H. T.; Yin, Xiaobo; Zhang, Peng; Duan, L.-M.; Zhang, Xiang (2012a). "Space-Time Crystals of Trapped Ions". Physical Review Letters. 109 (16): 163001. arXiv:1206.4772. Bibcode:2012PhRvL.109p3001L. doi:10.1103/PhysRevLett.109.163001. ISSN 0031-9007. PMID 23215073. S2CID 8198228.
- Li, Tongcang; Gong, Zhe-Xuan; Yin, Zhang-Qi; Quan, H. T.; Yin, Xiaobo; Zhang, Peng; Duan, L.-M.; Zhang, Xiang (2012). "Reply to Comment on "Space–Time Crystals of Trapped Ions"". Unpublished. arXiv:1212.6959. Bibcode:2012arXiv1212.6959L.
- Lindner, Netanel H.; Refael, Gil; Galitski, Victor (2011). "Floquet topological insulator in semiconductor quantum wells". Nature Physics. 7 (6): 490–495. arXiv:1008.1792. Bibcode:2011NatPh...7..490L. doi:10.1038/nphys1926. ISSN 1745-2473. S2CID 26754031.
- Mendonça, J. T.; Dodonov, V. V. (2014). "Time Crystals in Ultracold Matter". Journal of Russian Laser Research. 35 (1): 93–100. doi:10.1007/s10946-014-9404-9. ISSN 1071-2836. S2CID 122631523.
- Nozières, Philippe (2013). "Time crystals: Can diamagnetic currents drive a charge density wave into rotation?". EPL. 103 (5): 57008. arXiv:1306.6229. Bibcode:2013EL....10357008N. doi:10.1209/0295-5075/103/57008. ISSN 0295-5075. S2CID 118662499.
- Robicheaux, F.; Niffenegger, K. (2015). "Quantum simulations of a freely rotating ring of ultracold and identical bosonic ions". Physical Review A. 91 (6): 063618. Bibcode:2015PhRvA..91f3618R. doi:10.1103/PhysRevA.91.063618. ISSN 2469-9926.
- Sacha, Krzysztof (2015). "Modeling spontaneous breaking of time-translation symmetry". Physical Review A. 91 (3): 033617. arXiv:1410.3638. Bibcode:2015PhRvA..91c3617S. doi:10.1103/PhysRevA.91.033617. ISSN 2469-9934. S2CID 118627872.
- Sacha, Krzysztof (2015). "Anderson localization and Mott insulator phase in the time domain". Scientific Reports. 5: 10787. arXiv:1502.02507. Bibcode:2015NatSR...510787S. doi:10.1038/srep10787. PMC 4466589. PMID 26074169.
- Sacha, Krzysztof; Zakrzewski, Jakub (2018). "Time Crystals: a review". Reports on Progress in Physics. 81 (1): 016401. arXiv:1704.03735. Bibcode:2018RPPh...81a6401S. doi:10.1088/1361-6633/aa8b38. PMID 28885193. S2CID 28224975.
- Shirley, Jon H. (1965). "Solution of the Schrödinger Equation with a Hamiltonian Periodic in Time". Physical Review. 138 (4B): B979–B987. Bibcode:1965PhRv..138..979S. doi:10.1103/PhysRev.138.B979. ISSN 0031-899X.
- Smith, J.; Lee, A.; Richerme, P.; Neyenhuis, B.; Hess, P. W.; Hauke, P.; Heyl, M.; Huse, D. A.; Monroe, C. (2016). "Many-body localization in a quantum simulator with programmable random disorder". Nature Physics. 12 (10): 907–911. arXiv:1508.07026. Bibcode:2016NatPh..12..907S. doi:10.1038/nphys3783. ISSN 1745-2473. S2CID 53408060.
- Volovik, G. E. (2013). "On the broken time translation symmetry in macroscopic systems: Precessing states and off-diagonal long-range order". JETP Letters. 98 (8): 491–495. arXiv:1309.1845. Bibcode:2013JETPL..98..491V. doi:10.1134/S0021364013210133. ISSN 0021-3640. S2CID 119100114.
- von Keyserlingk, C. W.; Khemani, Vedika; Sondhi, S. L. (2016). "Absolute stability and spatiotemporal long-range order in Floquet systems". Physical Review B. 94 (8): 085112. arXiv:1605.00639. Bibcode:2016PhRvB..94h5112V. doi:10.1103/PhysRevB.94.085112. ISSN 2469-9950. S2CID 118699328.
- Wang, Y. H.; Steinberg, H.; Jarillo-Herrero, P.; Gedik, N. (2013). "Observation of Floquet-Bloch States on the Surface of a Topological Insulator". Science. 342 (6157): 453–457. arXiv:1310.7563. Bibcode:2013Sci...342..453W. doi:10.1126/science.1239834. hdl:1721.1/88434. ISSN 0036-8075. PMID 24159040. S2CID 29121373.
- Wilczek, Frank (2013a). "Wilczek Reply" (PDF). Physical Review Letters. 110 (11): 118902. Bibcode:2013PhRvL.110k8902W. doi:10.1103/PhysRevLett.110.118902. ISSN 0031-9007. PMID 25166586.
- Wilczek, Frank (2013). "Superfluidity and Space–Time Translation Symmetry Breaking". Physical Review Letters. 111 (25): 250402. arXiv:1308.5949. Bibcode:2013PhRvL.111y0402W. doi:10.1103/PhysRevLett.111.250402. ISSN 0031-9007. PMID 24483732. S2CID 7537145.
- Yoshii, Ryosuke; Takada, Satoshi; Tsuchiya, Shunji; Marmorini, Giacomo; Hayakawa, Hisao; Nitta, Muneto (2015). "Fulde-Ferrell-Larkin-Ovchinnikov states in a superconducting ring with magnetic fields: Phase diagram and the first-order phase transitions". Physical Review B. 92 (22): 224512. arXiv:1404.3519. Bibcode:2015PhRvB..92v4512Y. doi:10.1103/PhysRevB.92.224512. ISSN 1098-0121. S2CID 118348062.
- Zel'Dovich, Y. B. (1967). "The quasienergy of a quantum-mechanical system subjected to a periodic action" (PDF). Soviet Physics JETP. 24 (5): 1006–1008. Bibcode:1967JETP...24.1006Z. Archived from the original (PDF) on 2017-02-11. Retrieved 2017-02-08.
Books
[edit]- Sacha, Krzysztof (2020). Time Crystals. Springer Series on Atomic, Optical, and Plasma Physics. Vol. 114. Springer. doi:10.1007/978-3-030-52523-1. ISBN 978-3-030-52522-4. S2CID 240770955.
Press
[edit]- Ball, Philip (20 September 2021). "Focus: Turning a Quantum Computer into a Time Crystal". Physics. 14. APS Physics: 131. doi:10.1103/Physics.14.131.
- Ball, Philip (8 January 2016). "Focus: New Crystal Type is Always in Motion". physics.aps.org. APS Physics. Archived from the original on 3 February 2017.
- Coleman, Piers (9 January 2013). "Quantum physics: Time crystals". Nature. 493 (7431): 166–167. Bibcode:2013Natur.493..166C. doi:10.1038/493166a. ISSN 0028-0836. PMID 23302852. S2CID 205075903.
- Cowen, Ron (27 February 2012). ""Time Crystals" Could Be a Legitimate Form of Perpetual Motion". scientificamerican.com. Scientific American. Archived from the original on 2 February 2017.
- Gibney, Elizabeth (2017). "The quest to crystallize time". Nature. 543 (7644): 164–166. Bibcode:2017Natur.543..164G. doi:10.1038/543164a. ISSN 0028-0836. PMID 28277535. S2CID 4460265.
- Grossman, Lisa (18 January 2012). "Death-defying time crystal could outlast the universe". newscientist.com. New Scientist. Archived from the original on 2 February 2017.
- Hackett, Jennifer (22 February 2016). "Curious Crystal Dances for Its Symmetry". scientificamerican.com. Scientific American. Archived from the original on 3 February 2017.
- Hannaford, Peter; Sacha, Krzysztof (17 Mar 2020). "Time crystals enter the real world of condensed matter". physicsworld.com. Institute of Physics.
- Hewitt, John (3 May 2013). "Creating time crystals with a rotating ion ring". phys.org. Science X. Archived from the original on 4 July 2013.
- Johnston, Hamish (18 January 2016). "'Choreographic crystals' have all the right moves". physicsworld.com. Institute of Physics. Archived from the original on 3 February 2017.
- Joint Quantum Institute (22 March 2011). "Floquet Topological Insulators". jqi.umd.edu. Joint Quantum Institute.
- Ouellette, Jennifer (31 January 2017). "World's first time crystals cooked up using new recipe". newscientist.com. New Scientist. Archived from the original on 1 February 2017.
- Powell, Devin (2013). "Can matter cycle through shapes eternally?". Nature. doi:10.1038/nature.2013.13657. ISSN 1476-4687. S2CID 181223762. Archived from the original on 3 February 2017.
- University of California, Berkeley (26 January 2017). "Physicists unveil new form of matter—time crystals". phys.org. Science X. Archived from the original on 28 January 2017.
- Weiner, Sophie (28 January 2017). "Scientists Create A New Kind Of Matter: Time Crystals". popularmechanics.com. Popular mechanics. Archived from the original on 3 February 2017.
- Wood, Charlie (31 January 2017). "Time crystals realize new order of space-time". csmonitor.com. Christian Science Monitor. Archived from the original on 2 February 2017.
- Yirka, Bob (9 July 2012). "Physics team proposes a way to create an actual space-time crystal". phys.org. Science X. Archived from the original on 15 April 2013.
- Zyga, Lisa (20 February 2012). "Time crystals could behave almost like perpetual motion machines". phys.org. Science X. Archived from the original on 3 February 2017.
- Zyga, Lisa (22 August 2013). "Physicist proves impossibility of quantum time crystals". phys.org. Space X. Archived from the original on 3 February 2017.
- Zyga, Lisa (9 July 2015). "Physicists propose new definition of time crystals—then prove such things don't exist". phys.org. Science X. Archived from the original on 9 July 2015.
- Zyga, Lisa (9 September 2016). "Time crystals might exist after all (Update)". phys.org. Science X. Archived from the original on 11 September 2016.