Systems biology
| Complex systems |
|---|
| Topics |

Systems biology is the computational and mathematical analysis and modeling of complex biological systems. It is a biology-based interdisciplinary field of study that focuses on complex interactions within biological systems, using a holistic approach (holism instead of the more traditional reductionism) to biological research.[1]
Particularly from the year 2000 onwards, the concept has been used widely in biology in a variety of contexts. The Human Genome Project is an example of applied systems thinking in biology which has led to new, collaborative ways of working on problems in the biological field of genetics.[2] One of the aims of systems biology is to model and discover emergent properties, properties of cells, tissues and organisms functioning as a system whose theoretical description is only possible using techniques of systems biology.[1][3] These typically involve metabolic networks or cell signaling networks.[1][4]
Overview
[edit]This section is written like a personal reflection, personal essay, or argumentative essay that states a Wikipedia editor's personal feelings or presents an original argument about a topic. (December 2022) |
Systems biology can be considered from a number of different aspects.
As a field of study, particularly, the study of the interactions between the components of biological systems, and how these interactions give rise to the function and behavior of that system (for example, the enzymes and metabolites in a metabolic pathway or the heart beats).[5][6][7]
As a paradigm, systems biology is usually defined in antithesis to the so-called reductionist paradigm (biological organisation), although it is consistent with the scientific method. The distinction between the two paradigms is referred to in these quotations: "the reductionist approach has successfully identified most of the components and many of the interactions but, unfortunately, offers no convincing concepts or methods to understand how system properties emerge ... the pluralism of causes and effects in biological networks is better addressed by observing, through quantitative measures, multiple components simultaneously and by rigorous data integration with mathematical models." (Sauer et al.)[8] "Systems biology ... is about putting together rather than taking apart, integration rather than reduction. It requires that we develop ways of thinking about integration that are as rigorous as our reductionist programmes, but different. ... It means changing our philosophy, in the full sense of the term." (Denis Noble)[7]
As a series of operational protocols used for performing research, namely a cycle composed of theory, analytic or computational modelling to propose specific testable hypotheses about a biological system, experimental validation, and then using the newly acquired quantitative description of cells or cell processes to refine the computational model or theory.[9] Since the objective is a model of the interactions in a system, the experimental techniques that most suit systems biology are those that are system-wide and attempt to be as complete as possible. Therefore, transcriptomics, metabolomics, proteomics and high-throughput techniques are used to collect quantitative data for the construction and validation of models.[10]
As the application of dynamical systems theory to molecular biology. Indeed, the focus on the dynamics of the studied systems is the main conceptual difference between systems biology and bioinformatics.[11]
As a socioscientific phenomenon defined by the strategy of pursuing integration of complex data about the interactions in biological systems from diverse experimental sources using interdisciplinary tools and personnel.[12]
History
[edit]Although the concept of a systems view of cellular function has been well understood since at least the 1930s,[13] technological limitations made it difficult to make systems wide measurements. The advent of microarray technology in the 1990s opened up an entire new visa for studying cells at the systems level. In 2000, the Institute for Systems Biology was established in Seattle in an effort to lure "computational" type people who it was felt were not attracted to the academic settings of the university. The institute did not have a clear definition of what the field actually was: roughly bringing together people from diverse fields to use computers to holistically study biology in new ways.[14] A Department of Systems Biology at Harvard Medical School was launched in 2003.[15] In 2006 it was predicted that the buzz generated by the "very fashionable" new concept would cause all the major universities to need a systems biology department, thus that there would be careers available for graduates with a modicum of ability in computer programming and biology.[14] In 2006 the National Science Foundation put forward a challenge to build a mathematical model of the whole cell.[citation needed] In 2012 the first whole-cell model of Mycoplasma genitalium was achieved by the Covert Laboratory at Stanford University. The whole-cell model is able to predict viability of M. genitalium cells in response to genetic mutations.[16]
An earlier precursor of systems biology, as a distinct discipline, may have been by systems theorist Mihajlo Mesarovic in 1966 with an international symposium at the Case Institute of Technology in Cleveland, Ohio, titled Systems Theory and Biology. Mesarovic predicted that perhaps in the future there would be such a thing as "systems biology".[17][18] Other early precursors that focused on the view that biology should be analyzed as a system, rather than a simple collection of parts, were Metabolic Control Analysis, developed by Henrik Kacser and Jim Burns[19] later thoroughly revised,[20] and Reinhart Heinrich and Tom Rapoport,[21] and Biochemical Systems Theory developed by Michael Savageau[22][23][24]
According to Robert Rosen in the 1960s, holistic biology had become passé by the early 20th century, as more empirical science dominated by molecular chemistry had become popular.[18] Echoing him forty years later in 2006 Kling writes that the success of molecular biology throughout the 20th century had suppressed holistic computational methods.[14] By 2011 the National Institutes of Health had made grant money available to support over ten systems biology centers in the United States,[25] but by 2012 Hunter writes that systems biology still has someway to go to achieve its full potential. Nonetheless, proponents hoped that it might once prove more useful in the future.[26]
An important milestone in the development of systems biology has become the international project Physiome.[citation needed]
Associated disciplines
[edit]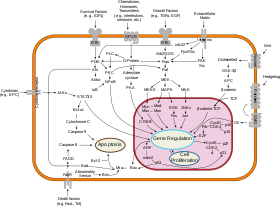
According to the interpretation of systems biology as using large data sets using interdisciplinary tools, a typical application is metabolomics, which is the complete set of all the metabolic products, metabolites, in the system at the organism, cell, or tissue level.[28]
Items that may be a computer database include: phenomics, organismal variation in phenotype as it changes during its life span; genomics, organismal deoxyribonucleic acid (DNA) sequence, including intra-organismal cell specific variation. (i.e., telomere length variation); epigenomics/epigenetics, organismal and corresponding cell specific transcriptomic regulating factors not empirically coded in the genomic sequence. (i.e., DNA methylation, Histone acetylation and deacetylation, etc.); transcriptomics, organismal, tissue or whole cell gene expression measurements by DNA microarrays or serial analysis of gene expression; interferomics, organismal, tissue, or cell-level transcript correcting factors (i.e., RNA interference), proteomics, organismal, tissue, or cell level measurements of proteins and peptides via two-dimensional gel electrophoresis, mass spectrometry or multi-dimensional protein identification techniques (advanced HPLC systems coupled with mass spectrometry). Sub disciplines include phosphoproteomics, glycoproteomics and other methods to detect chemically modified proteins; glycomics, organismal, tissue, or cell-level measurements of carbohydrates; lipidomics, organismal, tissue, or cell level measurements of lipids.[citation needed]
The molecular interactions within the cell are also studied, this is called interactomics.[29] A discipline in this field of study is protein–protein interactions, although interactomics includes the interactions of other molecules.[citation needed] Neuroelectrodynamics, where the computer's or a brain's computing function as a dynamic system is studied along with its (bio)physical mechanisms;[30] and fluxomics, measurements of the rates of metabolic reactions in a biological system (cell, tissue, or organism).[28]
In approaching a systems biology problem there are two main approaches. These are the top down and bottom up approach. The top down approach takes as much of the system into account as possible and relies largely on experimental results. The RNA-Seq technique is an example of an experimental top down approach. Conversely, the bottom up approach is used to create detailed models while also incorporating experimental data. An example of the bottom up approach is the use of circuit models to describe a simple gene network.[31]
Various technologies utilized to capture dynamic changes in mRNA, proteins, and post-translational modifications. Mechanobiology, forces and physical properties at all scales, their interplay with other regulatory mechanisms;[32] biosemiotics, analysis of the system of sign relations of an organism or other biosystems; Physiomics, a systematic study of physiome in biology.
Cancer systems biology is an example of the systems biology approach, which can be distinguished by the specific object of study (tumorigenesis and treatment of cancer). It works with the specific data (patient samples, high-throughput data with particular attention to characterizing cancer genome in patient tumour samples) and tools (immortalized cancer cell lines, mouse models of tumorigenesis, xenograft models, high-throughput sequencing methods, siRNA-based gene knocking down high-throughput screenings, computational modeling of the consequences of somatic mutations and genome instability).[33] The long-term objective of the systems biology of cancer is ability to better diagnose cancer, classify it and better predict the outcome of a suggested treatment, which is a basis for personalized cancer medicine and virtual cancer patient in more distant prospective. Significant efforts in computational systems biology of cancer have been made in creating realistic multi-scale in silico models of various tumours.[34]
The systems biology approach often involves the development of mechanistic models, such as the reconstruction of dynamic systems from the quantitative properties of their elementary building blocks.[35][36][37][38] For instance, a cellular network can be modelled mathematically using methods coming from chemical kinetics[39] and control theory. Due to the large number of parameters, variables and constraints in cellular networks, numerical and computational techniques are often used (e.g., flux balance analysis).[37][39]
Bioinformatics and data analysis
[edit]Other aspects of computer science, informatics, and statistics are also used in systems biology. These include new forms of computational models, such as the use of process calculi to model biological processes (notable approaches include stochastic π-calculus, BioAmbients, Beta Binders, BioPEPA, and Brane calculus) and constraint-based modeling; integration of information from the literature, using techniques of information extraction and text mining;[40] development of online databases and repositories for sharing data and models, approaches to database integration and software interoperability via loose coupling of software, websites and databases, or commercial suits; network-based approaches for analyzing high dimensional genomic data sets. For example, weighted correlation network analysis is often used for identifying clusters (referred to as modules), modeling the relationship between clusters, calculating fuzzy measures of cluster (module) membership, identifying intramodular hubs, and for studying cluster preservation in other data sets; pathway-based methods for omics data analysis, e.g. approaches to identify and score pathways with differential activity of their gene, protein, or metabolite members.[41] Much of the analysis of genomic data sets also include identifying correlations. Additionally, as much of the information comes from different fields, the development of syntactically and semantically sound ways of representing biological models is needed.[42]
Creating biological models
[edit]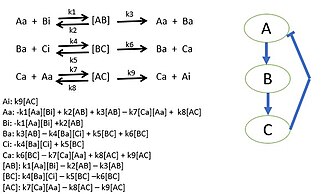
Researchers begin by choosing a biological pathway and diagramming all of the protein, gene, and/or metabolic pathways. After determining all of the interactions, mass action kinetics or enzyme kinetic rate laws are used to describe the speed of the reactions in the system. Using mass-conservation, the differential equations for the biological system can be constructed. Experiments or parameter fitting can be done to determine the parameter values to use in the differential equations.[44] These parameter values will be the various kinetic constants required to fully describe the model. This model determines the behavior of species in biological systems and bring new insight to the specific activities of system. Sometimes it is not possible to gather all reaction rates of a system. Unknown reaction rates are determined by simulating the model of known parameters and target behavior which provides possible parameter values.[45][43]
The use of constraint-based reconstruction and analysis (COBRA) methods has become popular among systems biologists to simulate and predict the metabolic phenotypes, using genome-scale models. One of the methods is the flux balance analysis (FBA) approach, by which one can study the biochemical networks and analyze the flow of metabolites through a particular metabolic network, by optimizing the objective function of interest (e.g. maximizing biomass production to predict growth).[46]

See also
[edit]- Biochemical systems equation
- Biological computation
- BioSystems (journal)
- Computational biology
- Exposome
- Interactome
- List of omics topics in biology
- List of systems biology modeling software
- Living systems
- Metabolic Control Analysis
- Metabolic network modelling
- Modelling biological systems
- Molecular pathological epidemiology
- Network biology
- Network medicine
- Synthetic biology
- Systems biomedicine
- Systems immunology
- Systems medicine
- TIARA (database)
References
[edit]- ^ a b c Tavassoly, Iman; Goldfarb, Joseph; Iyengar, Ravi (2018-10-04). "Systems biology primer: the basic methods and approaches". Essays in Biochemistry. 62 (4): 487–500. doi:10.1042/EBC20180003. ISSN 0071-1365. PMID 30287586. S2CID 52922135.
- ^ Zewail, Ahmed (2008). Physical Biology: From Atoms to Medicine. Imperial College Press. p. 339.
- ^ Longo, Giuseppe; Montévil, Maël (2014). Perspectives on Organisms - Springer. Lecture Notes in Morphogenesis. doi:10.1007/978-3-642-35938-5. ISBN 978-3-642-35937-8. S2CID 27653540.
- ^ Bu Z, Callaway DJ (2011). "Proteins MOVE! Protein dynamics and long-range allostery in cell signaling". Protein Structure and Diseases. Advances in Protein Chemistry and Structural Biology. Vol. 83. pp. 163–221. doi:10.1016/B978-0-12-381262-9.00005-7. ISBN 978-0-123-81262-9. PMID 21570668.
- ^ Snoep, Jacky L; Westerhoff, Hans V (2005). "From isolation to integration, a systems biology approach for building the Silicon Cell". In Alberghina, Lilia; Westerhoff, Hans V (eds.). Systems Biology: Definitions and Perspectives. Topics in Current Genetics. Vol. 13. Berlin: Springer-Verlag. pp. 13–30. doi:10.1007/b106456. ISBN 978-3-540-22968-1.
- ^ "Systems Biology: the 21st Century Science". Institute for Systems Biology. Retrieved 15 June 2011.
- ^ a b Noble, Denis (2006). The music of life: Biology beyond the genome. Oxford: Oxford University Press. p. 176. ISBN 978-0-19-929573-9.
- ^ Sauer, Uwe; Heinemann, Matthias; Zamboni, Nicola (27 April 2007). "Genetics: Getting Closer to the Whole Picture". Science. 316 (5824): 550–551. doi:10.1126/science.1142502. PMID 17463274. S2CID 42448991.
- ^ Kholodenko, Boris N; Sauro, Herbert M (2005). "Mechanistic and modular approaches to modeling and inference of cellular regulatory networks". In Alberghina, Lilia; Westerhoff, Hans V (eds.). Systems Biology: Definitions and Perspectives. Topics in Current Genetics. Vol. 13. Berlin: Springer-Verlag. pp. 357–451. doi:10.1007/b136809. ISBN 978-3-540-22968-1.
- ^ Chiara Romualdi; Gerolamo Lanfranchi (2009). "Statistical Tools for Gene Expression Analysis and Systems Biology and Related Web Resources". In Stephen Krawetz (ed.). Bioinformatics for Systems Biology (2nd ed.). Humana Press. pp. 181–205. doi:10.1007/978-1-59745-440-7_11. ISBN 978-1-59745-440-7.
- ^ Voit, Eberhard (2012). A First Course in Systems Biology. Garland Science. ISBN 9780815344674.
- ^ Baitaluk, M. (2009). "System Biology of Gene Regulation". Biomedical Informatics. Methods in Molecular Biology. Vol. 569. pp. 55–87. doi:10.1007/978-1-59745-524-4_4. ISBN 978-1-934115-63-3. PMID 19623486.
- ^ Wright, Sewall (1934). "Physiological and Evolutionary Theories of Dominance". The American Naturalist. pp. 24–53.
- ^ a b c Kling, Jim (3 March 2006). "Working the Systems". Science. Retrieved 15 June 2011.
- ^ "HMS launches new department to study systems biology". Harvard Gazette. September 23, 2003.
- ^ Karr, Jonathan R.; Sanghvi, Jayodita C.; Macklin, Derek N.; Gutschow, Miriam V.; Jacobs, Jared M.; Bolival, Benjamin; Assad-Garcia, Nacyra; Glass, John I.; Covert, Markus W. (July 2012). "A Whole-Cell Computational Model Predicts Phenotype from Genotype". Cell. 150 (2): 389–401. doi:10.1016/j.cell.2012.05.044. PMC 3413483. PMID 22817898.
- ^ Mesarovic, Mihajlo D. (1968). Systems Theory and Biology. Berlin: Springer-Verlag.
- ^ a b Rosen, Robert (5 July 1968). "A Means Toward a New Holism". Science. 161 (3836): 34–35. Bibcode:1968Sci...161...34M. doi:10.1126/science.161.3836.34. JSTOR 1724368.
- ^ Kacser, H; Burns, JA (1973). "The control of flux". Symposia of the Society for Experimental Biology. 27: 65–104. PMID 4148886.
- ^ Kacser, H; Burns, JA; Fell, DA (1995). "The control of flux". Biochemical Society Transactions. 23 (2): 341–366. doi:10.1042/bst0230341. PMID 7672373.
- ^ Heinrich, R; Rapoport, TA (1974). "A linear steady-state theory of enzymatic chains: general properties, control and effector strength". European Journal of Biochemistry. 42 (1): 89–95. doi:10.1111/j.1432-1033.1974.tb03318.x. PMID 4830198.
- ^ Savageau, Michael A. (December 1969). "Journal of Theoretical Biology". 25 (3): 365–369. doi:10.1016/S0022-5193(69)80026-3. PMID 5387046.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Savageau, Michael A. (December 1969). "Journal of Theoretical Biology". 25 (3): 370–379. doi:10.1016/S0022-5193(69)80027-5. PMID 5387047.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Savageau, Michael A. (February 1970). "Journal of Theoretical Biology". 26 (2): 215–226. doi:10.1016/S0022-5193(70)80013-3. PMID 5434343.
{{cite journal}}: Cite journal requires|journal=(help) - ^ "Systems Biology - National Institute of General Medical Sciences". Archived from the original on 19 October 2013. Retrieved 12 December 2012.
- ^ Hunter, Philip (May 2012). "Back down to Earth: Even if it has not yet lived up to its promises, systems biology has now matured and is about to deliver its first results". EMBO Reports. 13 (5): 408–411. doi:10.1038/embor.2012.49. PMC 3343359. PMID 22491028.
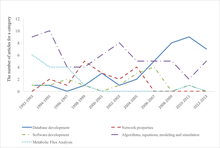
- ^ Zou, Yawen; Laubichler, Manfred D. (2018-07-25). "From systems to biology: A computational analysis of the research articles on systems biology from 1992 to 2013". PLOS ONE. 13 (7): e0200929. Bibcode:2018PLoSO..1300929Z. doi:10.1371/journal.pone.0200929. ISSN 1932-6203. PMC 6059489. PMID 30044828.
- ^ a b Cascante, Marta; Marin, Silvia (2008-09-30). "Metabolomics and fluxomics approaches". Essays in Biochemistry. 45: 67–82. doi:10.1042/bse0450067. ISSN 0071-1365. PMID 18793124.
- ^ Cusick, Michael E.; Klitgord, Niels; Vidal, Marc; Hill, David E. (2005-10-15). "Interactome: gateway into systems biology". Human Molecular Genetics. 14 (suppl_2): R171–R181. doi:10.1093/hmg/ddi335. ISSN 0964-6906. PMID 16162640.
- ^ Aur, Dorian (2012). "From Neuroelectrodynamics to Thinking Machines". Cognitive Computation. 4 (1): 4–12. doi:10.1007/s12559-011-9106-3. ISSN 1866-9956. S2CID 12355069.
- ^ Loor, Khuram Shahzad and Juan J. (2012-07-31). "Application of Top-Down and Bottom-up Systems Approaches in Ruminant Physiology and Metabolism". Current Genomics. 13 (5): 379–394. doi:10.2174/138920212801619269. PMC 3401895. PMID 23372424.
- ^ Spill, Fabian; Bakal, Chris; Mak, Michael (2018). "Mechanical and Systems Biology of Cancer". Computational and Structural Biotechnology Journal. 16: 237–245. arXiv:1807.08990. Bibcode:2018arXiv180708990S. doi:10.1016/j.csbj.2018.07.002. PMC 6077126. PMID 30105089.
- ^ Barillot, Emmanuel; Calzone, Laurence; Hupe, Philippe; Vert, Jean-Philippe; Zinovyev, Andrei (2012). Computational Systems Biology of Cancer. Chapman & Hall/CRCMathematical & Computational Biology. p. 461. ISBN 978-1439831441.
- ^ Byrne, Helen M. (2010). "Dissecting cancer through mathematics: from the cell to the animal model". Nature Reviews Cancer. 10 (3): 221–230. doi:10.1038/nrc2808. PMID 20179714. S2CID 24616792.
- ^ Gardner, Timothy .S; di Bernardo, Diego; Lorenz, David; Collins, James J. (4 July 2003). "Inferring Genetic Networks and Identifying Compound Mode of Action via Expression Profiling". Science. 301 (5629): 102–105. Bibcode:2003Sci...301..102G. doi:10.1126/science.1081900. PMID 12843395. S2CID 8356492.
- ^ di Bernardo, Diego; Thompson, Michael J.; Gardner, Timothy S.; Chobot, Sarah E.; Eastwood, Erin L.; Wojtovich, Andrew P.; Elliott, Sean J.; Schaus, Scott E.; Collins, James J. (March 2005). "Chemogenomic profiling on a genome-wide scale using reverse-engineered gene networks". Nature Biotechnology. 23 (3): 377–383. doi:10.1038/nbt1075. PMID 15765094. S2CID 16270018.
- ^ a b Tavassoly, Iman (2015). Dynamics of Cell Fate Decision Mediated by the Interplay of Autophagy and Apoptosis in Cancer Cells. Springer Theses. Springer International Publishing. doi:10.1007/978-3-319-14962-2. ISBN 978-3-319-14961-5. S2CID 89307028.
- ^ Korkut, A; Wang, W; Demir, E; Aksoy, BA; Jing, X; Molinelli, EJ; Babur, Ö; Bemis, DL; Onur Sumer, S; Solit, DB; Pratilas, CA; Sander, C (18 August 2015). "Perturbation biology nominates upstream-downstream drug combinations in RAF inhibitor resistant melanoma cells". eLife. 4. doi:10.7554/eLife.04640. PMC 4539601. PMID 26284497.
- ^ a b Gupta, Ankur; Rawlings, James B. (April 2014). "Comparison of Parameter Estimation Methods in Stochastic Chemical Kinetic Models: Examples in Systems Biology". AIChE Journal. 60 (4): 1253–1268. doi:10.1002/aic.14409. ISSN 0001-1541. PMC 4946376. PMID 27429455.
- ^ Ananadou, Sophia; Kell, Douglas; Tsujii, Jun-ichi (December 2006). "Text mining and its potential applications in systems biology". Trends in Biotechnology. 24 (12): 571–579. doi:10.1016/j.tibtech.2006.10.002. PMID 17045684.
- ^ Glaab, Enrico; Schneider, Reinhard (2012). "PathVar: analysis of gene and protein expression variance in cellular pathways using microarray data". Bioinformatics. 28 (3): 446–447. doi:10.1093/bioinformatics/btr656. PMC 3268235. PMID 22123829.
- ^ Bardini, R.; Politano, G.; Benso, A.; Di Carlo, S. (2017-01-01). "Multi-level and hybrid modelling approaches for systems biology". Computational and Structural Biotechnology Journal. 15: 396–402. doi:10.1016/j.csbj.2017.07.005. ISSN 2001-0370. PMC 5565741. PMID 28855977.
- ^ a b Transtrum, Mark K.; Qiu, Peng (2016-05-17). "Bridging Mechanistic and Phenomenological Models of Complex Biological Systems". PLOS Computational Biology. 12 (5): e1004915. arXiv:1509.06278. Bibcode:2016PLSCB..12E4915T. doi:10.1371/journal.pcbi.1004915. ISSN 1553-7358. PMC 4871498. PMID 27187545.
- ^ Chellaboina, V.; Bhat, S. P.; Haddad, W. M.; Bernstein, D. S. (August 2009). "Modeling and analysis of mass-action kinetics". IEEE Control Systems Magazine. 29 (4): 60–78. doi:10.1109/MCS.2009.932926. ISSN 1941-000X. S2CID 12122032.
- ^ Brown, Kevin S.; Sethna, James P. (2003-08-12). "Statistical mechanical approaches to models with many poorly known parameters". Physical Review E. 68 (2): 021904. Bibcode:2003PhRvE..68b1904B. doi:10.1103/physreve.68.021904. ISSN 1063-651X. PMID 14525003.
- ^ Orth, Jeffrey D; Thiele, Ines; Palsson, Bernhard Ø (March 2010). "What is flux balance analysis?". Nature Biotechnology. 28 (3): 245–248. doi:10.1038/nbt.1614. ISSN 1087-0156. PMC 3108565. PMID 20212490.
Further reading
[edit]- Klipp, Edda; Liebermeister, Wolfram; Wierling, Christoph; Kowald, Axel (2016). Systems Biology - A Textbook, 2nd edition. Wiley. ISBN 978-3-527-33636-4.
- Asfar S. Azmi, ed. (2012). Systems Biology in Cancer Research and Drug Discovery. Springer. ISBN 978-94-007-4819-4.
- Kitano, Hiroaki (15 October 2001). Foundations of Systems Biology. MIT Press. ISBN 978-0-262-11266-6.
- Werner, Eric (29 March 2007). "All systems go". Nature. 446 (7135): 493–494. Bibcode:2007Natur.446..493W. doi:10.1038/446493a. provides a comparative review of three books:
- Alon, Uri (7 July 2006). An Introduction to Systems Biology: Design Principles of Biological Circuits. Chapman & Hall. ISBN 978-1-58488-642-6.
- Kaneko, Kunihiko (15 September 2006). Life: An Introduction to Complex Systems Biology. Springer-Verlag. Bibcode:2006lics.book.....K. ISBN 978-3-540-32666-3.
- Palsson, Bernhard O. (16 January 2006). Systems Biology: Properties of Reconstructed Networks. Cambridge University Press. ISBN 978-0-521-85903-5.
- Werner Dubitzky; Olaf Wolkenhauer; Hiroki Yokota; Kwan-Hyun Cho, eds. (13 August 2013). Encyclopedia of Systems Biology. Springer-Verlag. ISBN 978-1-4419-9864-4.
External links
[edit] Media related to Systems biology at Wikimedia Commons
Media related to Systems biology at Wikimedia Commons- Biological Systems in bio-physics-wiki

