Ancient Greek astronomy

The Antikythera Mechanism was an analog computer from 150–100 BC designed to calculate the positions of astronomical objects.

Greek astronomy is astronomy written in the Greek language in classical antiquity. Greek astronomy is understood to include the ancient Greek, Hellenistic, Greco-Roman, and Late Antiquity eras. It is not limited geographically to Greece or to ethnic Greeks, as the Greek language had become the language of scholarship throughout the Hellenistic world following the conquests of Alexander. This phase of Greek astronomy is also known as Hellenistic astronomy, while the pre-Hellenistic phase is known as Classical Greek astronomy. During the Hellenistic and Roman periods, much of the Greek and non-Greek astronomers working in the Greek tradition studied at the Musaeum and the Library of Alexandria in Ptolemaic Egypt.

The development of astronomy by the Greek and notably Hellenistic astronomers is considered to be a major phase in the history of astronomy. Greek astronomy is characterized by seeking a geometrical model for celestial phenomena. Most of the names of the stars, planets, and constellations of the northern hemisphere are inherited from the terminology of the Greek astronomy, which are however indeed transliterated from the empirical knowledge in Babylonian astronomy, characterized by its theoretical model formulation in terms of algebraic and numerical relations, and to a lesser extent from Egyptian astronomy. Later, the scientific work by astronomers and mathematicians of the arbo-moslem empire, of diverse backgrounds and religions (such as the Syriac Christians), to translate, comment and then correct Ptolemy's Almagest, influenced in their turn Indian and Western European astronomy.

Archaic Greek astronomy

Both Hesiod and Homer were directly and deeply influenced by the mythologies of Phoenicia and Mesopotamia, thanks to Phoenician sailors and literate Babylonians and Arameans who went to Lefkandi in Greece during the Orientalizing Period, between c. 750 BC and c. 630 BC, for maritime commerce and some to live and work; the Babylonians and Arameans came from the Levant and North Syria where they were forcibly transported in their hundreds of thousands by the Assyrian army from Babylonia during the reign of the last six Assyrian kings, from 745 BC to 627 BC. Hesiod's theogony and cosmogony are the Greek version of two Phoenician myths. The Odyssey of Homer is inspired by the Epopee of Gilgamesh. See for references the work of M.L. West et W. Burkret.

In this context it is reasonable to suggest that whatever Homer and Hesiod hinted at in their small contributions comes from the knowledge they acquired from the Oriental people they rubbed shoulder with in Lefkandi, the center of Greek culture at that time. References to identifiable stars and constellations appear in the writings of Homer and Hesiod, the earliest surviving examples of Greek literature. In the oldest European texts, the Iliad and the Odyssey, Homer has several astronomical phenomena including solar eclipses. In the Iliad and the Odyssey, Homer refers to the following celestial objects:

• the constellation Boötes
• the star cluster Hyades
• the constellation Orion
• the star cluster Pleiades
• Sirius, the Dog Star
• the constellation Ursa Major

Anaximander

We really have no material evidence whatever of what some Greek philosophers said or did between 600 BC and 300 BC. Despite this, continues the speculation that Anaximander (c. 610 BC–c. 546 BC) described a cyclical earth suspended in the center of the cosmos, surrounded by rings of fire, that Philolaus (c. 480 BC–c. 405 BC) the Pythagorean described a cosmos with the stars, planets, Sun, Moon, Earth, and a counter-Earth (Antichthon)—ten bodies in all—circling an unseen central fire. It is hence pure conjecture that Greeks of the 6th and 5th centuries BC were aware of the planets and speculated about the structure of the cosmos. Also, a more detailed description about the cosmos, Stars, Sun, Moon and the Earth can be found in the Orphism, which dates back to the end of the 5th century BC. Within the lyrics of the Orphic poems we can find remarkable information such as that the Earth is round, it has an axis and it moves around it in one day, it has three climate zones and that the Sun magnetizes the Stars and planets.

The Planets in Early Greek Astronomy

The name "planet" comes from the Greek term πλανήτης (planētēs), meaning "wanderer", as ancient astronomers noted how certain lights moved across the sky in relation to the other stars. Five extraterrestrial planets can be seen with the naked eye: Mercury, Venus, Mars, Jupiter, and Saturn, the Greek names being Hermes, Aphrodite, Ares, Zeus and Cronus. Sometimes the luminaries, the Sun and Moon, are added to the list of naked eye planets to make a total of seven. Since the planets disappear from time to time when they approach the Sun, careful attention is required to identify all five. Observations of Venus are not straightforward. Early Greeks thought that the evening and morning appearances of Venus represented two different objects, calling it Hesperus ("evening star") when it appeared in the western evening sky and Phosphorus ("light-bringer") when it appeared in the eastern morning sky. They eventually came to recognize that both objects were the same planet. Pythagoras is given credit for this realization.

Eudoxan astronomy

In classical Greece, astronomy was a branch of mathematics; astronomers sought to create geometrical models that could imitate the appearances of celestial motions. This tradition began with the Pythagoreans, who placed astronomy among the four mathematical arts (along with arithmetic, geometry, and music). The study of number comprising the four arts was later called the Quadrivium.

Although he was not a creative mathematician, Plato (427–347 BC) included the quadrivium as the basis for philosophical education in the Republic. He encouraged a younger mathematician, Eudoxus of Cnidus (c. 410 BC–c. 347 BC), to develop a system of Greek astronomy. According to a modern historian of science, David Lindberg:

"In their work we find (1) a shift from stellar to planetary concerns, (2) the creation of a geometrical model, the "two-sphere model," for the representation of stellar and planetary phenomena, and (3) the establishment of criteria governing theories designed to account for planetary observations".

The two-sphere model is a geocentric model that divides the cosmos into two regions, a spherical Earth, central and motionless (the sublunary sphere) and a spherical heavenly realm centered on the Earth, which may contain multiple rotating spheres made of aether.

Renaissance woodcut illustrating the two-sphere model.

Plato's main books on cosmology are the Timaeus and the Republic. In them he described the two-sphere model and said there were eight circles or spheres carrying the seven planets and the fixed stars. According to the "Myth of Er" in the Republic, the cosmos is the Spindle of Necessity, attended by Sirens and spun by the three daughters of the Goddess Necessity known collectively as the Moirai or Fates.

According to a story reported by Simplicius of Cilicia (6th century), Plato posed a question for the Greek mathematicians of his day: "By the assumption of what uniform and orderly motions can the apparent motions of the planets be accounted for?" (quoted in Lloyd 1970, p. 84). Plato proposed that the seemingly chaotic wandering motions of the planets could be explained by combinations of uniform circular motions centered on a spherical Earth, apparently a novel idea in the 4th century.

Eudoxus rose to the challenge by assigning to each planet a set of concentric spheres. By tilting the axes of the spheres, and by assigning each a different period of revolution, he was able to approximate the celestial "appearances." Thus, he was the first to attempt a mathematical description of the motions of the planets. A general idea of the content of On Speeds, his book on the planets, can be gleaned from Aristotle's Metaphysics XII, 8, and a commentary by Simplicius on De caelo, another work by Aristotle. Since all his own works are lost, our knowledge of Eudoxus is obtained from secondary sources. Aratus's poem on astronomy is based on a work of Eudoxus, and possibly also Theodosius of Bithynia's Sphaerics. They give us an indication of his work in spherical astronomy as well as planetary motions.

Callippus, a Greek astronomer of the 4th century, added seven spheres to Eudoxus' original 27 (in addition to the planetary spheres, Eudoxus included a sphere for the fixed stars). Aristotle described both systems, but insisted on adding "unrolling" spheres between each set of spheres to cancel the motions of the outer set. Aristotle was concerned about the physical nature of the system; without unrollers, the outer motions would be transferred to the inner planets.

Hellenistic astronomy

Planetary models and observational astronomy

The Eudoxan system had several critical flaws. One was its inability to predict motions exactly. Callippus' work may have been an attempt to correct this flaw. A related problem is the inability of his models to explain why planets appear to change speed. A third flaw is its inability to explain changes in the brightness of planets as seen from Earth. Because the spheres are concentric, planets will always remain at the same distance from Earth. This problem was pointed out in Antiquity by Autolycus of Pitane (c. 310 BC).

Apollonius of Perga (c. 262 BC–c. 190 BC) responded by introducing two new mechanisms that allowed a planet to vary its distance and speed: the eccentric deferent and the deferent and epicycle. The deferent is a circle carrying the planet around the Earth. (The word deferent comes from the Greek fero φέρω "to carry"and Latin ferro, ferre, meaning "to carry.") An eccentric deferent is slightly off-center from Earth. In a deferent and epicycle model, the deferent carries a small circle, the epicycle, which carries the planet. The deferent-and-epicycle model can mimic the eccentric model, as shown by Apollonius' theorem. It can also explain retrogradation, which happens when planets appear to reverse their motion through the zodiac for a short time. Modern historians of astronomy have determined that Eudoxus' models could only have approximated retrogradation crudely for some planets, and not at all for others.

In the 2nd century BC, Hipparchus, aware of the extraordinary accuracy with which Babylonian astronomers could predict the planets' motions, insisted that Greek astronomers achieve similar levels of accuracy. Somehow he had access to Babylonian observations or predictions, and used them to create better geometrical models. For the Sun, he used a simple eccentric model, based on observations of the equinoxes, which explained both changes in the speed of the Sun and differences in the lengths of the seasons. For the Moon, he used a deferent and epicycle model. He could not create accurate models for the remaining planets, and criticized other Greek astronomers for creating inaccurate models.

Hipparchus also compiled a star catalogue. According to Pliny the Elder, he observed a nova (new star). So that later generations could tell whether other stars came to be, perished, moved, or changed in brightness, he recorded the position and brightness of the stars. Ptolemy mentioned the catalogue in connection with Hipparchus' discovery of precession. (Precession of the equinoxes is a slow motion of the place of the equinoxes through the zodiac, caused by the shifting of the Earth's axis). Hipparchus thought it was caused by the motion of the sphere of fixed stars.

Heliocentrism and cosmic scales

Aristarchus's 3rd-century BCE calculations on the relative sizes of (from left) the Sun, Earth and Moon, from a 10th-century CE Greek copy

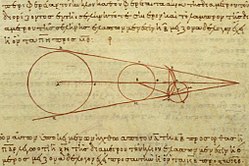
In the 3rd century BC, Aristarchus of Samos proposed an alternate cosmology (arrangement of the universe): a heliocentric model of the Solar System, placing the Sun, not the Earth, at the center of the known universe (hence he is sometimes known as the "Greek Copernicus"). His astronomical ideas were not well-received, however, and only a few brief references to them are preserved. We know the name of one follower of Aristarchus: Seleucus of Seleucia.

Aristarchus also wrote a book On the Sizes and Distances of the Sun and Moon, which is his only work to have survived. In this work, he calculated the sizes of the Sun and Moon, as well as their distances from the Earth in Earth radii. Shortly afterwards, Eratosthenes calculated the size of the Earth, providing a value for the Earth radii which could be plugged into Aristarchus' calculations. Hipparchus wrote another book On the Sizes and Distances of the Sun and Moon, which has not survived. Both Aristarchus and Hipparchus drastically underestimated the distance of the Sun from the Earth.

Astronomy in the Greco-Roman and Late Antique eras

Hipparchus is considered to have been among the most important Greek astronomers, because he introduced the concept of exact prediction into astronomy. He was also the last innovative astronomer before Claudius Ptolemy, a mathematician who worked at Alexandria in Roman Egypt in the 2nd century. Ptolemy's works on astronomy and astrology include the Almagest, the Planetary Hypotheses, and the Tetrabiblos, as well as the Handy Tables, the Canobic Inscription, and other minor works.

Ptolemaic astronomy

The Almagest is one of the most influential books in the history of Western astronomy. In this book, Ptolemy explained how to predict the behavior of the planets, as Hipparchus could not, with the introduction of a new mathematical tool, the equant. The Almagest gave a comprehensive treatment of astronomy, incorporating theorems, models, and observations from many previous mathematicians. This fact may explain its survival, in contrast to more specialized works that were neglected and lost. Ptolemy placed the planets in the order that would remain standard until it was displaced by the heliocentric system and the Tychonic system:

1. Moon
2. Mercury
3. Venus
4. Sun
5. Mars
6. Jupiter
7. Saturn
8. Fixed stars

The extent of Ptolemy's reliance on the work of other mathematicians, in particular his use of Hipparchus' star catalogue, has been debated since the 19th century. A controversial claim was made by Robert R. Newton in the 1970s. in The Crime of Claudius Ptolemy, he argued that Ptolemy faked his observations and falsely claimed the catalogue of Hipparchus as his own work. Newton's theories have not been adopted by most historians of astronomy.

Claudius Ptolemy of Alexandria performed a deep examination of the shape and motion of the Earth and celestial bodies. He worked at the museum, or instructional center, school and library of manuscripts in Alexandria. Ptolemy is responsible for a lot of concepts, but one of his most famous works summarizing these concepts is the Almagest, a series of 13 books where he presented his astronomical theories. Ptolemy discussed the idea of epicycles and center of the world. The epicycle center moves at a constant rate in a counter clockwise direction. Once other celestial bodies, such as the planets, were introduced into this system, it became more complex. The models for Jupiter, Saturn, and Mars included the center of the circle, the equant point, the epicycle, and an observer from earth to give perspective. The discovery of this model was that the center of the Mercury and Venus epicycles must always be colinear with the Sun. This assures of bounded elongation. (Bowler, 2010, 48) Bounded elongation is the angular distance of celestial bodies from the center of the universe. Ptolemy's model of the cosmos and his studies landed him an important place in history in the development of modern-day science. The cosmos was a concept further developed by Ptolemy that included equant circles, however Copernicus model of the universe was simpler. In the Ptolemaic system, the Earth was at the center of the universe with the Moon, the Sun, and five planets circling it. The circle of fixed stars marked the outermost sphere of the universe and beyond that would be the philosophical “aether” realm. The Earth was at the exact center of the cosmos, most likely because people at the time believed the Earth had to be at the center of the universe because of the deductions made by observers in the system. The sphere carrying the Moon is described as the boundary between the corruptible and changing sublunary world and the incorruptible and unchanging heavens above it (Bowler, 2010, 26). The heavens were defined as incorruptible and unchanging based on theology and mythology of the past. The Almagest introduced the idea of the sphericity of heavens. The assumption is that the sizes and mutual distances of the stars must appear to vary however one supposes the earth to be positioned, yet no such variation occurred (Bowler, 2010, 55), The aether is the area that describes the universe above the terrestrial sphere. This component of the atmosphere is unknown and named by philosophers, though many do not know what lies beyond the realm of what has been seen by human beings. The aether is used to affirm the sphericity of the heavens and this is confirmed by the belief that different shapes have an equal boundary and those with more angles are greater, the circle is greater than all other surfaces, and a sphere greater than all other solids. Therefore, through physical considerations, and heavenly philosophy, there is an assumption that the heavens must be spherical. The Almagest also suggested that the earth was spherical because of similar philosophy. The differences in the hours across the globe are proportional to the distances between the spaces at which they are being observed. Therefore, it can be deduced that the Earth is spherical because of the evenly curving surface and the differences in time that was constant and proportional. In other words, the Earth must be spherical because they change in time-zones across the world occur in a uniform fashion, as with the rotation of a sphere. The observation of eclipses further confirmed these findings because everyone on Earth could see a lunar eclipse, for example, but it would be at different hours. The Almagest also suggest that the Earth is at the center of the universe. The basis on which this is found is in the fact that six zodiac signs can be seen above Earth, while at the same time the other signs are not visible (Bowler, 2010, 57). The way that we observe the increase and decrease of daylight would be different if the Earth was not at the center of the universe. Though this view later proofed to be invalid, this was a good proponent to the discussion of the design of the universe. Ideas on the universe were later developed and advanced through the works of other philosophers such as Copernicus, who built on ideas through his knowledge of the world and God.

A few mathematicians of Late Antiquity wrote commentaries on the Almagest, including Pappus of Alexandria as well as Theon of Alexandria and his daughter Hypatia. Ptolemaic astronomy became standard in medieval western European and Islamic astronomy until it was displaced by Maraghan, heliocentric and Tychonic systems by the 16th century. However, recently discovered manuscripts reveal that Greek astrologers of Antiquity continued using pre-Ptolemaic methods for their calculations (Aaboe, 2001).

Influence on Indian astronomy

Further information: Indian astronomy

Greek equatorial sun dial, Ai-Khanoum, Afghanistan 3rd-2nd century BC.

Hellenistic astronomy is known to have been practiced near India in the Greco-Bactrian city of Ai-Khanoum from the 3rd century BC. Various sun-dials, including an equatorial sundial adjusted to the latitude of Ujjain have been found in archaeological excavations there. Numerous interactions with the Mauryan Empire, and the later expansion of the Indo-Greeks into India suggest that some transmission may have happened during that period.

Several Greco-Roman astrological treatises are also known to have been imported into India during the first few centuries of our era. The Yavanajataka ("Sayings of the Greeks") was translated from Greek to Sanskrit by Yavanesvara during the 2nd century, under the patronage of the Western Satrap Saka king Rudradaman I. Rudradaman's capital at Ujjain "became the Greenwich of Indian astronomers and the Arin of the Arabic and Latin astronomical treatises; for it was he and his successors who encouraged the introduction of Greek horoscopy and astronomy into India."

Later in the 6th century, the Romaka Siddhanta ("Doctrine of the Romans"), and the Paulisa Siddhanta (sometimes attributed as the "Doctrine of Paul" or in general the Doctrine of Paulisa muni) were considered as two of the five main astrological treatises, which were compiled by Varahamihira in his Pañca-siddhāntikā ("Five Treatises"). Varahamihira wrote in the Brihat-Samhita: "For, the Greeks are foreigners. This science is well established among them. Although they are revered as sages, how much more so is a twice-born person who knows the astral science."

Sources for Greek astronomy

Many Greek astronomical texts are known only by name, and perhaps by a description or quotations. Some elementary works have survived because they were largely non-mathematical and suitable for use in schools. Books in this class include the Phaenomena of Euclid and two works by Autolycus of Pitane. Three important textbooks, written shortly before Ptolemy's time, were written by Cleomedes, Geminus, and Theon of Smyrna. Books by Roman authors like Pliny the Elder and Vitruvius contain some information on Greek astronomy. The most important primary source is the Almagest, since Ptolemy refers to the work of many of his predecessors (Evans 1998, p. 24).

Famous astronomers of antiquity

In addition to the authors named in the article, the following list of people who worked on mathematical astronomy or cosmology may be of interest.

• Aglaonice
• Anaxagoras
• Archimedes
• Archytas
• Aristaeus
• Aristarchus
• Aristyllus
• Conon of Samos
• Democritus
• Empedocles
• Heraclides Ponticus
• Hicetas
• Hippocrates of Chios
• Macrobius
• Martianus Capella
• Menelaus of Alexandria (Menelaus theorem)
• Meton of Athens
• Parmenides
• Porphyry
• Posidonius
• Proclus
• Thales
• Theodosius of Bithynia

See also

• Antikythera mechanism
• Greek mathematics
• History of astronomy
• Babylonian influence on Greek astronomy

References

• Aaboe, Asger H. (2001). Episodes from the Early History of Astronomy. New York: Springer. ISBN 978-0-387-95136-2. {{cite book}}: Invalid |ref=harv (help)
• Dreyer, John L. E. (1953). A History of Astronomy from Thales to Kepler (2nd ed.). New York: Dover Publications. ISBN 978-0-486-60079-6. {{cite book}}: Invalid |ref=harv (help)
• Evans, James (1998). The History and Practice of Ancient Astronomy. New York: Oxford University Press. ISBN 978-0-19-509539-5. {{cite book}}: Invalid |ref=harv (help)
• Heath, Thomas L. (1913). Aristarchus of Samos. Oxford: Clarendon Press. {{cite book}}: Invalid |ref=harv (help)
• Lindberg, David C. (2010). The Beginnings of Western Science: The European Scientific Tradition in Philosophical, Religious, and Institutional Context, 600 B.C. to A.D. 1450 (2 ed.). Chicago: University of Chicago Press. ISBN 978-0-226-48204-0. {{cite book}}: Invalid |ref=harv (help)
• Lloyd, Geoffrey E. R. (1970). Early Greek Science: Thales to Aristotle. New York: W. W. Norton & Co. {{cite book}}: Invalid |ref=harv (help)
• Neugebauer, Otto E. (1975). A History of Ancient Mathematical Astronomy. Berlin: Springer. ISBN 978-0-387-06995-1. {{cite book}}: Invalid |ref=harv (help)
• Newton, Robert R. (1977). The Crime of Claudius Ptolemy. Baltimore: Johns Hopkins University Press. ISBN 978-0-8018-1990-2. {{cite book}}: Invalid |ref=harv (help)
• Pedersen, Olaf (1993). Early Physics and Astronomy: A Historical Introduction (2nd ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-40340-5. {{cite book}}: Invalid |ref=harv (help)
• Revello, Manuela (2013). "Sole, luna ed eclissi in Omero", in TECHNAI 4. Pisa-Roma: Fabrizio Serra editore. pp. 13–32. {{cite book}}: Invalid |ref=harv (help)
• Toomer, Gerald J. (1998). Ptolemy's Almagest. Princeton: Princeton University Press. ISBN 978-0-691-00260-6. {{cite book}}: Invalid |ref=harv (help)
• Bowler, Peter J., and Iwan Rhys Morus. Making Modern Science: A Historical Survey. Chicago, IL: Univ. of Chicago Press, 2010.

External links

• Almagest Planetary Model Animations
• MacTutor History of Mathematics Archive
• Greek Astronomy