Gamma (eclipse)

Gamma of a central total eclipse. This illustrates solar eclipse gamma: The red line shows the least distance from the center of the Earth, in this case approximately 75% of radius of the Earth. Because the umbra passes north of the Earth's center, gamma in this example is +0.75.

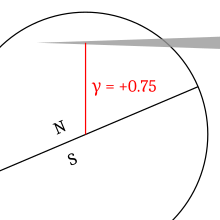
Gamma (denoted as γ) of an eclipse describes how centrally the shadow of the Moon or Earth strikes the other body. This distance, measured at the moment when the axis of the shadow cone passes closest to the center of the Earth or Moon, is stated as a fraction of the equatorial radius of the Earth or Moon.

Sign

The sign of gamma defines, for a solar eclipse, if the axis of the shadow passes north or south of the center of the Earth; a positive value means north. The Earth is defined as that half which is exposed to the Sun (this changes with the seasons and is not related directly to the Earth's poles or equator; thus, the Earth's center is wherever the Sun is directly overhead).

For a lunar eclipse, it defines whether the axis of the Earth's shadow passes north or south of the Moon; a positive value means south.

Gamma changes monotonically throughout any single saros series. The change in gamma is larger when Earth is near its aphelion (June to July) than when it is near perihelion (December to January). For odd numbered series (ascending node for solar eclipses and descending node for lunar eclipses), gamma decreases for solar eclipses and gamma increases for lunar eclipses, while for even numbered series (descending node for solar eclipses and ascending node for lunar eclipses), gamma increases for solar eclipses and gamma decreases for lunar eclipses. This simple rule describes the current behavior of gamma, but this has not always been the case. The eccentricity of Earth's orbit is presently 0.0167, and is slowly decreasing. It was 0.0181 in the year -2000 and will be 0.0163 in +3000. In the past, when the eccentricity was larger, there were saros series in which the trend in gamma reversed for one or more saros cycles before resuming its original direction. These instances occur near perihelion when the Sun's apparent motion is highest and may, in fact, overtake the eastward shift of the node. The resulting effect is a relative shift west of the node after one saros cycle instead of the usual eastward shift. Consequently, gamma reverses direction.

Limiting cases for solar eclipses on the earth

The absolute value of gamma (denoted as |γ|) allows us to distinguish different kinds of solar eclipses from the earth:

If the Earth were a sphere, the limit for a central eclipse would be 1.0, but because of the oblateness of the Earth (which causes the distance between the Earth's north and south poles to be slightly shorter than if the were perfectly spherical), it is 0.9972.

• If |γ| is 0, the axis of the shadow cone is exactly between the northern and southern halves of the sunlit side of the Earth when it passes over the center.
• If |γ| is lower than 0.9972, the eclipse is central. The axis of the shadow cone strikes the Earth and there are locations on Earth, where the Moon can be seen centered in front of the Sun. Central eclipses can be total or annular (if the tip of the umbra only barely reaches the surface of the Earth, the type can change during the eclipse from annular to total and/or vice versa; this is called a hybrid eclipse).
• If |γ| is between 0.9677826 and 0.9972, the eclipse is central (one limit), because one edge misses the Earth.
• If |γ| is between 0.9972 and 1.0266174, the axis of the shadow cone misses Earth, but, because the umbra or antumbra has a nonzero width, part of the umbra or antumbra may touch down in the polar regions of the Earth. This is called a non-central total or annular eclipse.
• If |γ| is between 0.9972 and 1.0266174 and the special circumstances mentioned above do not occur, or if |γ| is greater than 1.0266174 but less than approximately 1.55, the eclipse is partial; the Earth traverses only the penumbra.
• If |γ| exceeds approximately 1.55 (1.53 for total solar eclipses and 1.57 for annular solar eclipses when the gamma is 0.9972 or smaller), the shadow cone misses the Earth completely, and no eclipse occurs.

The Solar eclipse of April 29, 2014, with a gamma of -0.99996, is an example of the special case of a non-central annular eclipse. The axis of the shadow cone barely missed Earth's south pole. Thus, no central line could be specified for the zone of annular visibility.

The next non-central eclipse in 21st century is total solar eclipse of April 9, 2043.

Limiting cases for lunar eclipses on the moon with respect to Earth's umbral and penumbral shadows

There are three types of lunar eclipses:

• Penumbral Lunar Eclipse = The Moon passes through Earth's penumbra, but the Earth's umbra misses the Moon.
• Partial Lunar Eclipse = The Moon passes through Earth's umbra, but not completely.
• Total Lunar Eclipse = The Moon passes through Earth's umbra, completely.

The gamma is the limit of:

• If |γ| is 0, the Moon's center passes exactly through the axis of the Earth's umbra.

• If |γ| is lower than 0.2725, this lunar eclipse is central.

• If |γ| is between 0.2725 and 0.47, this lunar eclipse is total.

• If |γ| is between 0.43 and 0.987, this lunar eclipse is partial with a penumbral magnitude greater than 1.

• If |γ| is between 0.987 and 1.0266174, this lunar eclipse is total penumbral or partial with a penumbral magnitude less than 1.

• If |γ| is between 1.0266174 and approximately 1.55, this lunar eclipse is penumbral with penumbral magnitude less than 1, the Moon traverses only the Earth's penumbra.

• If |γ| exceeds approximately 1.55, the Earth's penumbra misses the Moon completely, and no eclipse occurs.