6
| ||||
|---|---|---|---|---|
| Cardinal | six | |||
| Ordinal | 6th (sixth) | |||
| Numeral system | senary | |||
| Factorization | 2 × 3 | |||
| Divisors | 1, 2, 3, 6 | |||
| Greek numeral | Ϛ´ | |||
| Roman numeral | VI, vi, ↅ | |||
| Greek prefix | hexa-/hex- | |||
| Latin prefix | sexa-/sex- | |||
| Binary | 1102 | |||
| Ternary | 203 | |||
| Senary | 106 | |||
| Octal | 68 | |||
| Duodecimal | 612 | |||
| Hexadecimal | 616 | |||
| Greek | στ (or ΣΤ or ς) | |||
| Arabic, Kurdish, Sindhi, Urdu | ٦ | |||
| Persian | ۶ | |||
| Amharic | ፮ | |||
| Bengali | ৬ | |||
| Chinese numeral | 六,陸 | |||
| Devanāgarī | ६ | |||
| Gujarati | ૬ | |||
| Hebrew | ו | |||
| Khmer | ៦ | |||
| Thai | ๖ | |||
| Telugu | ౬ | |||
| Tamil | ௬ | |||
| Saraiki | ٦ | |||
| Malayalam | ൬ | |||
| Armenian | Զ | |||
| Babylonian numeral | 𒐚 | |||
| Egyptian hieroglyph | 𓏿 | |||
| Morse code | _ .... | |||
6 (six) is the natural number following 5 and preceding 7. It is a composite number and the smallest perfect number.[1]
In mathematics
[edit]Six is the smallest positive integer which is neither a square number nor a prime number. It is the second smallest composite number after four, equal to the sum and the product of its three proper divisors (1, 2 and 3).[1] As such, six is the only number that is both the sum and product of three consecutive positive numbers. 6 is the smallest perfect number, which are numbers that are equal to their aliquot sum, or sum of their proper divisors.[1][2] It is the largest of the four all-Harshad numbers (1, 2, 4, and 6),[3] where it represents the sum between the first prime and composite, 2 and 4.
6 is a pronic number and the only semiprime to be.[4] It is the first discrete biprime (2 × 3)[5] which makes it the first member of the (2 × q) discrete biprime family, where q is a higher prime. All primes above 3 are of the form 6n ± 1 for n ≥ 1.
As a perfect number:
- 6 is related to the Mersenne prime 3, since 21(22 – 1) = 6. (The next perfect number is 28.)
- 6 is the only even perfect number that is not the sum of successive odd cubes.[6]
- 6 is the root of the 6-aliquot tree, and is itself the aliquot sum of only one other number; the square number 25.
Six is the first unitary perfect number, since it is the sum of its positive proper unitary divisors, without including itself. Only five such numbers are known to exist; sixty (10 × 6) and ninety (15 × 6) are the next two.[7]
It is the first primitive pseudoperfect number,[8] and all integers that are multiples of 6 are pseudoperfect (all multiples of a perfect number are pseudoperfect); six is also the smallest Granville number, or -perfect number.[9]
Unrelated to 6's being a perfect number, a Golomb ruler of length 6 is a "perfect ruler".[10] Six is a congruent number.[11]
6 is the second primary pseudoperfect number,[12] and harmonic divisor number.[13] It is also the second superior highly composite number,[14] and the last to also be a primorial.
There are 6 non-equivalent ways in which 100 can be expressed as the sum of two prime numbers: (3 + 97), (11 + 89), (17 + 83), (29 + 71), (41 + 59) and (47 + 53).[15]
There is not a prime such that the multiplicative order of 2 modulo is 6, that is, By Zsigmondy's theorem, if is a natural number that is not 1 or 6, then there is a prime such that . See A112927 for such .
The ring of integer of the sixth cyclotomic field Q(ζ6), which is called Eisenstein integer, has 6 units: ±1, ±ω, ±ω2, where .
The six exponentials theorem guarantees (given the right conditions on the exponents) the transcendence of at least one of a set of exponentials.[16]
There are six basic trigonometric functions: sin, cos, sec, csc, tan, and cot.[17]
The smallest non-abelian group is the symmetric group which has 3! = 6 elements.[1]
Six is a triangular number[18] and so is its square (36). It is the first octahedral number, preceding 19.[19]
A six-sided polygon is a hexagon,[1] one of the three regular polygons capable of tiling the plane. Figurate numbers representing hexagons (including six) are called hexagonal numbers. Because 6 is the product of a power of 2 (namely 21) with nothing but distinct Fermat primes (specifically 3), a regular hexagon is a constructible polygon with a compass and straightedge alone. A hexagram is a six-pointed geometric star figure (with the Schläfli symbol {6/2}, 2{3}, or {{3}}).
Six similar coins can be arranged around a central coin of the same radius so that each coin makes contact with the central one (and touches both its neighbors without a gap), but seven cannot be so arranged. This makes 6 the answer to the two-dimensional kissing number problem.[20] The densest sphere packing of the plane is obtained by extending this pattern to the hexagonal lattice in which each circle touches just six others.
There is only one non-trivial magic hexagon: it is of order-3 and made of nineteen cells, with a magic constant of 38. All rows and columns in a 6 × 6 magic square collectively generate a magic sum of 666 (which is doubly triangular). On the other hand, Graeco-Latin squares with order 6 do not exist; if is a natural number that is not 2 or 6, then there is a Graeco-Latin square of order .[21]
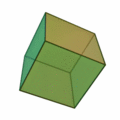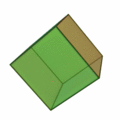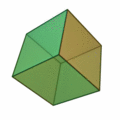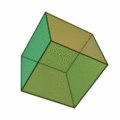
The cube is one of five Platonic solids, with a total of six squares as faces. It is the only regular polyhedron that can generate a uniform honeycomb on its own, which is also self-dual. The cuboctahedron, which is an Archimedean solid that is one of two quasiregular polyhedra, has eight triangles and six squares as faces. Inside, its vertex arrangement can be interpreted as three hexagons that intersect to form an equatorial hexagonal hemi-face, by-which the cuboctahedron is dissected into triangular cupolas. This solid is also the only polyhedron with radial equilateral symmetry, where its edges and long radii are of equal length; its one of only four polytopes with this property — the others are the hexagon, the tesseract (as the four-dimensional analogue of the cube), and the 24-cell. Only six polygons are faces of non-prismatic uniform polyhedra such as the Platonic solids or the Archimedean solids: the triangle, the square, the pentagon, the hexagon, the octagon, and the decagon. If self-dual images of the tetrahedron are considered distinct, then there are a total of six regular polyhedra that are formed by three different Weyl groups in the third dimension (based on tetrahedral, octahedral and icosahedral symmetries).
How closely the shape of an object resembles that of a perfect sphere is called its sphericity, calculated by:[22]
where is the surface area of the sphere, the volume of the object, and the surface area of the object.
In four dimensions, there are a total of six convex regular polytopes: the 5-cell, 8-cell, 16-cell, 24-cell, 120-cell, and 600-cell.
, with 720 = 6! elements, is the only finite symmetric group which has an outer automorphism. This automorphism allows us to construct a number of exceptional mathematical objects such as the S(5,6,12) Steiner system, the projective plane of order 4, the four-dimensional 5-cell, and the Hoffman-Singleton graph. A closely related result is the following theorem: 6 is the only natural number for which there is a construction of isomorphic objects on an -set , invariant under all permutations of , but not naturally in one-to-one correspondence with the elements of . This can also be expressed category theoretically: consider the category whose objects are the element sets and whose arrows are the bijections between the sets. This category has a non-trivial functor to itself only for .
In the classification of finite simple groups, twenty of twenty-six sporadic groups in the happy family are part of three families of groups which divide the order of the friendly giant, the largest sporadic group: five first generation Mathieu groups, seven second generation subquotients of the Leech lattice, and eight third generation subgroups of the friendly giant. The remaining six sporadic groups do not divide the order of the friendly giant, which are termed the pariahs (Ly, O'N, Ru, J4, J3, and J1).[23]
List of basic calculations
[edit]| Multiplication | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 25 | 50 | 100 | 1000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 × x | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | 78 | 84 | 90 | 96 | 102 | 108 | 114 | 120 | 150 | 300 | 600 | 6000 |
| Division | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 ÷ x | 6 | 3 | 2 | 1.5 | 1.2 | 1 | 0.857142 | 0.75 | 0.6 | 0.6 | 0.54 | 0.5 | 0.461538 | 0.428571 | 0.4 | |
| x ÷ 6 | 0.16 | 0.3 | 0.5 | 0.6 | 0.83 | 1 | 1.16 | 1.3 | 1.5 | 1.6 | 1.83 | 2 | 2.16 | 2.3 | 2.5 |
| Exponentiation | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6x | 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 | 362797056 | 2176782336 | 13060694016 | |
| x6 | 1 | 64 | 729 | 4096 | 15625 | 46656 | 117649 | 262144 | 531441 | 1000000 | 1771561 | 2985984 | 4826809 |
Greek and Latin word parts
[edit]Hexa
[edit]Hexa is classical Greek for "six".[1] Thus:
- "Hexadecimal" combines hexa- with the Latinate decimal to name a number base of 16[24]
- A hexagon is a regular polygon with six sides[25]
- L'Hexagone is a French nickname for the continental part of Metropolitan France for its resemblance to a regular hexagon
- A hexahedron is a polyhedron with six faces, with a cube being a special case[26]
- Hexameter is a poetic form consisting of six feet per line
- A "hex nut" is a nut with six sides, and a hex bolt has a six-sided head
- The prefix "hexa-" also occurs in the systematic name of many chemical compounds, such as hexane which has 6 carbon atoms (C6H14).
The prefix sex-
[edit]Sex- is a Latin prefix meaning "six".[1] Thus:
- Senary is the ordinal adjective meaning "sixth"[27]
- People with sexdactyly have six fingers on each hand
- The measuring instrument called a sextant got its name because its shape forms one-sixth of a whole circle
- A group of six musicians is called a sextet
- Six babies delivered in one birth are sextuplets
- Sexy prime pairs – Prime pairs differing by six are sexy, because sex is the Latin word for six.[28][29]
The SI prefix for 10006 is exa- (E), and for its reciprocal atto- (a).
Evolution of the Hindu-Arabic digit
[edit]

The evolution of our modern digit 6 appears rather simple when compared with the other digits. The modern 6 can be traced back to the Brahmi numerals of India, which are first known from the Edicts of Ashoka c. 250 BCE.[30][31][32][33] It was written in one stroke like a cursive lowercase e rotated 90 degrees clockwise. Gradually, the upper part of the stroke (above the central squiggle) became more curved, while the lower part of the stroke (below the central squiggle) became straighter. The Arabs dropped the part of the stroke below the squiggle. From there, the European evolution to our modern 6 was very straightforward, aside from a flirtation with a glyph that looked more like an uppercase G.[34]
On the seven-segment displays of calculators and watches, 6 is usually written with six segments. Some historical calculator models use just five segments for the 6, by omitting the top horizontal bar. This glyph variant has not caught on; for calculators that can display results in hexadecimal, a 6 that looks like a "b" is not practical.
Just as in most modern typefaces, in typefaces with text figures the character for the digit 6 usually has an ascender, as, for example, in ![]() .[35]
.[35]
This digit resembles an inverted 9. To disambiguate the two on objects and documents that can be inverted, the 6 has often been underlined, both in handwriting and on printed labels.
In music
[edit]
In artists
[edit]- Les Six ("The Six" in English) was a group consisting of the French composers Georges Auric, Louis Durey, Arthur Honegger, Darius Milhaud, Francis Poulenc and Germaine Tailleferre in the 1920s[36]
- Bands with the number six in their name include Six Organs of Admittance,[37] 6 O'Clock Saints, Electric Six,[38] Eve 6, Los Xey (sei is Basque for "six"), Out On Blue Six, Six In Six, Sixpence None the Richer,[39] Slant 6,[40] Vanity 6, and You Me At Six[41]
- #6 is the pseudonym of American musician Shawn Crahan, when performing with the band Slipknot
In instruments
[edit]- A standard guitar has six strings[42]
- Most woodwind instruments have six basic holes or keys (e.g., bassoon, clarinet, pennywhistle, saxophone); these holes or keys are usually not given numbers or letters in the fingering charts
In music theory
[edit]In works
[edit]- "Six geese a-laying" were given as a present on the sixth day in the popular Christmas carol, "The Twelve Days of Christmas".[45]
- Divided in six arias, Hexachordum Apollinis is generally regarded as one of the pinnacles of Johann Pachelbel's oeuvre.[46]
- The theme of the sixth album by Dream Theater, Six Degrees of Inner Turbulence, was the number six: the album has six songs, and the sixth song—that is, the complete second disc—explores the stories of six individuals suffering from various mental illnesses.[47]
- Aristotle gave six elements of tragedy, the first of which is Mythos.[48]
In religion
[edit]
Judaism
[edit]- Six points on a Star of David[49]
- Six orders of the Mishnah[50]
- Six symbolic foods placed on the Passover Seder Plate[51]
- God took six days to create the world in the Old Testament Book of Genesis;[52] humankind was created on day 6. In the City of God, Augustine of Hippo suggested (book 11, chapter 30) that God's creation of the world took six days because 6 is a perfect number.[53]
- The Jewish holiday of Shavuot starts on the sixth day of the Hebrew month of Sivan[54]
- Seraphs have six wings.[55]
Islam
[edit]- There are Six articles of faith[56]
- Six points on a Seal of Solomon
- Fasting six days of Shawwal, together with the month of Ramadan, is equivalent to fasting the whole year[57]
- The heavens and earth were created in six days according to the Quran:[58]
Indeed, We created the heavens and the earth and everything in between in six Days,1 and We were not ˹even˺ touched with fatigue.2
Note 1: The word day is not always used in the Quran to mean a 24-hour period. According to Surah Al-Hajj (The Pilgrimage):47, a heavenly Day is 1000 years of our time. The Day of Judgment will be 50,000 years of our time - Surah Al-Maarij (The Ascending Stairways):4. Hence, the six Days of creation refer to six eons of time, known only by Allah.
Note 2: Some Islamic scholars believe this verse comes in response to Exodus 31:17, which says, "The Lord made the heavens and the earth in six days, but on the seventh day He rested and was refreshed."
Others
[edit]- In Hindu theology, a trasarenu is the combination of six celestial paramānus (atoms).
- In Taoism:
- Six Lines of a Hexagram
- Six Ministries of Huang Di[59]
In science
[edit]Astronomy
[edit]- Messier object M6, a magnitude 4.5 open cluster in the constellation Scorpius, also known as the Butterfly Cluster[60]
- The New General Catalogue object NGC 6, a spiral galaxy in the constellation Andromeda
- The Roman numeral VI:
- Stands for subdwarfs in the Yerkes spectral classification scheme
- (Usually) stands for the sixth-discovered satellite of a planet or minor planet (e.g. Jupiter VI)
- 6 Hebe
Biology
[edit]
- The cells of a beehive are six-sided.[61]
- Insects have six legs (see Hexapoda).[62]
- Six kingdoms in the taxonomic rank below domain (biology); Animalia, Plantae, Fungi, Protista, Archaea/Archaeabacteria, and Bacteria/Eubacteria. See Kingdom (biology).[63]
- The six elements most common in biomolecules are called the CHNOPS elements; the letters stand for the chemical abbreviations of carbon, hydrogen, nitrogen, oxygen, phosphorus, and sulfur. See CHON.[64]
Chemistry
[edit]
- A benzene molecule has a ring of six carbon atoms.[65]
- 6 is the atomic number of carbon.[66]
- The sixfold symmetry of snowflakes arises from the hexagonal crystal structure of ordinary ice.[67]
- A hexamer is an oligomer made of six subunits.
Medicine
[edit]- There are six tastes in traditional Indian medicine (Ayurveda): sweet, sour, salty, bitter, pungent, and astringent. These tastes are used to suggest a diet based on the symptoms of the body.[68]
- Phase 6 is one of six pandemic influenza phases.[69]
Physics
[edit]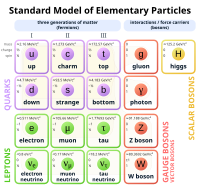
- In the Standard Model of particle physics, there are six types of quarks and six types of leptons.[70]
- In statistical mechanics, the six-vertex model has six possible configurations of arrows at each vertex[71]
- There are six colors in the RGB color wheel: (primary) red, blue, green, (secondary) cyan, magenta, and yellow. (See Tertiary color)[72]
- In three-dimensional Euclidean space, there are six unknown support reactions for a statically determinate structure: one force in each of the three dimensions, and one moment through each of three possible orthogonal planes.
In sports
[edit]- The Original Six teams in the National Hockey League are Toronto, Chicago, Montreal, New York, Boston, and Detroit.[73] They are the oldest remaining teams in the league, though not necessarily the first six; they comprised the entire league from 1942 to 1967.
- Number of players:
- In association football (soccer), the number of substitutes combined by both teams, that are allowed in the game.
- In box lacrosse, the number of players per team, including the goaltender, that are on the floor at any one time, excluding penalty situations.[74]
- In ice hockey, the number of players per team, including the goaltender, that are on the ice at any one time during regulation play, excluding penalty situations. (Some leagues reduce the number of players on the ice during overtime.)[75]
- In volleyball:
- Six players from each team on each side play against each other.[76]
- Standard rules only allow six total substitutions per team per set. (Substitutions involving the libero, a defensive specialist who can only play in the back row, are not counted against this limit.)
- Six-man football is a variant of American or Canadian football, played by smaller schools with insufficient enrollment to field the traditional 11-man (American) or 12-man (Canadian) squad.[77]
- Scoring:
- In both American and Canadian football, 6 points are awarded for a touchdown.[78]
- In Australian rules football, six points are awarded for a goal, scored when a kicked ball passes between the defending team's two inner goalposts without having been touched by another player.
- In cricket, six runs are scored for the batting team when the ball is hit to the boundary or the ground beyond it without having touched the ground in the field.
- In basketball, the ball used for women's full-court competitions is designated "size 6".[79]
- In pool and snooker one its table contains six pockets.
- In most rugby league competitions (but not the Super League, which uses static squad numbering), the jersey number 6 is worn by the starting five-eighth (Southern Hemisphere term) or stand-off (Northern Hemisphere term).
- In rugby union, the starting blindside flanker wears jersey number 6. (Some teams use "left" and "right" flankers instead of "openside" and "blindside", with 6 being worn by the starting left flanker.)[80]
In technology
[edit]
- On most phones, the 6 key is associated with the letters M, N, and O, but on the BlackBerry Pearl it is the key for J and K, and on the BlackBerry 8700 series and Curve 8900 with full keyboard, it is the key for F
- The "6-meter band" in amateur radio includes the frequencies from 50 to 54 MHz
- 6 is the resin identification code used in recycling to identify polystyrene[81]
In calendars
[edit]- In the ancient Roman calendar, Sextilis was the sixth month. After the Julian reform, June became the sixth month and Sextilis was renamed August[82]
- Sextidi was the sixth day of the décade in the French Revolutionary calendar[83]
In the arts and entertainment
[edit]Games
[edit]- The number of sides on a cube, hence the highest number on a standard die[84]
- The six-sided tiles on a hex grid are used in many tabletop and board games.
- The highest number on one end of a standard domino
Literature
[edit]- The Power of Six is a book written by Pittacus Lore, and the second in the Lorien Legacies series.[85]
- Number 6 is a character in the book series Lorien Legacies.
TV
[edit]- Number Six (Tricia Helfer) is a family of fictional characters from the reimagined science fiction television series, Battlestar Galactica.
- Number 6, the main protagonist in The Prisoner played by Patrick McGoohan, and portrayed by Jim Caviezel in the remake.
- Six is a character in the television series Blossom played by Jenna von Oÿ.[86]
- Six is the nickname of Kal Varrik, a central character in the television series Dark Matter, played by Roger Cross.[87]
- Six is a History channel series that chronicles the operations and daily lives of SEAL Team Six.[88]
- Six Feet Under, an HBO series that ran from 2005 to 2011.[89]
Movies
[edit]- Number 6 (Teresa Palmer) is a character in the movie I Am Number Four (2011).[90]
- The 6th Day (2000), starring Arnold Schwarzenegger.[91]
- The Sixth Sense (1999), written and directed by M. Night Shyamalan and starring Haley Joel Osment and Bruce Willis.[92]
- Girl 6 (1996), directed by Spike Lee.[93]
Musicals
[edit]- Six is a modern retelling of the lives of the six wives of Henry VIII presented as a pop concert.[94]
Anthropology
[edit]- The name of the smallest group of Cub Scouts and Guiding's equivalent Brownies, traditionally consisting of six people and is led by a "sixer".
- A coffin is traditionally buried six feet under the ground; thus, the phrase "six feet under" means that a person (or thing, or concept) is dead[95]
- There are said to be no more than six degrees of separation between any two people on Earth.[96]
- In Western astrology, Virgo is the 6th astrological sign of the Zodiac[97]
- The Six Dynasties form part of Chinese history[98]
- Six is a lucky number in Chinese culture.[99]
- The Birmingham Six were a British miscarriage of justice, held in prison for 16 years.[100]
- "Six" is used as an informal slang term for the British Secret Intelligence Service, MI6.[101]
In other fields
[edit]
- Six-pack is a common form of packaging for six bottles or cans of drink (especially beer), and by extension, other assemblages of six items.[102] Also, six is half a dozen.
- The maximum number of dots in a braille cell.[103]
- Extrasensory perception is sometimes called the "sixth sense".[104]
- Six Flags is an American company running amusement parks and theme parks in the U.S., Canada, and Mexico.[105]
- In the U.S. Army "Six" as part of a radio call sign is used by the commanding officer of a unit, while subordinate platoon leaders usually go by "One".[106] (For a similar example see also: Rainbow Six.)
See also
[edit]References
[edit]- ^ a b c d e f g Weisstein, Eric W. "6". mathworld.wolfram.com. Retrieved 2020-08-03.
- ^ Higgins, Peter (2008). Number Story: From Counting to Cryptography. New York: Copernicus. p. 11. ISBN 978-1-84800-000-1.
- ^ Weisstein, Eric W. "Harshad Number". mathworld.wolfram.com. Retrieved 2020-08-03.
- ^ "Sloane's A002378: Pronic numbers". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2020-11-30.
- ^ Sloane, N. J. A. (ed.). "Sequence A001358 (Semiprimes (or biprimes): products of two primes.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2023-08-03.
- ^ David Wells, The Penguin Dictionary of Curious and Interesting Numbers. London: Penguin Books (1987): 67
- ^ Sloane, N. J. A. (ed.). "Sequence A002827 (Unitary perfect numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-01.
- ^ Sloane, N. J. A. (ed.). "Sequence A005835 (Pseudoperfect (or semiperfect) numbers n: some subset of the proper divisors of n sums to n.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2023-12-02.
- ^ "Granville number". OeisWiki. The Online Encyclopedia of Integer Sequences. Archived from the original on 29 March 2011. Retrieved 27 March 2011.
- ^ Bryan Bunch, The Kingdom of Infinite Number. New York: W. H. Freeman & Company (2000): 72
- ^ Sloane, N. J. A. (ed.). "Sequence A003273 (Congruent numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-01.
- ^ Sloane, N. J. A. (ed.). "Sequence A054377 (Primary pseudoperfect numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2018-11-02.
- ^ Sloane, N. J. A. (ed.). "Sequence A001599 (Harmonic or Ore numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-01.
- ^ Weisstein, Eric W. "Superior Highly Composite Number". mathworld.wolfram.com. Retrieved 2020-08-03.
- ^ Sloane, N. J. A. (ed.). "Sequence A065577 (Number of Goldbach partitions of 10^n)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2023-08-31.
- ^ Weisstein, Eric W. "Six Exponentials Theorem". mathworld.wolfram.com. Retrieved 2020-08-03.
- ^ Weisstein, Eric W. "Trigonometric Functions". mathworld.wolfram.com. Retrieved 2020-08-03.
- ^ Weisstein, Eric W. "Triangular Number". mathworld.wolfram.com. Retrieved 2020-08-03.
- ^ Sloane, N. J. A. (ed.). "Sequence A005900 (Octahedral numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-01.
- ^ Weisstein, Eric W. "Kissing Number". mathworld.wolfram.com. Retrieved 2020-08-03.
- ^ Weisstein, Eric W. "Euler's Graeco-Roman Squares Conjecture". mathworld.wolfram.com. Retrieved 2020-08-03.
- ^ Wadell, Hakon (1935). "Volume, Shape, and Roundness of Quartz Particles". The Journal of Geology. 43 (3): 250–280. Bibcode:1935JG.....43..250W. doi:10.1086/624298. JSTOR 30056250. S2CID 129624905.
- ^ Griess, Jr., Robert L. (1982). "The Friendly Giant" (PDF). Inventiones Mathematicae. 69: 91–96. Bibcode:1982InMat..69....1G. doi:10.1007/BF01389186. hdl:2027.42/46608. MR 0671653. S2CID 123597150. Zbl 0498.20013.
- ^ Weisstein, Eric W. "Hexadecimal". mathworld.wolfram.com. Retrieved 2020-08-03.
- ^ Weisstein, Eric W. "Hexagon". mathworld.wolfram.com. Retrieved 2020-08-03.
- ^ Weisstein, Eric W. "Hexahedron". mathworld.wolfram.com. Retrieved 2020-08-03.
- ^ Weisstein, Eric W. "Base". mathworld.wolfram.com. Retrieved 2020-08-03.
- ^ Chris K. Caldwell; G. L. Honaker Jr. (2009). Prime Curios!: The Dictionary of Prime Number Trivia. CreateSpace Independent Publishing Platform. p. 11. ISBN 978-1-4486-5170-2.
- ^ Weisstein, Eric W. "Sexy Primes". mathworld.wolfram.com. Retrieved 2020-08-03.
- ^ Hollingdale, Stuart (2014). Makers of Mathematics. Courier Corporation. pp. 95–96. ISBN 978-0-486-17450-1.
- ^ Publishing, Britannica Educational (2009). The Britannica Guide to Theories and Ideas That Changed the Modern World. Britannica Educational Publishing. p. 64. ISBN 978-1-61530-063-1.
- ^ Katz, Victor J.; Parshall, Karen Hunger (2014). Taming the Unknown: A History of Algebra from Antiquity to the Early Twentieth Century. Princeton University Press. p. 105. ISBN 978-1-4008-5052-5.
- ^ Pillis, John de (2002). 777 Mathematical Conversation Starters. MAA. p. 286. ISBN 978-0-88385-540-9.
- ^ Georges Ifrah, The Universal History of Numbers: From Prehistory to the Invention of the Computer transl. David Bellos et al. London: The Harvill Press (1998): 395, Fig. 24.66
- ^ Negru, John (1988). Computer Typesetting. Van Nostrand Reinhold. p. 59. ISBN 978-0-442-26696-7.
slight ascenders that rise above the cap height ( in 4 and 6 )
- ^ Auric, Georges; Durey, Louis; Honegger, Arthur; Milhaud, Darius; Poulenc, Francis; Tailleferre, Germaine (2014-08-20). Caramel Mou and Other Great Piano Works of "Les Six": Pieces by Auric, Durey, Honegger, Milhaud, Poulenc and Tailleferre (in French). Courier Corporation. ISBN 978-0-486-49340-4.
- ^ "Six Organs of Admittance". www.sixorgans.com. Retrieved 2020-08-03.
- ^ "Electric Six | Biography, Albums, Streaming Links". AllMusic. Retrieved 2020-08-03.
- ^ "Sixpence None The Richer". GRAMMY.com. 2020-05-19. Retrieved 2020-08-04.
- ^ "Slant 6 | Biography & History". AllMusic. Retrieved 2020-08-04.
- ^ "You Me at Six | Biography & History". AllMusic. Retrieved 2020-08-04.
- ^ "Definition of GUITAR". www.merriam-webster.com. Retrieved 2020-08-04.
- ^ D'Amante, Elvo (1994-01-01). Music Fundamentals: Pitch Structures and Rhythmic Design. Scarecrow Press. p. 194. ISBN 978-1-4616-6985-2.
The division of an octave into six equal parts is referred to as the whole-tone scale
- ^ Horsley, Charles Edward (1876). A Text Book of Harmony: For the Use of Schools and Students. Sampson Low, Marston, Searle, & Rivington. p. 4.
Like the Tritone, it contains six semitones
- ^ Tribble, Mimi (2004). 300 Ways to Make the Best Christmas Ever!: Decorations, Carols, Crafts & Recipes for Every Kind of Christmas Tradition. Sterling Publishing Company, Inc. p. 145. ISBN 978-1-4027-1685-0.
Six geese a-laying
- ^ Staines, Joe (2010-05-17). The Rough Guide to Classical Music. Penguin. p. 393. ISBN 978-1-4053-8321-9.
...the six arias with variations collected under the title Hexachordum Apollinis (1699)...
- ^ Hegarty, Paul; Halliwell, Martin (2011-06-23). Beyond and Before: Progressive Rock since the 1960s. Bloomsbury Publishing USA. p. 169. ISBN 978-1-4411-1480-8.
Six Degrees of Inner Turbulence
- ^ Curran, Angela (2015-10-05). Routledge Philosophy Guidebook to Aristotle and the Poetics. Routledge. p. 133. ISBN 978-1-317-67706-2.
THE SIX QUALITATIVE ELEMENTS OF TRAGEDY
- ^ Plaut, W. Gunther (1991). The Magen David: How the Six-pointed Star Became an Emblem for the Jewish People. B'nai B'rith Books. ISBN 978-0-910250-16-0.
How the Six-pointed Star Became an Emblem for the Jewish People
- ^ Lauterbach, Jacob Zallel (1916). Midrash and Mishnah: A Study in the Early History of the Halakah. Bloch. p. 9.
Six orders of Mishnah
- ^ Rosen, Ceil; Rosen, Moishe (2006-05-01). Christ in the Passover. Moody Publishers. p. 79. ISBN 978-1-57567-480-3.
Six symbolic foods
- ^ Repcheck, Jack (2008-12-15). The Man Who Found Time: James Hutton And The Discovery Of Earth's Antiquity. Basic Books. ISBN 978-0-7867-4399-5.
it actually took only six days to create the earth
- ^ "CHURCH FATHERS: City of God, Book XI (St. Augustine)". www.newadvent.org. Retrieved 2020-08-04.
These works are recorded to have been completed in six days (the same day being six times repeated), because six is a perfect number
- ^ Grossman, Grace Cohen; Ahlborn, Richard E.; Institution, Smithsonian (1997). Judaica at the Smithsonian: Cultural Politics as Cultural Model. Smithsonian Institution Press. p. 228.
Shavuot falls on the sixth day of the Hebrew month of Sivan
- ^ Robertson, William Archibald Scott (1880). The crypt of Canterbury cathedral; its architecture, its history, and its frescoes. Mitchell & Hughes. p. 91.
...but seraphs, with six wings
- ^ Shapera, Paul M. (2009-08-15). Iran's Religious Leaders. The Rosen Publishing Group, Inc. p. 10. ISBN 978-1-4358-5283-9.
Islam has six articles of faith
- ^ Algül, Hüseyin (2005). The Blessed Days and Nights of the Islamic Year. Tughra Books. p. 65. ISBN 978-1-932099-93-5.
...it was blessed to fast for six days in the month of Shawwal...
- ^ "Surah Qaf - 38". Quran.com. Retrieved 2023-08-28.
- ^ Bary, William Theodore De; DeBary, William T.; Chan, Wing-tsit; Lufrano, Richard; Ching, Julia; Johnson, David; Liu, Kwang-Ching; Mungello, David (1999). Sources of Chinese Tradition. Columbia University Press. ISBN 978-0-231-11270-3.
...and the Six Ministries were made...
- ^ Rhoads, Samuel E. (1996). The Sky Tonight: A Guided Tour of the Stars Over Hawaiʻi. Bishop Museum Press. ISBN 978-0-930897-93-2.
Three Messier objects are visible in this part of the sky : M6, M7 and M8 .
- ^ Sedgwick, Marcus (2011-07-05). White Crow. Roaring Brook Press. p. 145. ISBN 978-1-4299-7634-3.
The cells of honeycombs are six-sided because a hexagon is the most material-efficient tessellation
- ^ Parker, Steve (2005). Ant Lions, Wasps & Other Insects. Capstone. p. 16. ISBN 978-0-7565-1250-7.
Insects have six legs each...
- ^ Pendarvis, Murray P.; Crawley, John L. (2019-02-01). Exploring Biology in the Laboratory: Core Concepts. Morton Publishing Company. p. 10. ISBN 978-1-61731-899-3.
...presently at least six kingdoms are recognized;
- ^ Mader, Sylvia S. (2004). Biology. McGraw-Hill. p. 20. ISBN 978-0-07-291934-9.
The acronym CHNOPS helps us remember these six elements
- ^ Dufour, Fritz (2018-09-19). The Realities of Reality - Part II: Making Sense of Why Modern Science Advances. Vol. 1. Fritz Dufour. p. 100.
The benzene molecule has its six carbon atoms in a ring
[self-published source?] - ^ Starr, Cecie; Evers, Christine (2012-05-10). Biology Today and Tomorrow without Physiology. Cengage Learning. p. 25. ISBN 978-1-133-36536-5.
For example, the atomic number of carbon is 6,
- ^ Webb, Stephen; Webb, Professor of Australian Studies Stephen (2004-05-25). Out of this World: Colliding Universes, Branes, Strings, and Other Wild Ideas of Modern Physics. Springer Science & Business Media. p. 16. ISBN 978-0-387-02930-6.
snowflake, with its familiar sixfold rotational symmetry
- ^ Woo, Teri Moser; Robinson, Marylou V. (2015-08-03). Pharmacotherapeutics For Advanced Practice Nurse Prescribers. F.A. Davis. p. 145. ISBN 978-0-8036-4581-3.
Ayurvedic herbology is based on the tridoshic theory that there exist six basic tastes
- ^ Pandemic Influenza Preparedness and Response Guidance for Healthcare Workers and Healthcare Employers. OSHA, U.S. Department of Labor. 2007. p. 8.
The WHO Plan describes six phases of increasing public health risk associated with the emergence of a new influenza
- ^ Sanghera, Paul (2011-03-08). Quantum Physics for Scientists and Technologists: Fundamental Principles and Applications for Biologists, Chemists, Computer Scientists, and Nanotechnologists. John Wiley & Sons. p. 64. ISBN 978-0-470-92269-9.
...there are six types of quarks and six types of leptons.
- ^ Jimbo, M.; Jimbo, Michio; Miwa, Tetsuji; Tsuchiya, Akihiro (1989). Integrable Systems in Quantum Field Theory and Statistical Mechanics. Academic Press. p. 588. ISBN 978-0-12-385342-4.
Allowed configurations in the six-vertex model and their statistical weights
- ^ Sloan, Robin James Stuart (2015-05-07). Virtual Character Design for Games and Interactive Media. CRC Press. p. 34. ISBN 978-1-4665-9820-1.
placing six primaries around the wheel in the following order: red, yellow, green, cyan, blue, magenta.
- ^ Bamford, Tab (2016-10-15). 100 Things Blackhawks Fans Should Know & Do Before They Die. Triumph Books. ISBN 978-1-63319-638-4.
the Original Six
- ^ Stillwell, Jim L. (1987). Making and Using Creative Play Equipment. Human Kinetics Publishers. p. 36. ISBN 978-0-87322-084-2.
Indoor Lacrosse . This is played with six players per team
- ^ Williams, Heather (2019). Hockey: A Guide for Players and Fans. Capstone. p. 16. ISBN 978-1-5435-7458-6.
There are six players per team on the ice at one time.
- ^ Sports, The National Alliance For Youth (2009-05-11). Coaching Volleyball For Dummies. John Wiley & Sons. p. 48. ISBN 978-0-470-53398-7.
In a regulation volleyball match with six players on each side of the court,
- ^ "sixmanfootball.com". www.sixmanfootball.com. Retrieved 2020-08-06.
- ^ "How Football Teams Can Score Points in Game Play". dummies. Retrieved 2020-08-06.
- ^ "Basketball Sizes Chart: What Size Ball Should a Player Use?". Basketball For Coaches. 2018-09-12. Retrieved 2020-08-06.
- ^ "Rugby flanker (#6 & #7): A position specific guide". Atrox Rugby. 2019-02-01. Retrieved 2020-08-06.
- ^ Stevens, E. S. (2002). Green Plastics: An Introduction to the New Science of Biodegradable Plastics. Princeton University Press. p. 45. ISBN 978-0-691-04967-0.
- ^ Bunson, Matthew (2014-05-14). Encyclopedia of the Roman Empire. Infobase Publishing. p. 90. ISBN 978-1-4381-1027-1.
Augustus was also originally called Sextilis, the sixth month.
- ^ Nicolas, Sir Nicholas Harris (1833). The Chronology of History: Containing Tables, Calculations and Statements, Indispensable for Ascertaining the Dates of Historical Events and of Public and Private Documents from the Earliest Period to the Present Time. Longham, Rees, Orme, Brown, Green, & Longman and John Taylor. p. 172.
SEXTIDI, or " Jour de la Révolution, "
- ^ Schumer, Peter D. (2004-02-11). Mathematical Journeys. John Wiley & Sons. p. 88. ISBN 978-0-471-22066-4.
Roll two dice, a standard six-sided die numbered 1 through 6
- ^ "'The Power of Six' trailer". EW.com. Retrieved 2020-08-06.
- ^ Terrace, Vincent (1993). Television Character and Story Facts: Over 110,000 Details from 1,008 Shows, 1945-1992. McFarland & Company. p. 54. ISBN 978-0-89950-891-7.
Every Monday Blossom and Six ( who also...
- ^ "Kal Varrick - Dark Matter". Universe Guide. Archived from the original on September 15, 2020. Retrieved 2020-08-06.
- ^ "Six: A Review". 2017-03-23. Retrieved 2020-08-06.
- ^ "The 100 Greatest TV Shows Of All Time". Empire. 2019-10-16. Retrieved 2020-08-06.
- ^ "Character profile for Number 6 from I Am Number Four (Lorien Legacies, #1) (page 1)". www.goodreads.com. Retrieved 2020-08-06.
- ^ The 6th Day (2000) - Roger Spottiswoode | Synopsis, Characteristics, Moods, Themes and Related | AllMovie, retrieved 2020-08-06
- ^ The Sixth Sense (1999) - M. Night Shyamalan | Synopsis, Characteristics, Moods, Themes and Related | AllMovie, retrieved 2020-08-06
- ^ Lee, Spike (1996-03-22), Girl 6 (Comedy, Drama), Theresa Randle, Isaiah Washington, Spike Lee, Jenifer Lewis, Fox Searchlight Pictures, 40 Acres & A Mule Filmworks, retrieved 2021-05-05
- ^ "Six the Musical". www.sixthemusical.com. Retrieved 2020-08-06.
- ^ Rimes, Wendy (2016-04-01). "The Reason Why The Dead Are Buried Six Feet Below The Ground". Elite Readers. Retrieved 2020-08-06.
- ^ "Six Degrees of Peggy Bacon". www.aaa.si.edu. 27 June 2012. Retrieved 2020-08-06.
- ^ "Virgo | constellation and astrological sign". Encyclopedia Britannica. Retrieved 2020-08-06.
- ^ Wilkinson, Endymion Porter; Wilkinson, Scholar and Diplomat (Eu Ambassador to China 1994-2001) Endymion (2000). Chinese History: A Manual. Harvard Univ Asia Center. p. 11. ISBN 978-0-674-00249-4.
{{cite book}}: CS1 maint: numeric names: authors list (link) - ^ "6 is a lucky number in Chinese culture - Google Search". www.google.com. Retrieved 2020-08-06.
Two of the luckiest numbers in China are '6' and '8'.
- ^ Peirce, Gareth (2011-03-12). "The Birmingham Six: Have we learned from our disgraceful past?". The Guardian. ISSN 0261-3077. Retrieved 2020-08-06.
- ^ Smith, Michael (2011-10-31). Six: The Real James Bonds 1909-1939. Biteback Publishing. ISBN 978-1-84954-264-7.
- ^ "Are Plastic Six-Pack Rings Still Ensnaring Wildlife?". Environment. 2018-09-19. Archived from the original on November 18, 2018. Retrieved 2020-08-06.
- ^ "What Is Braille? | American Foundation for the Blind". www.afb.org. Retrieved 2020-08-06.
- ^ Walker, Kathryn; Innes, Brian (2009). Mysteries of the Mind. Crabtree Publishing Company. p. 5. ISBN 978-0-7787-4149-7.
this is sometimes called a " sixth sense "
- ^ "Six Flags Reopens With Enhanced Safety Protocols | IAAPA". www.iaapa.org. 22 June 2020. Retrieved 2020-08-06.
- ^
- The number 6 is the opposite of number 4 in the amount of time remaining.
- The Odd Number 6, JA Todd, Math. Proc. Camb. Phil. Soc. 41 (1945) 66–68
- A Property of the Number Six, Chapter 6, P Cameron, JH v. Lint, Designs, Graphs, Codes and their Links ISBN 0-521-42385-6
- Wells, D. The Penguin Dictionary of Curious and Interesting Numbers London: Penguin Group. (1987): 67 - 69














